Insieme limitato in uno spazio metrico
Dato uno spazio metrico \((X, d)\), dove \(d\) è la metrica che misura la distanza tra punti, un insieme \(A \subseteq X\) si dice insieme limitato se esiste un numero positivo \(\mu > 0\) tale che la distanza \(d(x, y)\) tra qualsiasi coppia di punti \(x, y \in A\) è sempre minore o uguale a \(\mu\).
In pratica, tutti i punti di \(A\) si trovano entro una certa distanza massima \(\mu\) l'uno dall'altro.
Se l'intero insieme \(X\) è limitato rispetto alla metrica \(d\), allora si dice che \(d\) è una metrica limitata.
Questo significa che le distanze tra qualsiasi coppia di punti in \(X\) sono tutte inferiori a un certo valore massimo \(\mu\).
Nota. Se la metrica \(d\) è limitata, allora ogni sottoinsieme di \(X\) sarà automaticamente limitato, perché le distanze all'interno di qualsiasi sottoinsieme non possono superare quelle dell'insieme intero.
Un esempio pratico
Considero il piano cartesiano \(\mathbb{R}^2\) e la distanza euclidea come metrica.
La distanza tra due punti \((x_1, y_1)\) e \((x_2, y_2)\) è definita dalla formula:
$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
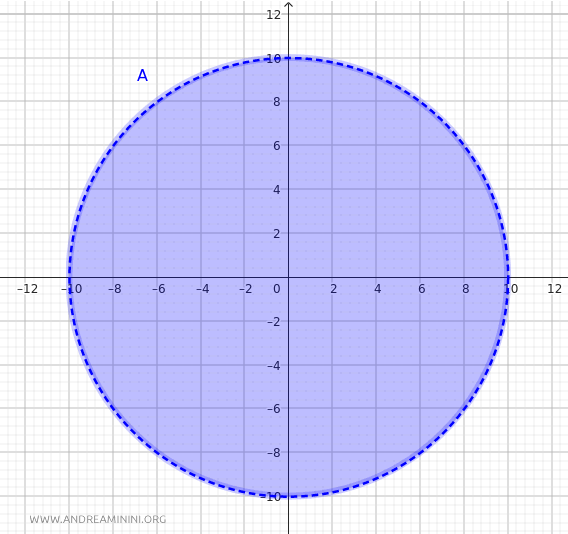
Ora considero il sottoinsieme \(A\) di \(\mathbb{R}^2\), definito come tutti i punti \((x, y)\) che soddisfano l'equazione del cerchio di raggio \(10\) con centro nell'origine. Questo insieme \(A\) è dato da:
$$ A = \{(x, y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 10^2\} $$
Un insieme è limitato se esiste un valore \(\mu > 0\) tale che per ogni coppia di punti \((x_1, y_1), (x_2, y_2) \in A\), si ha \(d((x_1, y_1), (x_2, y_2)) \leq \mu\).
In \(A\), i punti più distanti possibili sono due punti diametralmente opposti sul bordo del cerchio (ad esempio, \((10, 0)\) e \((-10, 0)\)).
La distanza tra questi due punti è:
$$ d((10, 0), (-10, 0)) = \sqrt{((-10) - 10)^2 + (0 - 0)^2} = \sqrt{(-20)^2} = 20 $$
La distanza massima tra due punti in \(A\) è \(20\).
Questo significa che non importa quali due punti scelgo dentro il cerchio, la loro distanza non sarà mai maggiore di \(20\).
Quindi, l'insieme \(A\) è limitato con \(\mu = 20\) perché tutti i punti \((x, y) \in A\) sono contenuti entro una distanza massima (il diametro del cerchio).
Il limite della metrica non influenza la topologia
E' interessante sottolineare che il limite di una metrica non influenza la topologia cioè, la struttura delle aperture e chiusure degli insiemi che induce.
Cos'è la topologia? La topologia è un modo per definire cosa significa che un insieme è "aperto" o "chiuso". Non dipende dai numeri precisi della metrica, ma dalla struttura generale dello spazio.
Quindi, anche se una metrica è infinita (non limitata), posso sempre trovare una nuova metrica equivalente, ma limitata, che mantiene esattamente la stessa topologia.
In altre parole: La limitatezza della metrica non cambia come sono definiti gli insiemi aperti o chiusi nello spazio.
Esempio
Per trasformare una metrica non limitata in una metrica limitata, posso utilizzare una funzione matematica che "riduce" le distanze grandi senza alterare la topologia dello spazio.
Un metodo molto comune consiste nel trasformare le distanze con una trasformazione come questa:
$$ d'(x, y) = \frac{d(x, y)}{1 + d(x, y)} $$
Come funziona questa trasformazione?
Quando la distanza \(d(x, y)\) è piccola, allora \(d'(x, y)\) sarà quasi uguale a \(d(x, y)\).
Per esempio, se \(d(x, y) = 1\), la nuova distanza sarà:
$$ d'(x, y) = \frac{1}{1 + 1} = 0.5 $$
Quando la distanza \(d(x, y)\) è molto grande (tende verso infinito), la nuova distanza \(d'(x, y)\) tende a 1.
Quindi, non importa quanto grandi siano le distanze originali, con questa trasformazione tutte le distanze vengono "comprese" tra 0 e 1.
Ad esempio, considero uno spazio metrico \((X, d)\), dove la distanza è data da \(d(x, y) = |x - y|\) (la distanza euclidea normale).
Questa metrica non è limitata, perché i punti \(x\) e \(y\) possono essere arbitrariamente distanti.
Applico la trasformazione:
$$ d'(x, y) = \frac{|x - y|}{1 + |x - y|} $$
Se \(x = 1\) e \(y = 2\), la distanza originale è \(d(1, 2) = 1\), mentre quella trasformata è:
$$ d'(1, 2) = \frac{1}{1 + 1} = 0.5 $$
Se \(x = 1\) e \(y = 1000\), la distanza originale è \(d(1, 1000) = 999\), ma la distanza trasformata diventa:
$$ d'(1, 1000) = \frac{999}{1 + 999} = 0.999 $$
Pertanto, tutte le distanze diventano limitate e comprese tra 0 e 1.
La struttura dello spazio non cambia perché gli insiemi aperti e chiusi definiti da \(d\) e da \(d'\) sono esattamente gli stessi.
E così via.
