Retta e piano incidenti o paralleli nello spazio
Nello spazio R3 una retta e un piano possono essere incidenti o paralleli (disgiunti o congiunti).
Equazioni parametriche
Se il piano e la retta sono definiti con le equazioni parametriche, per capire la loro posizione basta analizzare i vettori direttori.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} + t_2 \begin{pmatrix} l_3 \\ m_3 \\ n_3 \end{pmatrix} $$
Prendo i tre vettori direttori e li dispongo in colonna in una matrice.
Poi calcolo il rango della matrice.
$$ r_k \begin{pmatrix} l_1 & l_2 & l_3 \\ m_1 & m_2 & m_3 \\ n_1 & n_2 & n_3 \end{pmatrix} $$
Possono verificarsi due casi.
- r=3 Se il rango è uguale al numero dei vettori (r=3) i vettori sono linearmente indipendenti. Quindi, la retta e il piano sono incidenti.
- r<3 Se il rango è inferiore al numero dei vettori (r<3) i vettori sono linearmente dipendenti. Pertanto, la retta e il piano sono paralleli disgiunti o coincidenti.
Come capire se una retta e un piano paralleli sono disgiunti o coincidenti?
Per capire se la retta e il piano paralleli sono disgiunti o coincidenti, basta prendere un punto della retta e vedere se appartiene anche al piano.
Se sono coincidenti tutti i punti della retta appartengono anche al piano.
Viceversa, se sono disgiunti la retta non ha nessun punto in comune con il piano.
Esempio
Ho una retta e un piano
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} + t \begin{pmatrix} 4 \\ 2 \\ -1 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 7 \\ 6 \\ 5 \end{pmatrix} + t_1 \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix} $$
Calcolo il rango della matrice dei vettori direttori
$$ r_k \begin{pmatrix} 4 & 2 & -1 \\ 4 & -1 & 2 \\ 5 & 3 & 2 \end{pmatrix} =3 $$
I vettori sono linearmente indipendenti .
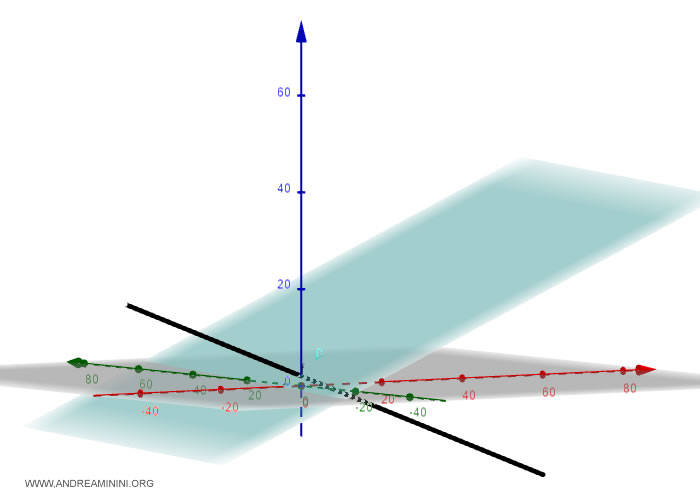
Quindi la retta è incidente al piano.
Equazioni cartesiane
Nel caso delle equazioni cartesiane, posso verificare la dipendenza lineare (o meno) dei vettori normali.
Scrivo la retta come intersezione di due piani.
$$ r: \begin{cases} a_1x + b_1y + c_1z +d_1 = 0 \\ a_2x + b_2y + c_2z +d_2 = 0 \end{cases} $$
$$ a_3x+b_3y+c_3z+d_3=0 $$
Prendo i vettori normali e li dispongo in riga in una matrice.
In questo modo tutti i coefficienti della variabile x sono in colonna, idem quelli della y e della z.
Poi calcolo il rango della matrice.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{pmatrix} $$
- r=3. Se il rango è uguale al numero dei vettori, i vettori sono linearmente indipendenti. Quindi la retta è incidente con il piano.
- r<3. Se il rango è inferiore al numero dei vettori, i vettori sono linearmente dipendenti. La retta è parallela al piano, giacente o disgiunta.
Come capire se la retta parallela al piano è giacente o disgiunta?
Per capirlo ricorro al teorema di Rouché-Capelli analizzando anche il rango della matrice A|B.
$$ r(A|B) \begin{pmatrix} a_1 & b_1 & c_1 & -d_1 \\ a_2 & b_2 & c_2 & -d_2 \\ a_3 & b_3 & c_3 & -d3 \end{pmatrix} $$
Se il rango r(A|B)=r(A)=2 allora il sistema ammette ∞n-r soluzioni e la retta è giacente sul piano.
Viceversa, se il sistema non ammette soluzioni la retta è disgiunta dal piano.
Esempio
Ho una retta e un piano
$$ r: \begin{cases} x + 2y + z -1 = 0 \\ 2x + 3y + z -3 = 0 \end{cases} $$
$$ x-y-2z-14=0 $$
Dispongo i coefficienti dei vettori normali in matrice.
Poi calcolo il rango.
$$ r_k \begin{pmatrix} 1 & 2 & 1 \\ 2 & 3 & 1 \\ 1 & -1 & -2 \end{pmatrix} = 2$$
Il rango è inferiore al numero dei vettori (r<3).
Quindi i vettori sono linearmente dipendenti. Il piano e la retta sono paralleli.
Per capire se sono coingiunti o disgiunti calcolo il rango della matrice A|B
$$ r(A|B) \begin{pmatrix} 1 & 2 & 1 & 1 \\ 2 & 3 & 1 & 3 \\ 1 & -1 & -2 & 14 \end{pmatrix} = 3$$
Il rango di A|B è diverso dal rango di A.
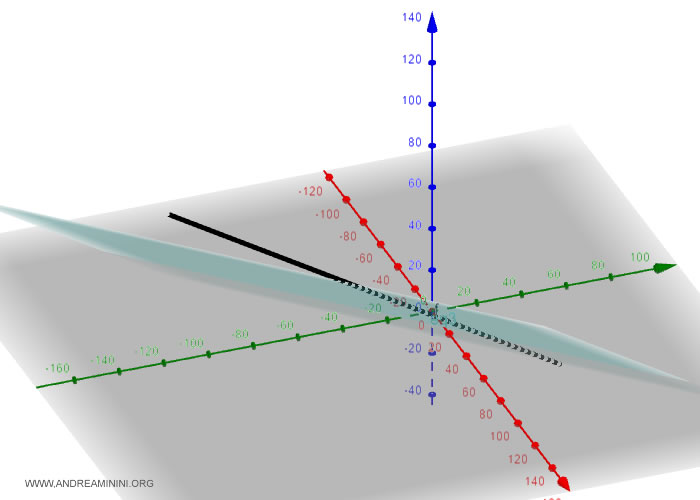
Pertanto, il sistema non soluzioni e la retta è parallela e disgiunta al piano.
E così via.
