Poliedro
Cos'è un poliedro
Un poliedro è l'intersezione di un numero finito di semispazi. Data una matrice Am,n, un vettore x di variabili e un vettore b, un poliedro è $$ Ax \le b $$
Come costruire un poliedro regolare
Ho una matrice 3x2 dei coefficienti
$$ A_{3,2} = \begin{pmatrix} 6 & 17 \\ -3 & -2 \\ 6 & -10 \end{pmatrix} $$
Un vettore x di variabili
$$ x = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} $$
Un vettore b di scalari.
$$ b = \begin{pmatrix} 51 \\ 3 \\ 15 \end{pmatrix} $$
Sostituisco i vettori nella formula del poliedro
$$ Ax \le b $$
$$ \begin{pmatrix} 6 & 17 \\ -3 & -2 \\ 6 & -10 \end{pmatrix} x \le b $$
$$ \begin{pmatrix} 6 & 17 \\ -3 & -2 \\ 6 & -10 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \le b $$
$$ \begin{pmatrix} 6 & 17 \\ -3 & -2 \\ 6 & -10 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \le \begin{pmatrix} 51 \\ 3 \\ 15 \end{pmatrix} $$
Svolgo il prodotto scalare della matrice per il vettore
$$ \begin{pmatrix} 6 x_1 + 17 x_2 \\ -3 x_1 -2 x_2 \\ 6 x_1 -10 x_2 \end{pmatrix} \le \begin{pmatrix} 51 \\ 3 \\ 15 \end{pmatrix} $$
Poi trasformo l'equazione vettoriale in un sistema di disequazioni.
Ogni disequazione è un semispazio.
$$ \begin{cases} 6 x_1 + 17 x_2 \le 51 \\ -3 x_1 -2 x_2 \le 3 \\ 6 x_1 -10 x_2 \le 15 \end{cases} $$
Ho così ottenuto il sistema di disequazioni che determina l'area del poliedro nel piano cartesiano.
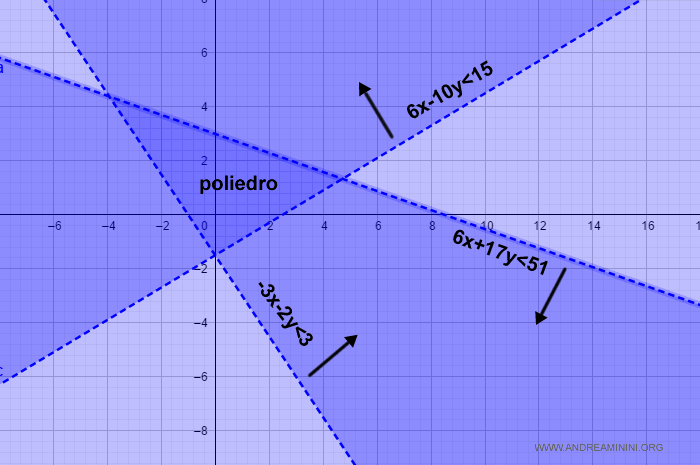
L'intersezione dei semispazi delinea l'area del poliedro.
In questo caso il poliedro è l'area triangolare al centro del diagramma cartesiano.
Nota. Per semplificare la spiegazione ho preferito disegnare una figura piana nello spazio bidimensionale. Tuttavia, il metodo può essere usato per costruire un solido nello spazio a tre dimensioni. E' più complesso ma il procedimento è sempre lo stesso. Occorre aggiungere un'ulteriore variabile (x,y,z) e molte più equazioni.
Se il poliedro è limitato è detto politopo.
Gli involucri del poliedro
Il poliedro è un insieme convesso perché, dati k vettori v e k scalari α si può determinare l'insieme affine, conico e convesso ( detti anche involucri o spazi ).
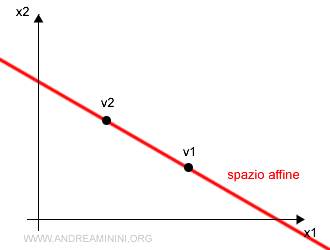
$$ Aff = \{ v=α_1v_1 +...+α_kv_k , \sum_{i=1}^k α_i = 1 \} $$
Esempio. Se i vettori sono solo due (k=2) lo spazio affine è la retta passante tra i due punti v1 e v2.
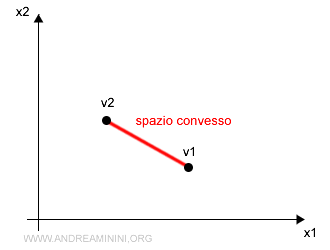
$$ Conv = \{ v=α_1v_1 +...+α_kv_k , \sum_{i=1}^k α_i = 1, α_1,...α_k \ge 0 \} $$
Esempio. Se i vettori sono solo due (k=2) lo spazio convesso è il segmento tra i due punti v1 e v2.
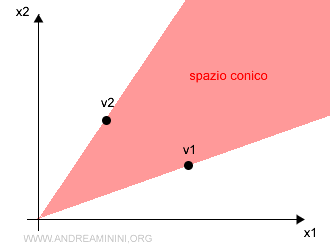
$$ Conico = \{ v=α_1v_1 +...+α_kv_k ,α_1,...α_k \ge 0 \} $$
Esempio. Se i vettori sono solo due (k=2) lo spazio conico è il più piccolo cono poliedrale centrato sull'origine che passa per i due punti v1 e v2.
I vertici del poliedro
Un vertice è un punto del poliedro P che non può essere ottenuto come combinazione lineare convessa di altri punti dell'insieme P.
La direzione del poliedro
La direzione del poliedro è un versore v delimitato tra due estremi che permette di determinare ogni punto x' di P dato un punto x0 di P e uno scalare qualsiasi non negativo α≥0. $$ x' = x_0 +α \cdot v $$
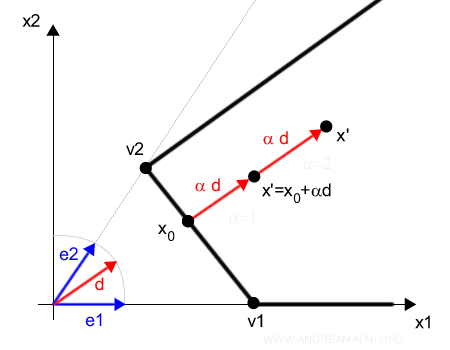
Le direzioni estreme e1 e e2 sono i versori individuati dai punti del poliedro P (v1 e v2) non esprimibili come combinazione conica di altri punti del poliedro.
Nota. Le direzione estreme possono essere gli assi del diagramma se le variabili x1 e x2 hanno il vincolo di non negatività, un lato oppure un vertice del poliedro.
Il sistema di disequazioni in forma compatta
Posso rappresentare il sistema di disequazioni del poliedro anche in una forma più compatta.
$$ Ax \le b $$
Dove A è la matrice dei coefficienti del sistema, x è il vettore delle variabili e b è il vettore dei termini noti.
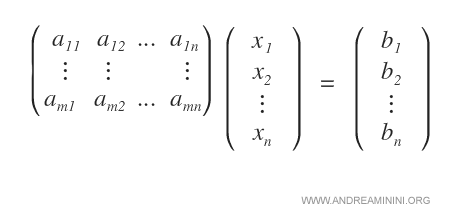
Il poliedro in forma standard
Un poliedro è in forma standard se il sistema di equazioni è Ax=b e l'insieme delle soluzioni è non negativo. $$ Ax = b $$
Come convertire il poliedro in forma standard?
Per trasformare il sistema di disequazioni del poliedro in forma standard effettuo queste operazioni
- Nelle disequazioni sostituisco ≥ con = aggiungendo al membro di sinistra una variabile ausiliare di scarto -s ( detta surplus ). $$ a_i^T x \ge b_i \rightarrow \begin{cases} a_i^T x = b_i + s_i \\ s_i \ge 0 \end{cases} \rightarrow \begin{cases} a_i^T x - s_i = b_i \\ s_i \ge 0 \end{cases} $$
- Nelle disequazioni sostituisco ≤ con = aggiungendo al membro di sinistra una variabile ausiliare di scarto +s ( detta slack ). $$ a_i^T x \le b_i \rightarrow \begin{cases} a_i^T x = b_i -s_i \\ s_i \ge 0 \end{cases} \rightarrow \begin{cases} a_i^T x +s_i = b_i \\ s_i \ge 0 \end{cases} $$
- Aggiungo un vincolo di non negatività sulle variabili x e s. $$ x,s ≥ 0 $$
- Se esistono dei vincoli con l'operatore x ≤ 0 li trasformo in ¬x ≥ 0 tramite la negazione della variabile $$ x \le 0 \rightarrow \overline{x} \ge 0 $$
- Se una variabile xj non ha vincoli di segno, la sostituisco con la differenza tra due variabili non negative xj+-xj-. $$ x_j = x_j^+ - x_j^- $$
Esempio
Il sistema di disequazioni iniziale
$$ \begin{cases} 6 x_1 + 17 x_2 \le 51 \\ -3 x_1 -2 x_2 \le 3 \\ 6 x_1 -10 x_2 \le 15 \end{cases} $$
per convertirlo in forma standard aggiungo le variabili ausiliarie di scarto
$$ \begin{cases} 6 x_1 + 17 x_2 + s_1 = 51 \\ -3 x_1 -2 x_2 + s_2 = 3 \\ 6 x_1 -10 x_2 + s_3 = 15 \\ s_1,s_2,s_3 \ge 0 \end{cases} $$
Nel sistema ci sono soltanto variabili libere.
Quindi le sostituisco con una differenza tra variabili non negative.
$$ \begin{cases} 6 (x_1^+ - x_1^-) + 17 (x_2^+ - x_2^-) + s_1 = 51 \\ -3 (x_1^+ - x_1^-) -2 (x_2^+ - x_2^-) + s_2 = 3 \\ 6 (x_1^+ - x_1^-) -10 (x_2^+ - x_2^-) + s_3 = 15 \\ s_1,s_2,s_3 \ge 0 \\ x_1^+, x_1^-,x_2^+,x_2^- \ge 0 \end{cases} $$
E' comunque preferibile usare altre incognite x invece di s
In questo modo posso considerare tutte le variabili in uno stesso vettore e il modello è elaborabile
$$ \begin{cases} 6 (x_1^+ - x_1^-) + 17 (x_2^+ - x_2^-) + x_3 = 51 \\ -3 (x_1^+ - x_1^-) -2 (x_2^+ - x_2^-) + x_4 = 3 \\ 6 (x_1^+ - x_1^-) -10 (x_2^+ - x_2^-) + x_5 = 15 \\ x_1^+, x_1^-,x_2^+,x_2^-, x_3,x_4,x_5 \ge 0 \end{cases} $$
Il risultato è il sistema del poliedro in forma standard.
Perché trasformare il poliedro in forma standard?
Un poliedro in forma standard non vuoto ha sempre un vertice.
E così via.
