L'iperpiano
Cos'è un iperpiano
Un iperpiano è un sottospazio lineare di dimensioni n-1 rispetto allo spazio che lo contiene.
Dato un vettore di coefficienti a, un vettore di variabili x e uno scalare b, l'iperpiano è un insieme determinato da
$$ I = \{ a^Tx = b \} $$
Un iperpiano è un insieme convesso.
Vuol dire che dati due punti qualsiasi dell'insieme, il segmento che li unisce appartiene sempre all'insieme.
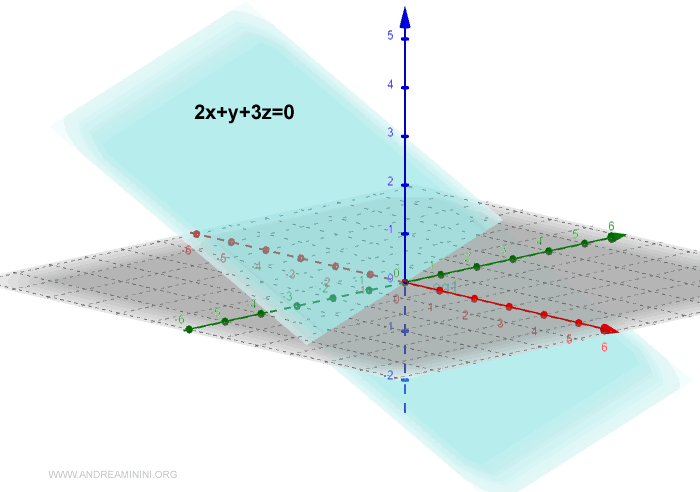
Nota. Nello spazio tridimensionale euclideo (x,y,z), gli iperpiani sono i piani a due dimensioni.
Lo spazio Rn viene suddiviso dall'iperpiano I in due semispazi S1 e S2.
$$ S_1 = \{ a^Tx \le b \} $$
$$ S_2 = \{ a^Tx \ge b \} $$
La prima combinazione lineare individua i punti al di sopra del piano.
La seconda individua i punti al di sotto del piano.
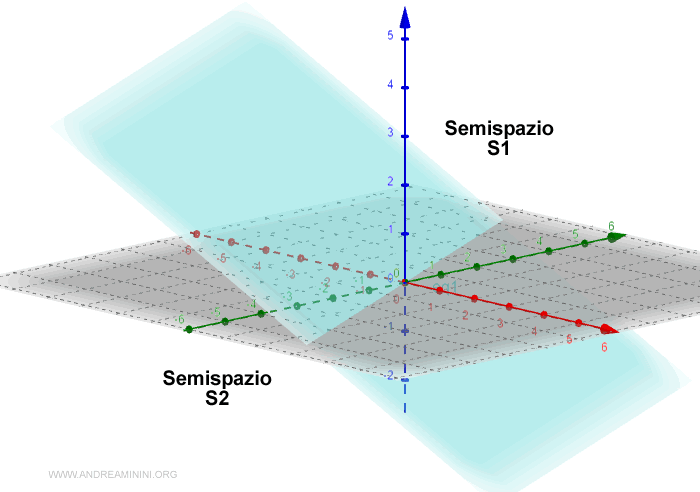
L'unione dei due semispazi corrisponde all'insieme Rn.
$$ S_1 + S_2 = R^n $$
L'intersezione di un numero finito di semispazi determina un poliedro.
Un esempio di iperpiano
Ho un vettore di coefficienti anche detto gradiente dell'iperpiano.
$$ a = \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$
un vettore di variabili
$$ x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} $$
e uno scalare b
$$ b = 0 $$
L'iperpiano è il seguente
$$ a^Tx = b $$
$$ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}^T \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = 0 $$
$$ \begin{pmatrix} 2 , 1 , 3 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = 0 $$
$$ 2x_1+x_2+3x_3 = 0 $$
Considerando x1,x2,x3 come coordinate x,y,z dello spazio, l'equazione dell'iperpiano corrisponde a un piano dello spazio R3.

E così via.
