Come calcolare l'angolo tra retta e piano nello spazio
Per calcolare l'angolo tra una retta e un piano, si calcola il prodotto scalare dei vettori direttori della retta e della sua proiezione sul piano, in rapporto al prodotto delle norme dei vettori direttori.
Esempio
Ho l'equazione cartesiana di un piano α nello spazio
$$ x-2y+3z=0 $$
e l'equazione vettoriale una retta
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} + t \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} $$
Ecco la rappresentazione grafica della retta e del piano
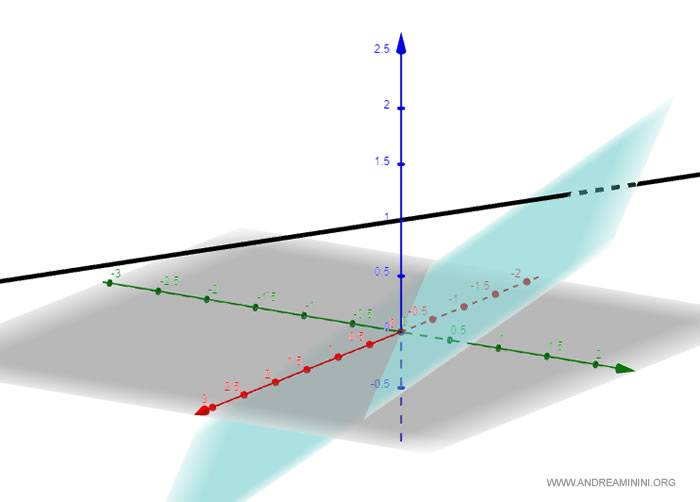
Per calcolare l'angolo tra la retta e il piano, devo trovare la proiezione della retta sul piano.
Devo trovare nel fascio di piani della retta quello perpendicolare al piano.
Trasformo l'equazione della retta da vettoriale a cartesiana.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} + t \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} $$
Prima la trasformo in parametrica
$$ \begin{cases} x = 2 -2t \\ y = -1 + t \\ z = 1 \end{cases} $$
Poi scelgo un'equazione del sistema per definire il parametro t.
Scelgo la seconda.
$$ \begin{cases} x = 2 -2t \\ y = -1 + t \\ z = 1 \end{cases} $$
$$ \begin{cases} x = 2 -2t \\ t=y +1 \\ z = 1 \end{cases} $$
$$ \begin{cases} x = 2 -2(y+1) \\ z = 1 \end{cases} $$
$$ \begin{cases} x = -2y \\ z = 1 \end{cases} $$
$$ \begin{cases} x +2y = 0 \\ z -1 = 0 \end{cases} $$
Ho così trovato l'equazione cartesiana della retta nello spazio.
E' un sistema che determina l'intersezione di due piani dello spazio.
A questo punto calcolo il fascio di piani.
$$ ( x +2y ) + k ( z-1 ) = 0 $$
$$ x +2y + kz -k = 0 $$
Il vettore normale del fascio di piani è
$$ n_f = \begin{pmatrix} 1 \\ 2 \\ k \end{pmatrix} $$
Il piano α è
$$ x-2y+3z=0 $$
Quindi il vettore normale del piano α è
$$ n = \begin{pmatrix} 1 \\ -2 \\ 3 \end{pmatrix} $$
Devo trovare un valore di k che renda il prodotto scalare dei due vettori normali uguale a zero.
I tale circostanza i due vettori sono ortogonali ossia perpendicolari.
$$ < n_f , n > = 0 $$
$$ 1 \cdot 1 + 2 \cdot (-2) + k \cdot 3 = 0 $$
$$ -3 + 3k = 0 $$
$$ k = \frac{3}{3} = 1 $$
Con k=1 i due vettori sono ortogonali.
Quindi sostituisco k=1 nell'equazione del fascio dei piani.
$$ x +2y + kz -k = 0 $$
$$ x +2y + z -1 = 0 $$
Ho trovato il piano che contiene la retta ed è perpendicolare al piano α.
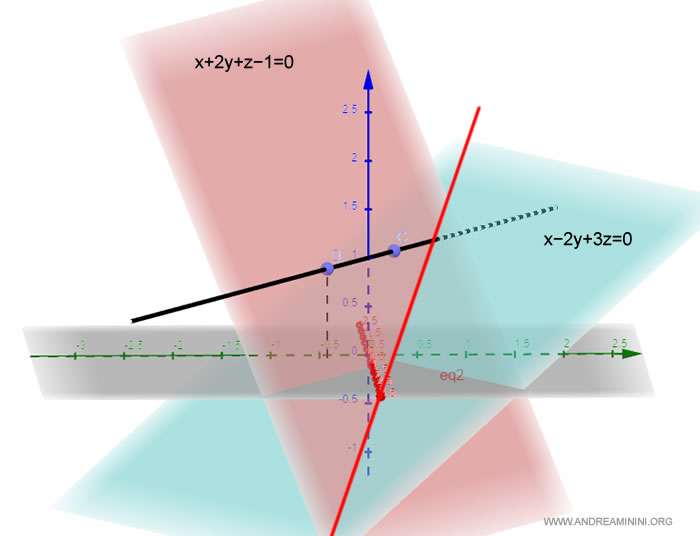
Questo mi permette di trovare la proiezione della retta sul piano α ( retta di colore rosso ).
La proiezione della retta è semplicemente l'insieme dei punti di intersezione tra i due piani:
Quindi, posso scriverla come sistema di equazioni dei due piani:
$$ \begin{cases} x +2y + z -1 = 0 \\ x-2y+3z=0 \end{cases} $$
Ora conosco sia l'equazione della retta e sia della sua proiezione sul piano α.
$$ r: \begin{cases} x +2y = 0 \\ z -1 = 0 \end{cases} $$
Posso calcolare l'angolo delle due rette tramite i loro vettori direttori ( o vettori normali ).
$$ cos(α) = \frac{<v_1,v_2>}{||v_1|| \cdot ||v_2||} $$
In questo modo trovo anche l'angolo della retta con il piano α.
Trasformo l'equazione della retta proiettata in equazione parametrica:
$$ \begin{cases} x +2y + z -1 = 0 \\ x-2y+3z=0 \end{cases} $$
$$ \begin{cases} x +2y + t -1 = 0 \\ x-2y+3t=0 \\ z=t \end{cases} $$
$$ \begin{cases} x = -2y - t +1 \\ (-2y - t +1)-2y+3t=0 \\ z=t \end{cases} $$
$$ \begin{cases} x = -2y - t +1 \\ -4y+2t +1=0 \\ z=t \end{cases} $$
$$ \begin{cases} x = -2y - t +1 \\ y=\frac{+2t +1}{4} \\ z=t \end{cases} $$
$$ \begin{cases} x = -2(\frac{+2t +1}{4} ) - t +1 \\ y=\frac{+2t +1}{4} \\ z=t \end{cases} $$
$$ \begin{cases} x = \frac{-2t -1}{2} - t +1 \\ y=\frac{+2t +1}{4} \\ z=t \end{cases} $$
$$ \begin{cases} x = \frac{-4t +1}{2} \\ y=\frac{+2t +1}{4} \\ z=t \end{cases} $$
$$ \begin{cases} x = -2t + \frac{1}{2} \\ y=\frac{t }{2} +\frac{1}{4} \\ z=t \end{cases} $$
Quindi il vettore direttore della retta proiettata è
$$ v_p = \begin{pmatrix} -2 \\ \frac{1}{2} \\ 1 \end{pmatrix} $$
Il vettore direttore della retta r già lo conosco
$$ v_r = \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} $$
Posso finalmente calcolare l'angolo tra le due rette:
$$ cos(α) = \frac{<v_p,v_r>}{||v_p|| \cdot ||v_r||} $$
$$ cos(α) = \frac{(-2)(-2)+\frac{1}{2} \cdot 1 + 1 \cdot 0}{ \sqrt{-2^2+( \frac{1}{2})^2 + 1^2} \cdot \sqrt{(-2)^2+1^2+0^2} } $$
$$ cos(α) = \frac{\frac{9}{2} }{ \sqrt{ \frac{21}{4} } \cdot \sqrt{5} } = 0.8783 $$
Ora per calcolare l'ampiezza dell'angolo devo soltanto calcolare l'arcocoseno
$$ α = arccos(cos(α)) $$
$$ α = arccos( 0.8783) = 0.49 π $$
Un angolo misura 0.49 radianti (π) circa 28°.
Quindi l'altro angolo supplementare misura 2.65 radianti (π). Circa 152°
$$ π - α = π - 0.49 = 2.65 π $$
Anche Geogebra conferma i calcoli.
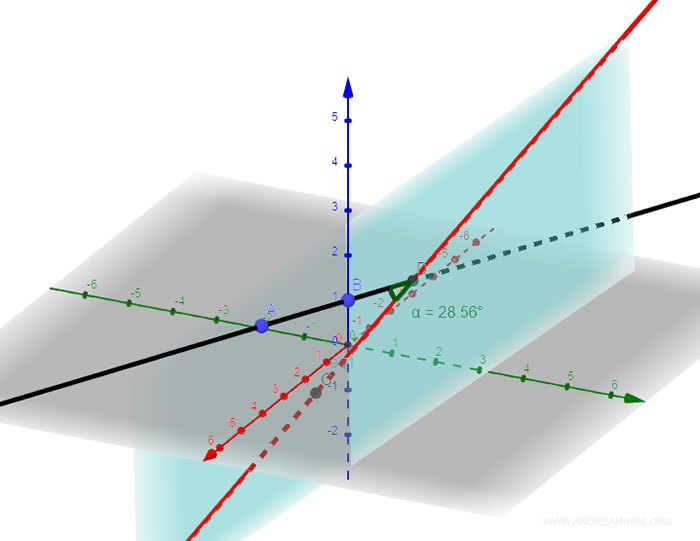
E così via.
