Come calcolare l'angolo delle rette sghembe nello spazio
Due rette sghembe qualsiasi nello spazio a tre dimensioni (x,y,z) formano un angolo di ampiezza α.
Per trovare l'ampiezza dell'angolo, devo calcolare il coseno dell'ampiezza di α, sapendo che il coseno di α è uguale al rapporto tra il prodotto scalare dei vettori direttori delle rette <v1,v2> e il prodotto tra le norme dei due vettori direttori ||v1||*||v2||. $$ cos(α) = \frac{<v_1,v_2>}{||v_1|| \cdot ||v_2||} $$
Il procedimento è identico al calcolo degli angoli delle rette complanari o nel piano a due dimensioni.
Un esempio pratico
Ho due rette nello spazio
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$
Sono due rette sghembe perché si trovano su due piani distinti dello spazio e non incidenti.
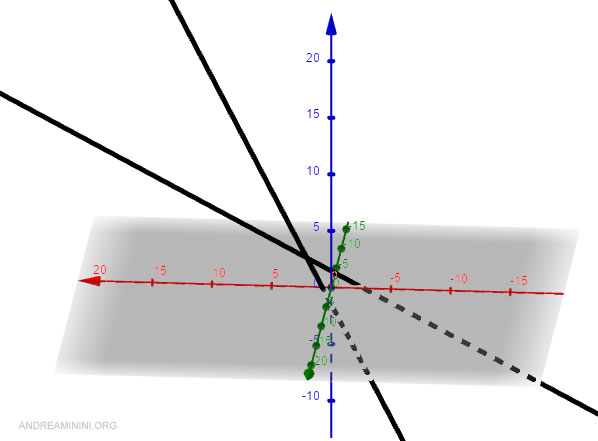
Nota. Per calcolare l'angolo di due rette qualsiasi nello spazio non occorre che siano complanari o incidenti.
I vettori direttori delle rette sono:
$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$
Quindi calcolo il coseno di alfa.
$$ cos(α) = \frac{<v_1,v_2>}{||v_1|| \cdot ||v_2||} $$
$$ cos(α) = \frac{ 1 \cdot 3 + 2 \cdot 1 + 3 \cdot2 }{ \sqrt{1^2+2^2+3^2} \cdot \sqrt{3^2+1^2+2^2} } $$
$$ cos(α) = \frac{ 11 }{ \sqrt{14} \cdot \sqrt{14} } $$
$$ cos(α) = \frac{ 11 }{ 14 } = 0.7857 $$
E' il valore del coseno dell'angolo.
Attenzione. Non è ancora l'ampiezza dell'angolo α. Si tratta soltanto del valore del coseno nell'angolo α.
Per conoscere l'ampiezza dell'angolo devo calcolare l'arcocoseno di 0.7857.
$$ \arccos(0.7857) = 0.666969438 π $$
L'ampiezza dell'angolo è 0.666969438 π ossia 38,21°.
Quindi, se le due rette fossero complanari formerebbero due coppie di angoli pari a
$$ α = 38,21° \\ 180° - α = 141,79° $$
o in radianti
$$ α = 0.666969438 π \\ π - α = 2,4746 π $$
E così via.
