Il coseno iperbolico
Il coseno iperbolico (cosh) è una funzione matematica iperbolica definita come la metà della somma della funzione esponenziale di x e l'inverso della funzione esponenziale di x. E' indicata con il simbolo cosh o ch. $$ \cosh(x) = \frac{e^x + e^{-x}}{2} $$ Dove "e" è il simbolo di Nepero (e=2,71...) ossia la base dei logaritmi naturali.
Ecco le principali caratteristiche del coseno iperbolico.
- Il suo dominio corrisponde con l'insieme dei numeri reali (R).
- E' una funzione continua
- E' una funzione monotòna
- E' una funzione pari in ogni punto $$ \cosh(x) = \cosh(-x) $$
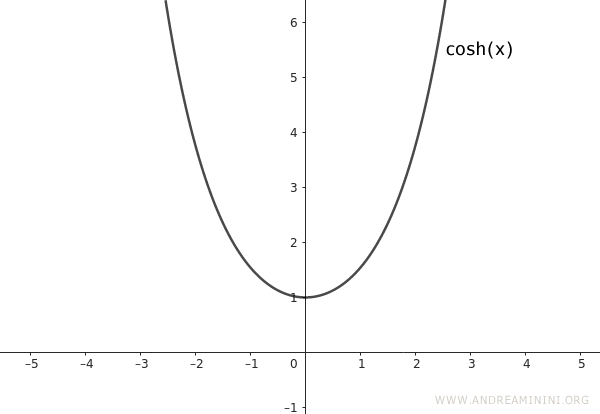
- E' una funzione simmetrica rispetto all'asse y. La sua curva ha la stessa forma di una parabola con un asse di simmetria verticale sull'asse y.
- Per x=0 il coseno iperbolico vale 1 ossia cosh(0)=1
- E' decrescente nell'intervallo (-∞, 0) e crescente nell'intervallo (0,∞)
- La derivata del coseno iperbolico è il seno iperbolico. $$ D [ \cosh(x) ] = \sinh(x) $$
- E' una funzione invertibile. La funzione inversa è l'arcocoseno iperbolico.
Il grafico della funzione
E così via.
