Arcocoseno iperbolico

L'arcocoseno iperbolico (acosh o cosh^-1) è la funzione inversa del coseno iperbolico. In altre parole se $$ y = \text{acosh}(x) $$ allora $$ x = \text{cosh(y)} $$

Le principali caratteristiche della tangente iperbolica sono le seguenti

• Dominio. La funzione acosh(x) è definita per valori di x compresi tra 1 e +∞. $$ D_f = [1, +∞) $$
• Codominio. Il codominio della funzione corrisponde all'intervallo [0,∞). $$ C_f = [0, ∞) $$
• Caratteristiche. E' una funzione continua, monotòna e crescente
• Intercette. Per x=1 vale y=0 ossia acosh(1)=0
• Derivata. La derivata dell'arcocoseno iperbolico è $$ D[ \text{acosh}(x) ] = \frac{1}{ \sqrt{x^2-1} } $$
• Limiti. La funzione tende a +∞ quando x tende a più infinito. $$ \lim_{x \rightarrow \infty} \text{acosh}(x) = ∞ $$
• Funzione inversa. E' una funzione invertibile. La funzione inversa è il coseno iperbolico.

Il grafico della funzione

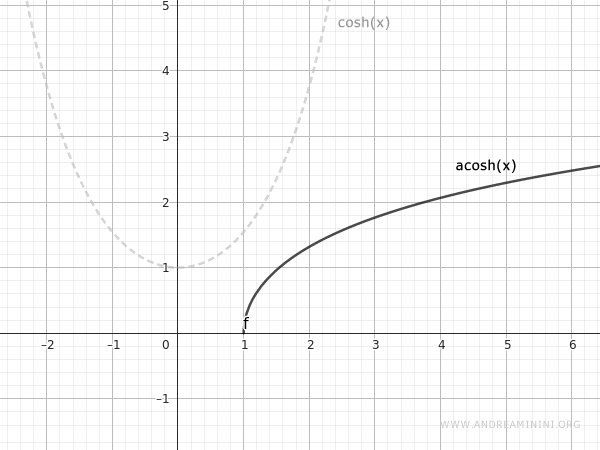
E così via.