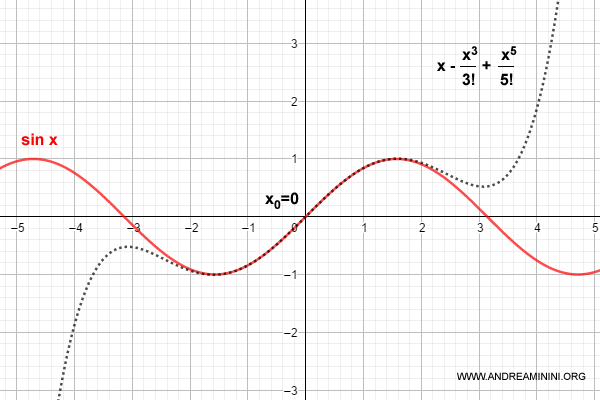
Come approssimare la funzione seno con il polinomio di Taylor o Mac Laurin
In questo esercizio devo approssimare la funzione trigonometrica del seno con un polinomio di Taylor.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$
Scelgo come centro x0=0 per ricondurmi alla formula di Mac Laurin e come grado del polinomio n=5.
Nota. La formula di Mac Laurin calcola il polinomio di Tayler nel caso specifico in cui x0=0. I calcoli della formula di MacLaurin sono molto più rapidi. Quindi, se è possibile scegliere un punto x0 qualsiasi è sempre meglio scegliere x0=0 e ricondursi a MacLaurin.
Per calcolare il polinomio svolgo i calcoli per ogni termine della serie Taylor in modo separato, dal primo (n=0) all'ultimo (n=5).
Poi aggiungo alla fine il resto di Peano.
Il grado n=0
$$ \frac{D^{0} \sin 0 }{0!} \cdot (x-0)^0 $$
$$ \frac{\sin 0 }{1} \cdot 1 $$
$$ = 0 $$
Il primo termine della serie è nullo.
Il grado n=1
$$ \frac{D^{1} \sin 0 }{1!} \cdot (x-0)^1 $$
$$ \frac{\cos 0 }{1} \cdot (x) $$
$$ = x $$
Il secondo termine della serie è x.
Il grado n=2
$$ \frac{D^{2} \sin 0 }{2!} \cdot (x-0)^2 $$
$$ \frac{- \sin 0 }{2!} \cdot x^2 $$
$$ = 0 $$
Il terzo termine della serie è 0.
Il grado n=3
$$ \frac{D^{3} \sin 0 }{3!} \cdot (x-0)^3 $$
$$ \frac{- \cos 0 }{3!} \cdot x^3 $$
$$ = \frac{-1}{3!} x^3 $$
Il quarto termine della serie è -x3/3!
Nota. Piuttosto di calcolare la derivata terza, quarta, ecc. della funzione seno a ogni passaggio dello sviluppo di Taylor o MacLaurin è più facile e immediato calcolare la derivata prima della precedente derivata. Ad esempio, in n=2 la funzione è -sin(0). Quindi, in n=3 la derivata prima della precedente è D(-sin(0)] = - cos(0). Ho così ottenuto rapidamente la derivata terza del seno.
Il grado n=4
$$ \frac{D^{4} \sin 0 }{4!} \cdot (x-0)^4 $$
$$ \frac{\sin 0 }{4!} \cdot x^4 $$
$$ = 0 $$
Il quinto termine della serie è zero.
Il grado n=5
$$ \frac{D^{5} \sin 0 }{5!} \cdot (x-0)^5 $$
$$ \frac{\cos 0 }{5!} \cdot x^5 $$
$$ = \frac{1}{5!} x^5 $$
Il sesto termine della serie è x5/4!.
Ho calcolato tutti i termini del polinomio di Taylor di grado n=5.
Mi manca da calcolare soltanto il resto del polinomio.
Il resto di Peano
Per calcolare il resto di Peano utilizzo la notazione "o piccolo".
$$ R_n = o((x-x_0)^n) $$
Dove x0=0 e n=5
$$ R_5 = o((x-0)^5) $$
$$ R_5 = o(x^5) $$
Nota. La notazione "o piccolo" vuol dire che il resto di Peano Rn è un infinitesimo di ordine superiore rispetto a x5, ossia tende a zero più velocemente di x^5 per x->x0. $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$
A questo punto scrivo il polinomio di Taylor sommando tutti i termini appena trovati
$$ p_5 = 0 + x + 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} + o(x^5) $$
$$ p_5 = x - \frac{x^3}{3!} + \frac{x^5}{5!} + o(x^5) $$
Ho calcolato il polinomio di Taylor.
Nota. In questo caso, essendo x0=0, si tratta di un polinomio di Mac Laurin. Il calcolo è comunque lo stesso per qualsiasi x0≠0.
Il polinomio di grado n=5 approssima abbastanza bene la funzione seno nell'intorno di x0=0.
Come generalizzare il polinomio per un n qualsiasi
Volendo posso anche generalizzare il polinomio per un n qualsiasi.
Guardando la serie completa, quella con i valori nulli, balzano subito all'occhio due schemi regolari
$$ 0 + x + 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} + ... $$
- La serie è composta solo dai termini con indice dispari (n=1, n=3, n=5) mentre quelli pari sono nulli.
Nota. Il primo termine è n=0 mentre n=1 è il secondo.
- I termini dispari si alternano di segno.
Un numero dispari lo ottengo moltiplicando per due l'indice e aggiungendo 1 ossia (2n+1).
In questo modo la serie considera solo i termini dispari della serie.
$$ x - \frac{x^3}{3!} + \frac{x^5}{5!} + ... $$
A questo punto è semplice definire l'alternanza del segno, basta moltiplicare ogni termine della precedente serie per -1n che assume i valori unitari alternati da 0 in poi.
Quindi, la serie di Taylor/Mac Laurin del seno generalizzata potrebbe essere
$$ p_n = x - \frac{x^3}{3!} + \frac{x^5}{5!} + ... + (-1)^n \cdot \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+1}) $$
C'è però ancora un'irregolarità da correggere nell'o piccolo.
Nella serie completa il polinomio P2n+1 è uguale al successivo P2n+2 di indice pari, perché i termini pari sono sempre nulli e la serie non varia.
$$ P_{2n+1} = P_{2n+2} $$
Quindi posso scrivere nel polinomio di Taylor direttamente o(x2n+2).
Pertanto, la serie di Taylor/Mac Laurin del seno generalizzata è la seguente
$$ p_n = x - \frac{x^3}{3!} + \frac{x^5}{5!} + ... + (-1)^n \cdot \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+2}) $$
Adesso la serie di Talor del seno per un n qualsiasi è completa.
E così via.