Esercizio studio della funzione 6

Devo studiare il grafico di questa funzione

$$ x^3 -3x +2 $$

Per farlo utilizzo gli strumenti dell'analisi matematica

Dominio

Il dominio della funzione è l'insieme dei numeri reali

$$ D_f = R $$

La funzione f(x) è definita in ogni punto della'sse reale

Intercette

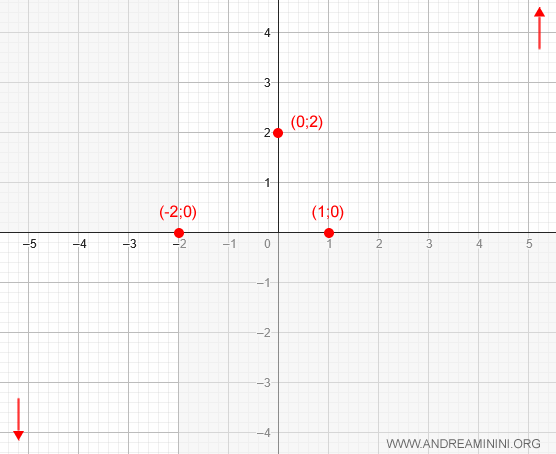
Calcolo l'intersezione della funzione con l'asse delle ordinate ponendo x=0

$$ y = 0^3 -3 \cdot 0 +2 = 2 $$

La funzione passa per il punto (0;2) alle coordinate x=0 e y=2

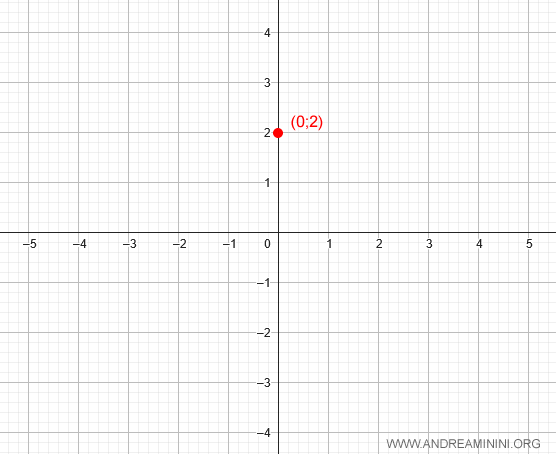
Per calcolare l'intersezione con l'asse delle ascisse devo risolvere l'equazione

$$ x^3 -3x +2 = 0 $$

A occhio mi accorgo che l'equazione si annulla per x=1. Ne approfitto per ridurre il grado dell'equazione usando il metodo di Ruffini.

$$ \begin{array}{c|lcc|r} & 1 & 0 & -3 & 2 \\ 1 & & 1 & 1 & -2 \\ \hline & 1 & 1 & -2 & 0 \end{array} $$

Quindi, l'equazione equivalente è

$$ (x-1) \cdot (x^2+x-2) $$

Il primo fattore (x-1) si annulla per x=1

Il secondo fattore è un'equazione di 2° grado che si annulla per x=-2 e x=1/2

$$ x= \frac{-1 \pm \sqrt{1-4(1)(-2)}}{2} $$

$$ x= \frac{-1 \pm \sqrt{9}}{2} $$

$$ x= \frac{-1 \pm 3}{2} $$

$$ x = \begin{cases} \frac{-1-3}{2}=-2 \\ \\ \frac{-1+3}{2} = \frac{2}{2} = 1 \end{cases} $$

Pertanto, la funzione f(x) interseca l'asse x nei punti x₁=-2, x₂=1

Quindi, il grafico della funzione passa per i punti (-2;0) e (1;0)

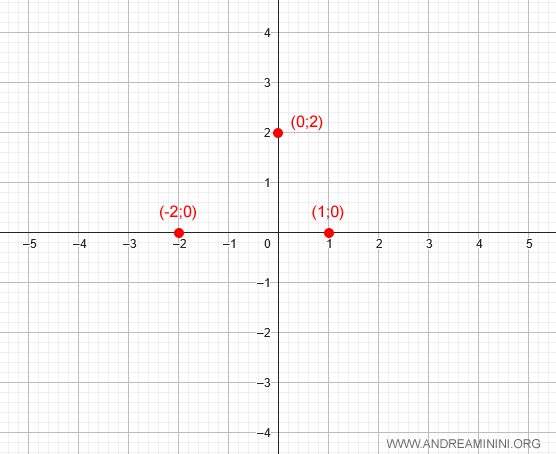
Asintoti

La funzione non ha punti in cui non è definita. Quindi non ci sono asintoti verticali.

Per trovare gli asintoti orizzontali calcolo il limite della funzione per x tendente a più infinito e a meno infinito.

$$ \lim_{x \rightarrow +\infty} x^3 - 3x +2 = + \infty $$

$$ \lim_{x \rightarrow -\infty} x^3 - 3x +2 = - \infty $$

Non ci sono asintoti orizzontali.

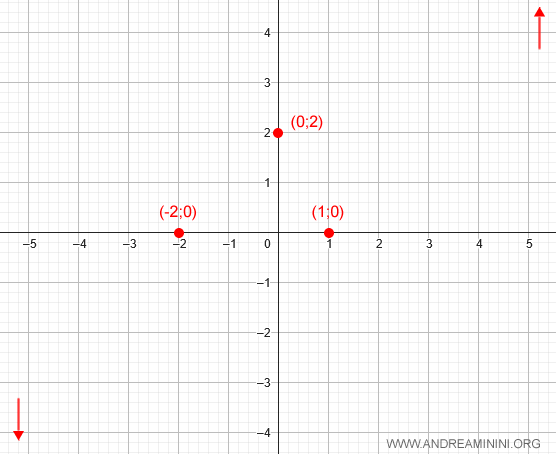
La funzione f(x) tende a +∞ per x che tende a infinito e a -∞ per x che tende a meno infinito.

Aggiungo il comportamento asintotico della funzione nel grafico come promemoria.

Studio del segno

Per studiare il segno della funzione y=x³-3x+2 riprendo l'espressione equivalente che ho calcolato con il metodo di Ruffini.

$$ (x-1) \cdot (x^2+x-2) $$

In questo modo è più facile studiare il segno.

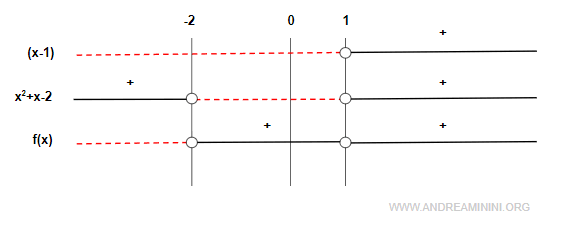
Il fattore (x-1) è positivo per x>1 mentre il fattore x2+x-2 è una parabola rivolta verso l'alto di cui già conosco le radici in x₁=-2 e x₂=1.

Pertanto, la funzione f(x)=x³-3x+2 è negativa nell'intervallo (-∞,-2) e positiva nell'intervallo (-2,+∞)

Elimino dal diagramma cartesiano le aree in cui la funzione non passa.

La crescenza e decrescenza

Per studiare la crescenza e la decrescenza della funzione calcolo la sua derivata prima

$$ f'(x) = D_x[ x^3 -3x +2 ] = 3x^2 -3 $$

Poi ne studio il segno

$$ 3x^2 - 3 > 0 $$

$$ 3x^2 > 3 $$

$$ x^2 > \frac{3}{3} $$

$$ x^2 > 1 $$

La derivata prima è positiva negli intervalli (-∞,-1) e (1,∞) e si annulla nei punti x=-1 e x=1

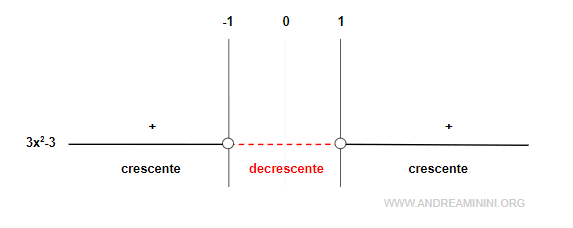
Lo studio del segno della derivata prima mi fornisce molte informazioni utili

• La funzione f(x) è crescente nell'intervallo (-∞,-1)
• Nel punto x=-1 c'è un massimo locale perché la derivata è nulla f'(x)=0 e la funzione è crescente a sinistra e decrescente a destra. Quindi, il punto (-1;4) è un massimo locale.

  Nota. Per ottenere le coordinate (x;y) del punto sostituisco x=-1 nella funzione f(x) e ottengo $$ y=x^3-3x+2 = (-1)^3-3 \cdot (-1) + 2 = -1+3+2 = 4 $$ In questo modo ottengo entrambe le coordinate del punto ossia x=-1 e y=4

• La funzione f(x) è decrescente nell'intervallo (-1,1)
• Nel punto x=1 c'è un minimo locale perché la derivata è nulla f'(x)=0 e la funzione è decrescente a sinistra e crescente a destra. Quindi, il punto (1;0) è un minimo locale.

  Nota. Per ottenere le coordinate (x;y) del punto sostituisco x=1 nella funzione f(x) e ottengo $$ y=x^3-3x+2 = (1)^3-3 \cdot (1) + 2 = 1-3+2 = 0 $$ In questo modo ottengo entrambe le coordinate del punto ossia x=1 e y=0

• La funzione f(x) è crescente nell'intervallo (1,∞)

Aggiungo tutte queste informazioni al grafico della funzione

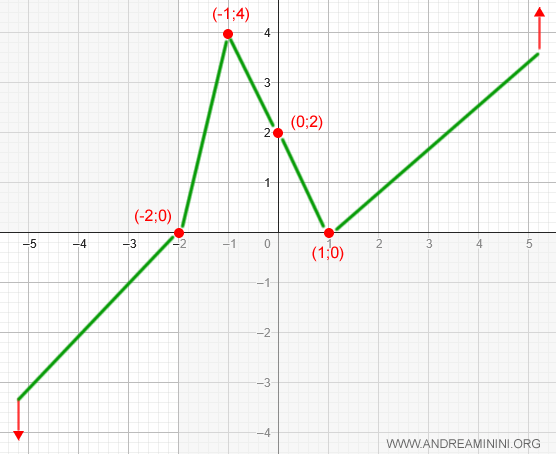
La convessità e concavità

Per studiare i tratti in cui la funzione è convessa o concava calcolo la derivata seconda della funzione

$$ f''(x) = D_x[ 3x^2 -3 ] = 6x $$

Poi studio il segno della derivata seconda

La derivata seconda è negativa nell'intervallo (-∞,0) e positiva nell'intervallo (0,∞).

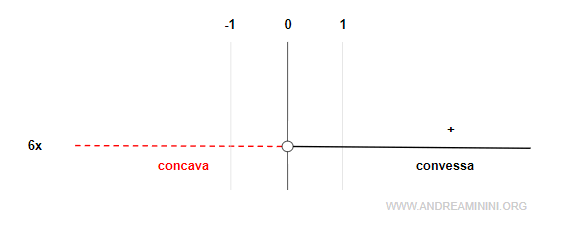
Quindi, la funzione è concava nell'intervallo (-∞,0) e convessa nell'intervallo (0,∞).

Quest'ultima informazione mi permette di completare il grafico della funzione

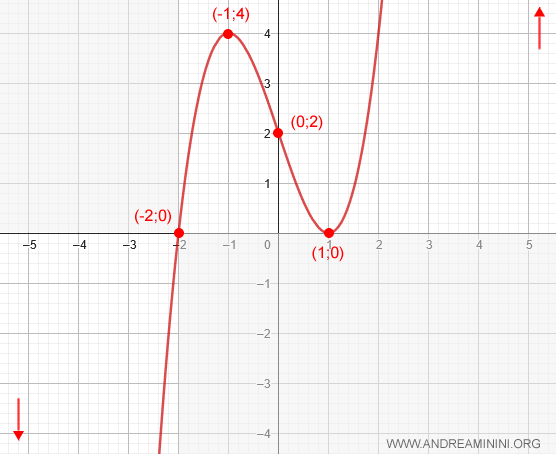
E così via.