Esercizio serie 4

Studiare il carattere della serie

$$ \frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{9}+... $$

Posso riscrivere la serie con una formula

$$ \sum_{n=1}^{\infty} \frac{1}{2n} $$

Si tratta di una serie a termini non negativi. Quindi non può essere indeterminata.

Verifico se soddisfa la condizione necessaria di convergenza delle serie.

$$ \lim_{n \rightarrow \infty} \frac{1}{2n} = 0 $$

La serie soddisfa la condizione necessaria di convergenza. Quindi, può essere convergente o divergente.

Studio la serie usando il criterio degli infinitesimi delle serie a termini non negativi.

Per p>1 il limite è infinito. Quindi non posso affermare che sia convergente.

$$ \lim_{n \rightarrow \infty} n^p \cdot \frac{1}{2n} = \infty $$

Per p=1, invece, il limite è diverso da zero.

$$ \lim_{n \rightarrow \infty} n^p \cdot \frac{1}{2n} = \frac{1}{2} $$

Quindi, secondo il criterio degli infinitesimi la serie è divergente.

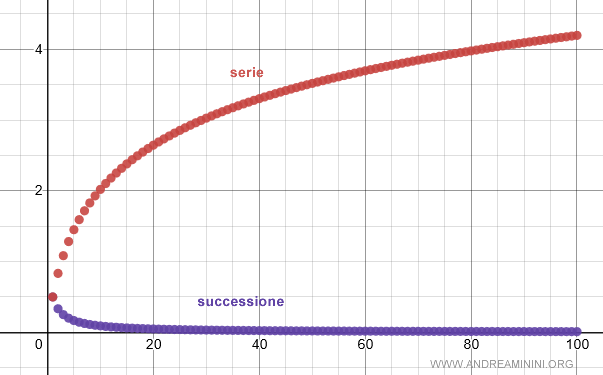
E così via.