Esercizio serie 1
Devo verificare il carattere della serie
$$ \sum_{n=1}^{\infty} \frac{n}{n+1} $$
Si tratta di una serie a termini non negativi, quindi può essere una serie indeterminata.
Verifico se la serie soddisfa la condizione necessaria di convergenza delle serie
$$ \lim_{n \rightarrow \infty} \frac{n}{n+1} = \frac{ \infty }{ \infty } $$
Il limite è una forma indeterminata del tipo ∞/∞.
Applico il teorema di de L'Hopital e calcolo il limite del rapporto tra la derivata del numeratore e la derivata del denominatore.
$$ \lim_{n \rightarrow \infty} \frac{D[n]}{D[n+1]} = \lim_{n \rightarrow \infty} \frac{1}{1} = 1 $$
Il limite del termine generale della serie per n→∞ non è uguale a zero. Quindi, la serie non soddisfa la condizione necessaria di convergenza.
Non essendo indeterminata, né convergente, deduco per esclusione che la serie è divergente.
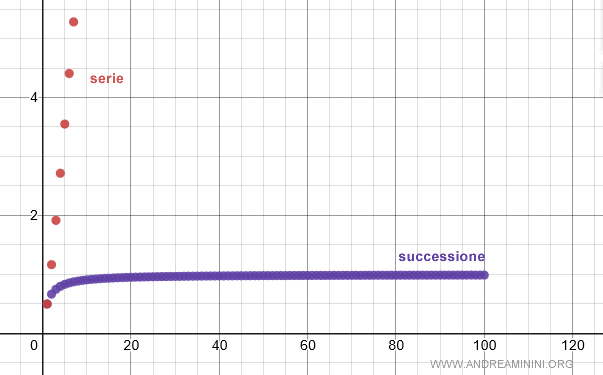
Soluzione
La serie è divergente
E così via.
