Le equazioni cartesiane e parametriche

Un sottospazio W dello spazio vettoriale Rⁿ nel campo dei numeri reali K=R può essere rappresentato ed espresso con equazioni cartesiane oppure con equazioni parametriche:

Qual è la differenza tra equazioni cartesiane e parametriche?

• Le equazioni cartesiane sono equazioni lineari omogenee e linearmente indipendenti delle componenti elementi di un vettore. Sono utili per verificare se il vettore v appartiene o meno al sottospazio Rⁿ.
  

  Esempio
  $$W = \{ (x,y) \in R^2 , x-y =0 \}$$

• Le equazioni parametriche sono equazioni che usano i parametri linearmente indipendenti. Sono utili per descrivere tutti degli elementi di un sottospazio.
  

  Esempio
  $$\begin{cases} x=t \\ y=t \end{cases}$$

Le caratteristiche delle equazioni parametriche e cartesiane

Le equazioni cartesiane e parametriche hanno alcune caratteristiche generali:

• In un sottospazio W esistono infinite equazioni cartesiane e infinite equazioni parametriche alternative ed equivalenti tra loro.

  Esempio $$x-y =0 \Longleftrightarrow k·x-k·y =0$$ $$\begin{cases} x=t \\ y=t \end{cases} \Longleftrightarrow \begin{cases} k·x=t \\ k·y=t \end{cases}$$

• Un'equazione parametrica equivale a una base vettoriale, e viceversa.

  Esempio $$\begin{cases} x=t \\ y=t \end{cases} \Longleftrightarrow v(x,y) = t·B$$

• Il numero minimo di equazioni cartesiane necessarie per descrivere il sottospazio W è uguale alla codimensione del sottospazio W nello spazio vettoriale V.
  
  $$codim_k(W) = dim_k(V) - dim_k(W)$$
• Il numero minimo di parametri (t) necessari per descrivere il sottospazio W è uguale alla dimensione del sottospazio W nello spazio vettoriale V, ossia al numero di elementi della base vettoriale B di W.
  
  $$dim_k(W)$$

Come trasformare un'equazione cartesiana in equazione parametrica

Dato un sottospazio W nello spazio vettoriale V=R² nel campo K=W

$$W ⊂ V$$

Ad esempio, prendo come esempio il sottospazio W individuato dall'equazione cartesiana x-y=0.

$$W = \{ (x,y) \in R^2 \:\:,\:\: x-y=0 \}$$

Il sottospazio W è composto da tutti i punti della retta x-y=0.

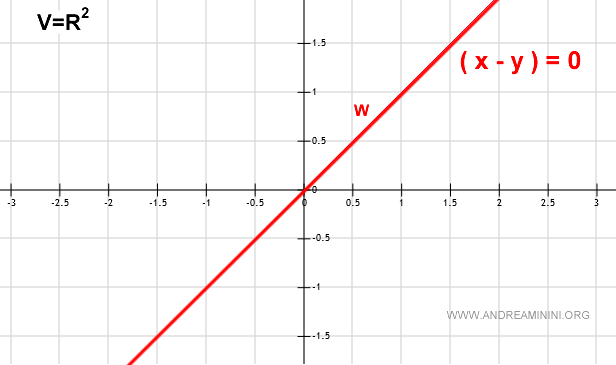
Per trasformare l'equazione cartesiana in un'equazione parametrica, aggiungo un parametro t e lo associo a un'espressione a mia scelta.

Ad esempio, al sistema aggiungo il parametro t=y.

$$\begin{cases} x-y=0 \\ t=y \end{cases}$$

Nota. La scelta del parametro è del tutto arbitraria. In questo caso ho scelto t=y perché è quella che semplifica di più i calcoli ma avrei potuto optare per molte altre scelte parametriche.

quindi

$$\begin{cases} x-(t)=0 \\ t=y \end{cases}$$

$$\begin{cases} x=t \\ y=t \end{cases}$$

Ho così ottenuto le equazioni parametriche del sistema.

Al variare del parametro t, con le equazioni parametriche posso ottenere tutti i vettori del sottospazio W.

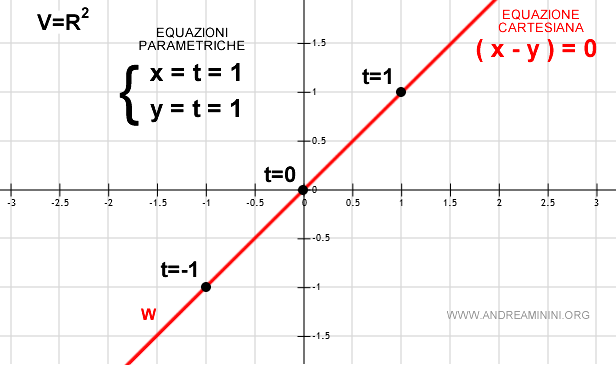
In questo caso è molto semplice, si tratta di un solo vettore v con due coordinate cartesiane (x,y) e un solo parametro t.

$$v ( x,y) = \begin{cases} x=t \\ y=t \end{cases}$$

A questo punto posso scrivere il sistema di equazioni parametriche sotto forma vettoriale.

$$\begin{cases} x=t \\ y=t \end{cases} \Rightarrow \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} t \\ t \end{pmatrix}$$

ossia

$$\begin{pmatrix} x \\ y \end{pmatrix} = t \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$

Ho così trovato il vettore w=(1,1) che identifica la base del sottospazio.

Per trovare qualsiasi punto mi basta moltiplicare il vettore w per il parametro t.

E' molto importante ricordarsi che scegliere un'equazione parametrica equivale a scegliere una base del sottospazio W.

Nota. Se avessi scelto una parametrizzazione diversa da t=y, adesso avrei un'altra base ossia un altro vettore diverso da w=(1,1).

Come convertire un'equazione parametrica in equazione cartesiana

Per trovare l'equazione cartesiana di un'equazione parametrica, svolgo il percorso inverso.

$$v ( x,y) = \begin{cases} x=t \\ y=t \end{cases}$$

Nel sistema di equazioni parametriche metto in evidenza una delle due coordinate cartesiane (x,y).

Ad esempio, scelgo t=x.

$$v ( x,y) = \begin{cases} t=x \\ y=t \end{cases}$$

Poi la sostituisco al parametro t nell'altra equazione.

$$v ( x,y) = \begin{cases} t=x \\ y=(x) \end{cases}$$

$$v ( x,y) = \begin{cases} t=x \\ t=y \end{cases}$$

Essendo entrambe le equazioni del sistema uguali al parametro t, posso anche scriverle nella seguente forma:

$$x = y$$

quindi

$$x - y = 0$$

Ho così trovato l'equazione cartesiana del sottospazio W.