Le parabole degeneri
Una parabola del fascio è detta "parabola degenere" quando per un determinato valore del parametro λ si trasforma in una retta
Nel fascio di parabole un determinato valore del parametro λ elimina la variabile y o il termine quadratico x2 dall'equazione.
In questi casi la parabola "degenera" in una retta o in una coppia di rette.
Un esempio pratico
Considero il fascio di parabole
$$ (y-x^2+3x-2) + \lambda \cdot (y+x^2-5x+4) = 0 $$
Questa equazione genera infinite parabole con l'apertura verso l'alto o verso il basso a seconda del valore del parametro $ \lambda $
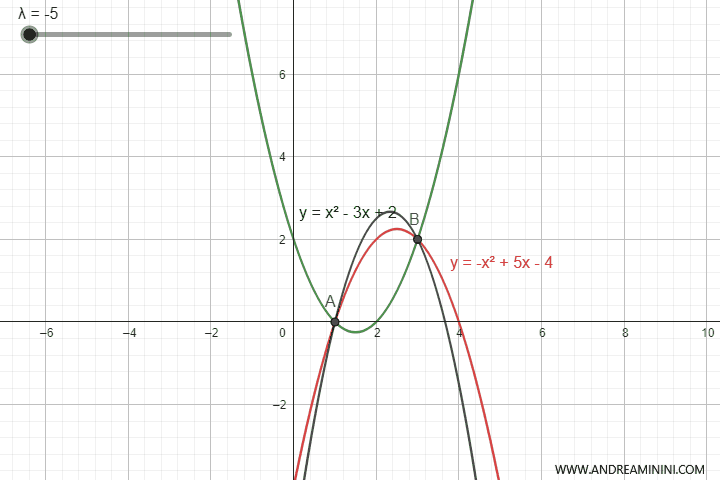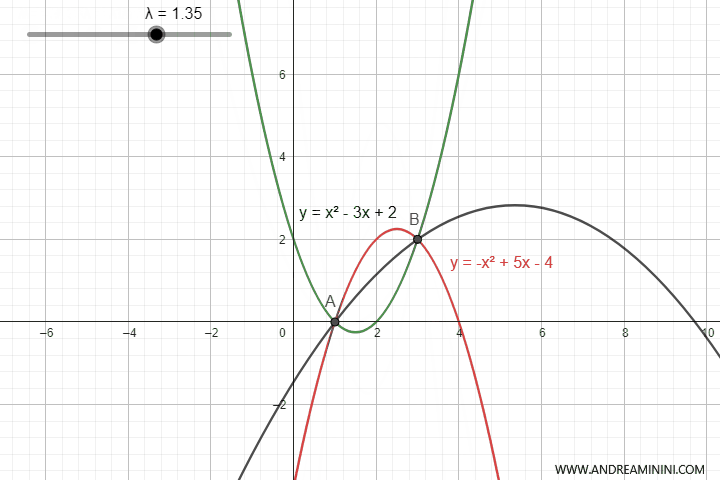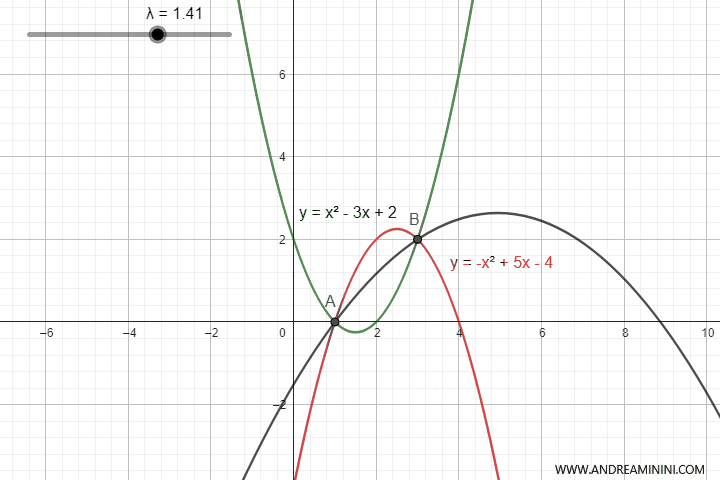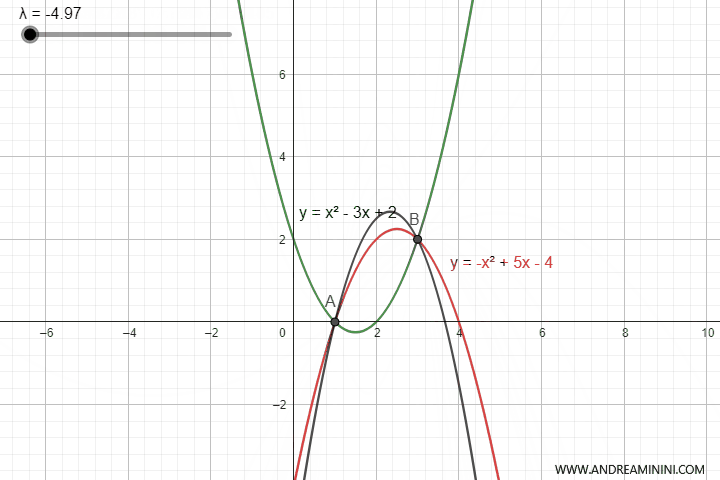
Tuttavia, in alcuni valori di $ \lambda $ la parabola degenera in una retta.
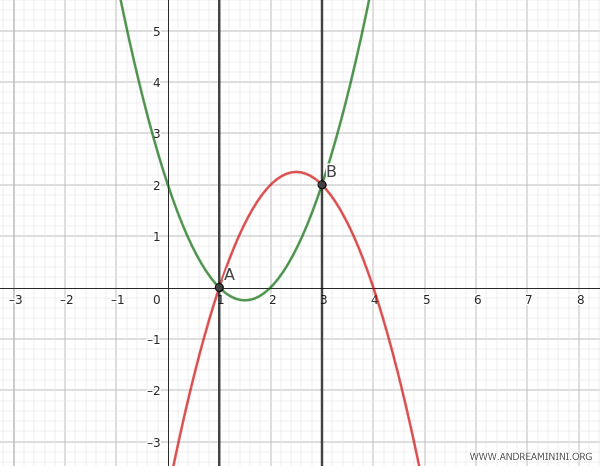
1] Primo caso
Ad esempio, il valore λ=-1 elimina la variabile y dall'equazione della parabola.
$$ (y-x^2+3x-2) + (-1) \cdot (y+x^2-5x+4) = 0 $$
$$ \require{cancel} \cancel{y}-x^2+3x-2 \cancel{-y}-x^2+5x-4) = 0 $$
$$ -2x^2+8x-6 = 0 $$
$$ -x^2+4x-3 = 0 $$
Questa equazione di 2° grado ha due soluzioni
$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
$$ x = \frac{-4 \pm \sqrt{4^2-4(-1)(-3)}}{2(-1)} $$
$$ x = \frac{-4 \pm \sqrt{16-12}}{-2} $$
$$ x = \frac{-4 \pm \sqrt{4}}{-2} $$
$$ x = \frac{-4 \pm 2}{-2} $$
$$ x = 2 \pm 1 = \begin{cases} x= 3 \\ \\ x=1 \end{cases} $$
Quindi, posso scrivere l'equazione $ -x^2+4x-3 = 0 $ come il prodotto di due rette
$$ (x-3) \cdot (x-1) = 0 $$
In altre parole, la parabola degenera in due rette parallele che passano nei punti base A e B.
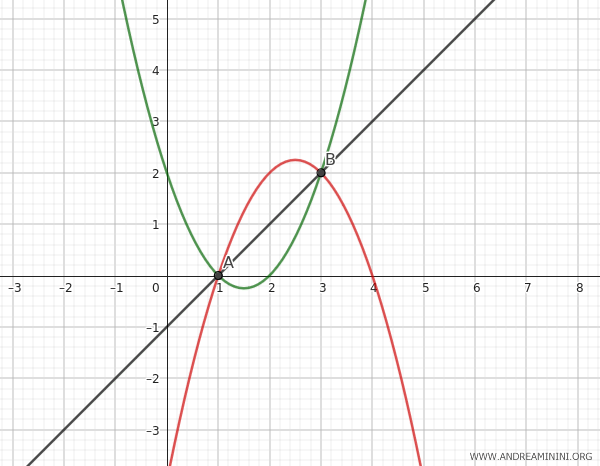
2] Secondo caso
Un'altra parabola degenere si verifica quando il parametro è λ=1 perché elimina la componente quadratica x2 dall'equazione della parobola.
$$ (y-x^2+3x-2) + (1) \cdot (y+x^2-5x+4) = 0 $$
$$ y\cancel{-x^2}+3x-2+ y+\cancel{x^2}-5x+4 = 0 $$
$$ 2y-2x+2= 0 $$
In questo caso la parabola del fascio degenera in una retta che passa per i punti base A e B.
E così via.
