Fascio di parabole che passa per due punti

Il fascio di parabole passanti per due punti distinti \( A(x_A, y_A) \) e \( B(x_B, y_B) \) può essere ottenuto con l'equazione $$ y = mx + q + \lambda (x - x_A)(x - x_B) $$ dove $ y=mx+q$ è la retta che passa per i punti mentre \( k \) è il parametro che genera le parabole del fascio.

La retta passante per i punti A e B ha equazione \( y = mx + q \), dove \( m \) è il coefficiente angolare e \( q \) è l'intercetta.

Posso trovare \( m \) e \( q \) utilizzando le coordinate di A e B:

$$  m = \frac{y_B - y_A}{x_B - x_A} $$

$$  q = y_A - m x_A $$

Sostituendo le coordinate di A e B nell'equazione, l'equazione è soddisfatta per ogni valore di \( k \).

La dimostrazione che l'equazione rappresenta un fascio di parabole si basa sul fatto che per ogni valore di \( k \), l'equazione soddisfa le coordinate di A e B e traccia una curva che varia con \( k \).

Esempio

Considero i punti $ A(1;0) $ e B(3.2).

Devo individuare l'equazione del fascio di parabole che passa per A e B.

La retta che passa per entrambi i punti è:

$ y=mx+q$

Calcolo il coefficiente angolare della retta

$$  m = \frac{y_B - y_A}{x_B - x_A} $$

$$  m = \frac{2 - 0}{3 - 1} = \frac{2}{2} $$

$$ m = 1 $$

Poi l'intercetta della retta

$$  q = y_A - m x_A $$

$$  q = 0 - 1 \cdot 1 $$

$$ q = -1 $$

Quindi, la retta è che passa tra A e B è la seguente:

$ y=x-1$

L'equazione del fascio di retta è

$$ y = mx + q + \lambda (x - x_A)(x - x_B) $$

$$ y = x - 1 + \lambda (x - 1)(x - 3) $$

Questa equazione rappresenta un insieme di parabole che passano per i punti A e B, con aperture che variano a seconda del parametro \( k \). Ogni parabola nel fascio è unica per un dato valore di \( k \).

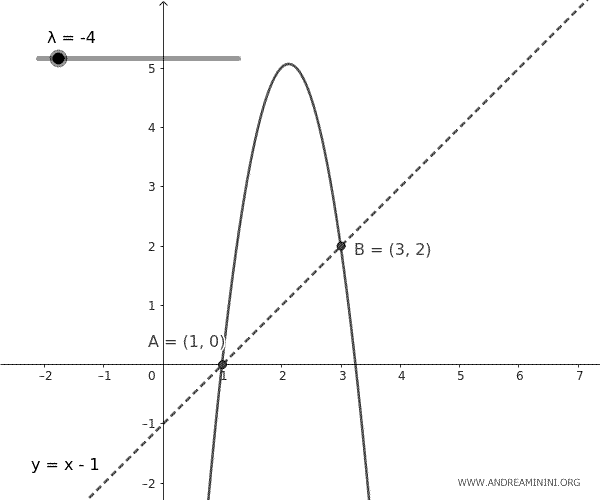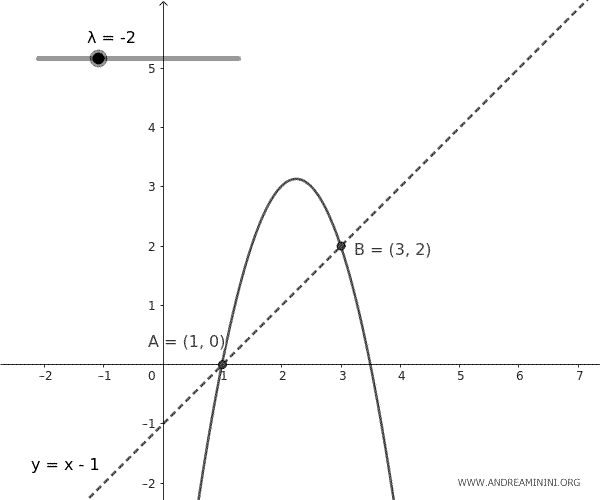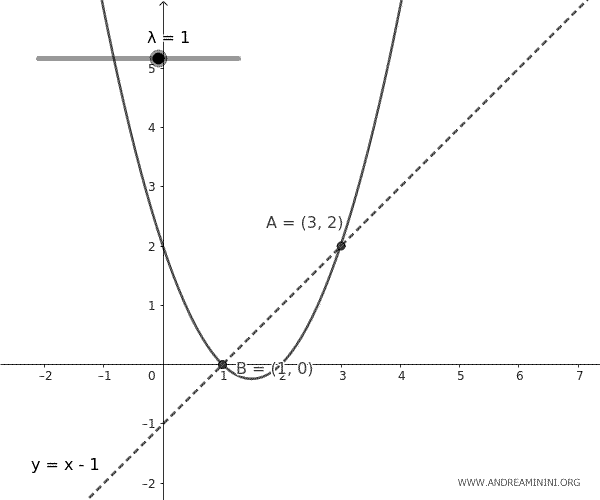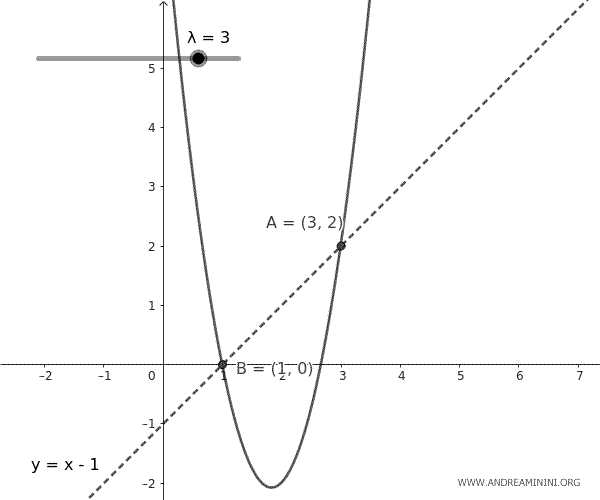
E così via.