Fascio di parabole tangenti a una retta
Un fascio di parabole tangenti nel punto \( T(x_T;y_T) \) alla retta \( r \) di equazione \( y = mx + q \), si ottiene utilizzando l'equazione $$ y = mx + q + k (x - x_T)^2 $$
Un esempio pratico
Considero una retta \( r \) che ha l'equazione
$$ y = -x + 2 $$
Prendo un punto \( T \) che appartiene alla retta è \( T(1, 1) \).
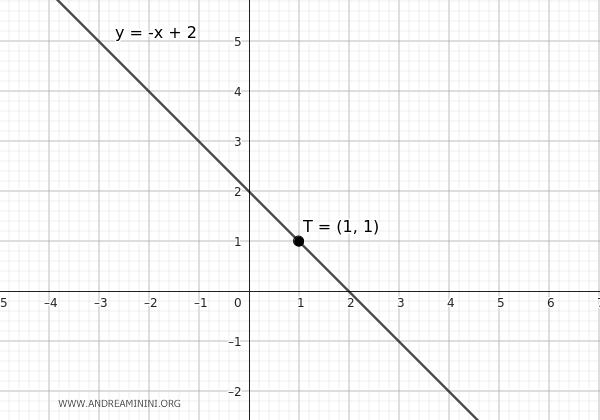
L'equazione del fascio di parabole tangenti alla retta $ r $ nel punto $ T $ è la seguente:
$$ y = mx + q + k (x - x_T)^2 $$
$$ y = -x + 2 + k (x - 1)^2 $$
Costruisco alcune parabole del fascio con diversi valori di \( k \):
Ad esempio, per $ k=1 $ ottengo l'equazione
$$ y = -x + 2 + 1 \cdot (x - 1)^2 $$
$$ y = -x + 2 + x^2-2x+1 $$
$$ y = x^2-3x + 3 $$
Ecco il grafico della parabola che effettivamente è tangente alla retta nel punto T.
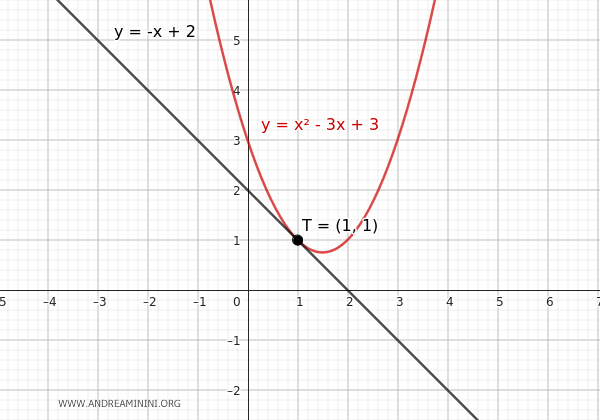
Faccio un altro esempio prendendo $ k = - 1 $
$$ y = -x + 2 - 1 \cdot (x - 1)^2 $$
$$ y = -x + 2 - x^2+2x-1 $$
$$ y = - x^2+x+1 $$
Anche il grafico di questa parabola è tangente alla retta nel punto T.
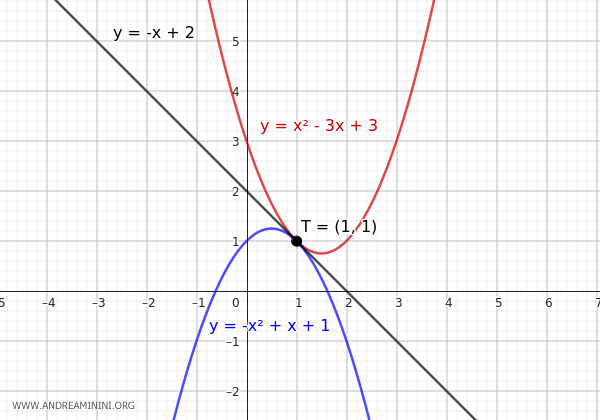
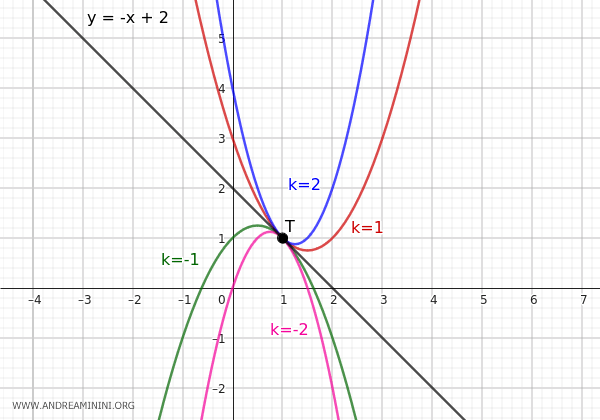
Allo stesso modo posso ottenere tutte le altre infinite parabole del fascio.
- Per \( k = 1 \) ho l'equazione \( y = x^2 - 3x + 3 \)
- Per \( k = -1 \) ho l'equazione \( y = -x^2 + x + 1 \)
- Per \( k = 2 \) ho l'equazione \( y = 2x^2 - 5x + 4 \)
Queste parabole sono tutte tangenti alla retta \( y = -x + 2 \) nel punto \( T(1, 1) \).
La dimostrazione
Per dimostrare che l'equazione \( y = mx + q + k (x - x_T)^2 \) rappresenta un fascio di parabole tangenti, prendo un punto \( T(x_T, y_T) \) della retta \( r \):**
$$ y = mx+q $$
Poiché \( T \) appartiene alla retta \( r \), anche questa equazione è soddisfatta.
$$ y_T = mx_T + q $$
Considero l'equazione:
$$ y = mx + q + k (x - x_T)^2 $$
Per essere sicuro che tutte le parabole del fascio siano tangenti alla retta \( r \) in \( T \), devmo verificare che la derivata della parabola in \( T \) sia uguale alla pendenza della retta \( r \), cioè \( m \).
Calcolo la derivata prima di \( y \) rispetto a \( x \):
$$ \frac{dy}{dx} = m + 2k(x - x_T) $$
Valuto la derivata nel punto \( T(x_T, y_T) \):
$$ \left. \frac{dy}{dx} \right|_{x = x_T} = m + 2k(x_T - x_T) = m
$$
La derivata prima della parabola nel punto \( T \) è uguale alla pendenza \( m \) della retta \( r \). Questo significa che la retta è tangente alla parabola nel punto \( T \).
Verifico che il punto \( T \) appartenga alla parabola.
Sostituisco \( x_T \) e \( y_T \) nell'equazione della parabola:
$$ y_T = mx_T + q + k(x_T - x_T)^2 = mx_T + q $$
Questo è vero poiché \( y_T = mx_T + q \), quindi il punto \( T \) appartiene anche alla parabola.
In conclusione, ho dimostrato che l'equazione \( y = mx + q + k (x - x_T)^2 \) rappresenta un fascio di parabole che sono tutte tangenti alla retta \( r: y = mx + q \) nel punto \( T(x_T, y_T) \).
E così via.
