Moto parabolico

Il moto parabolico descrive lo spostamento di un corpo materiale lungo una traiettoria parabolica.

E' anche noto come moto di un proiettile o caduta dei gravi perché descrive il comportamento di un corpo in movimento quando è soggetto all'accelerazione di gravità (g).

La caduta dei gravi

Un corpo lanciato verso l'alto ricade verso il basso con velocità variabile nel tempo.

Per misurare questo fenomeno disegno un diagramma cartesiano ponendo l'altezza sull'asse delle ordinate (y) e il tempo (t) sull'asse delle ascisse.

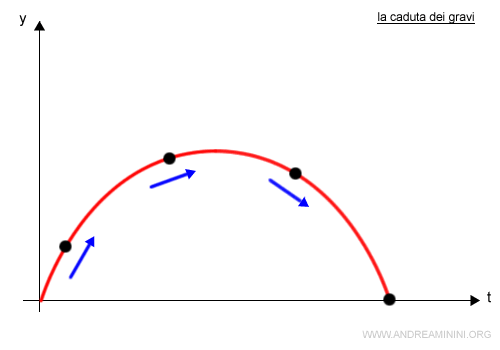
Nota. Nell'asse dell'ascise si misura il tempo (t) e non lo spazio (x). Il corpo è lanciato verso l'alto.

Durante il moto la velocità cambia continuamente per effetto della forza di gravità (g=9.8 m/sec).

Quindi, l'accelerazione del corpo è influenzata dalla forza di gravità.

$$ a(t) = -g $$

Nota. Inserisco il segno meno davanti a g perché il lancio del corpo è verso l'alto e la forza di gravità smorza la velocità nel tratto iniziale.

Integro la formula dell'accelerazione per trovare la velocità

$$ v(t) = \int a(t) \: dt = \int -g \: dt = -gt + k $$

Dove k è la velocità iniziale k=v₀ del corpo.

$$ v(t) = -gt + v_0 $$

Poi integro la formula della velocità per trovare la legge del moto.

$$ y(t) = \int v(t) \: dt = \int -gt + v_0 \: dt = -\frac{1}{2}gt^2 + v_0t + k $$

Dove k è la posizione iniziale del corpo k=y₀ rispetto all'asse y (altezza).

$$ y(t) = -\frac{1}{2}gt^2 + v_0t + y_0 $$

Qual è l'altezza massima del corpo?

In un moto parabolico l'altezza massima si raggiunge quando la velocità si annulla.

$$ v(t) = 0 $$

$$ -gt + v_0= 0 $$

Nota. Bisogna fare attenzione, la velocità si annulla in due punti, quando cambia il verso del moto e quando il corpo ricade a terra. La massima altezza si raggiunge nel primo caso.

Metto in evidenza la variabile tempo per calcolare il tempo necessario per raggiungere la massima altezza.

$$ t = \frac{v_0}{g} $$

Una volta trovato il tempo necessario (t*=t) per raggiungere l'apice, lo sostituisco nella legge del moto per trovare l'altezza massima

$$ y(t*) = -\frac{1}{2}gt*^2 + v_0t* + y_0 $$

Considero l'altezza massima h=y(t*) e t*=v₀/g

$$ h = -\frac{1}{2}g(\frac{v_0}{g})^2 + v_0 \frac{v_0}{g} + y_0 $$

$$ h = -\frac{1}{2}g \frac{v_0^2}{g^2} + \frac{v_0^2}{g} + y_0 $$

$$ h = -\frac{1}{2} \frac{v_0^2}{g} + \frac{v_0^2}{g} + y_0 $$

$$ h = \frac{1}{2} \frac{v_0^2}{g} + y_0 $$

$$ h = \frac{v_0^2}{2g} + y_0 $$

Quando il corpo raggiunge l'altezza massima si verifica l'inversione del moto.

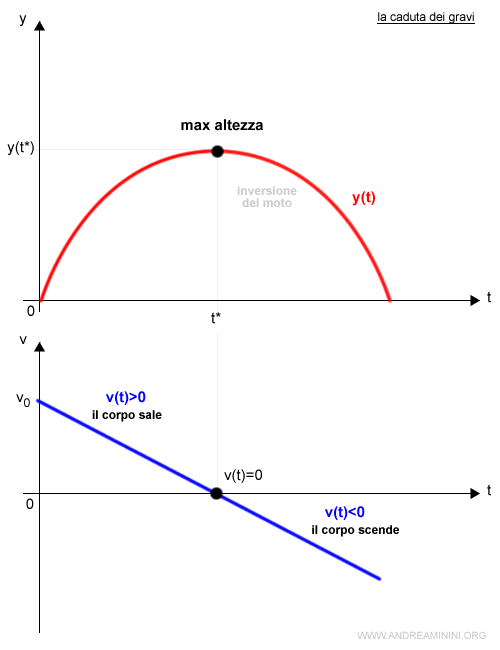
Quando il corpo lanciato in aria ritorna a terra?

Questo evento si verifica quando l'altezza è nulla ossia y(t)=0.

$$ y(t) = 0 $$

$$ -\frac{1}{2}gt^2 + v_0t + y_0 = 0 $$

Ecco la rappresentazione del moto

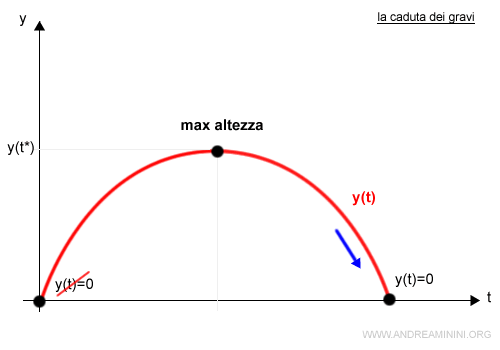
Nota. Anche in questo caso bisogna fare attenzione. Ci sono due istanti in cui l'altezza è nulla. Nel momento iniziale t=0 e nel momento finale. Per ovvi motivi non bisogna considerare il caso banale del momento iniziale (t=0).

Metto in evidenza il tempo

$$ t(v_0 -\frac{1}{2}gt) + y_0 = 0 $$

Per semplicità considero l'altezza iniziale pari a zero ossia y₀=0.

$$ t(v_0 -\frac{1}{2}gt) = 0 $$

Questa equazione si annulla quanto t=0 e quando v₀-1/2gt=0

$$ \begin{cases} t= 0 \\ \\ v_0 - \frac{1}{2gt} = 0 \end{cases} $$

Il primo caso (t=0) è il caso banale dell'istante iniziale. Pertanto, non devo considerlo.

Il secondo caso mi permette di calcolare l'istante in cui il corpo tocca nuovamente terra.

$$ v_0 - \frac{1}{2gt} = 0 $$

$$ t = \frac{2v_0}{g} $$

Ho trovato il tempo complessivo del moto del corpo dal momento iniziale (t=0) a quello finale .

Come si può notare il tempo complessivo di volo è pari al doppio del tempo di salita t*

$$ t = \frac{2v_0}{g} = 2 \cdot t* $$

Nota. Dove t* è il tempo di salita calcolato precedentemente $$ t = \frac{v_0}{g} $$

Da questo deduco che in questo caso il tempo di discesa t_D è uguale al tempo di salita t*.

Nota. Non si tratta comunque di una regola generale. In altri casi non è detto. Dipende dall'altezza in cui avviene il lancio e dall'altezza in cui avviene l'impatto del corpo sulla terra.

Pertanto, il tempo di discesa t_D del corpo è

$$ t_D = \frac{v_0}{g} $$

Qual è la velocità del corpo al momento dell'impatto?

La formula della velocità è

$$ v(t) = -gt + v_0 $$

Sostituisco t con il tempo complessivo del moto t=2v₀/g

$$ v(t) = -g ( \frac{2v_0}{g}) + v_0 $$

$$ v(t) = -2v_0 + v_0 $$

$$ v(t) = -v_0 $$

Al momento dell'impatto al suolo il corpo ha una velocità di impatto pari a -v₀.

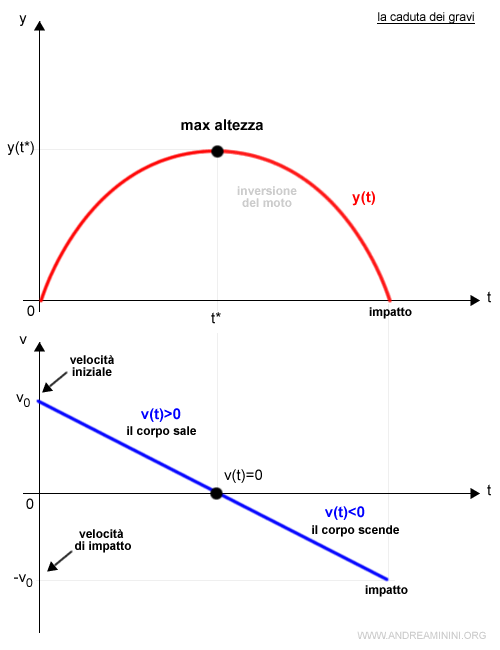
Pertanto, in questo caso la velocità di impatto è pari all'opposto della velocità iniziale (v₀).

La balistica

In questo caso il corpo si muove sia in altezza (y) che lateralmente (x).

Ad esempio, il lancio di un sasso.

La gittata è la posizione G sull'asse x in cui ricade un corpo lanciato da un'origine O.

Disegno un diagramma cartesiano ponendo l'altezza sull'asse delle ordinate (y) e la lunghezza (x) sull'asse delle ascisse.

Il corpo viene lanciato dall'origine O con una velocità v0 e un angolo a.

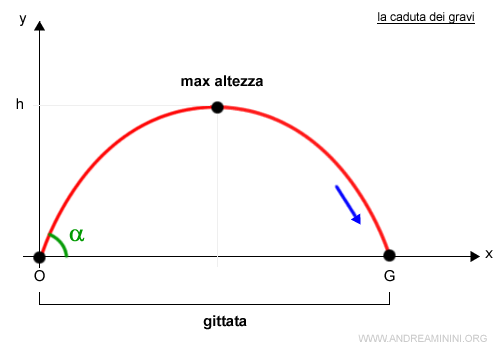
Nota. In questa analisi sull'asse orizzontale non c'è il tempo (t) bensì la lunghezza (x).

Dopo aver percorso la traiettoria parabolica, il corpo ricade nel punto G.

Il tratto OG è la gittata.

Come calcolare l'accelerazione

Questo moto è soggetto alla forza di gravità (g=9.8 m/sec)

Il vettore accelerazione del moto è

$$ \vec{a} = -g \cdot \vec{u_y} $$

Dove u_y è il versore dell'asse verticale mentre g è uno scalare pari a 9.8 m/sec (accelerazione di gravità).

Nota. La forza di gravità è una forza attrattiva che causa un'accelerazione costante verso il centro della Terra pari a -9,8 m/sec.

Come calcolare la velocità

Nota la legge dell'accelerazione a(t)=-gu_y posso ricavare la velocità per integrazione rispetto al tempo.

$$ v(t) = \int a(t) \: dt $$

$$ v(t) = \int -g \vec{u_y} \: dt $$

$$ v(t) = -g \cdot t \cdot \vec{u_y} + k $$

Dove k è la velocità iniziale v₀.

$$ v(t) = -g \cdot t \cdot \vec{u_y} + \vec{v_0} $$

La velocità iniziale v₀ è un vettore che ha origine in O e un angolo pari all'angolazione di lancio (α).

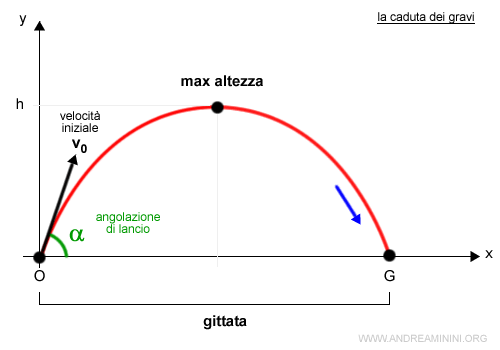
Conoscendo l'angolazione del lancio (α) posso calcolare il vettore della velocità iniziale v₀ nelle sue proiezioni sull'asse x e y

$$ \vec{v_0}=\vec{v_{0x}}+\vec{v_{0y}} $$

Dal punto di vista grafico.

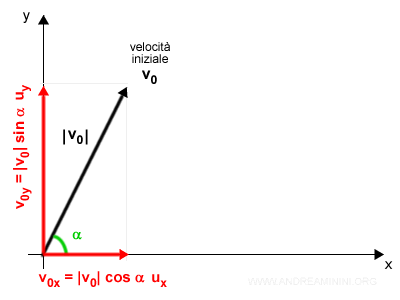
La lunghezza del vettore v₀ è il modulo |v₀|

Le proiezioni sugli assi sono

$$ \begin{cases} v_{0x} = |v_0| \cos(α) \cdot \vec{u_x} \\ \\ v_{0y} = |v_0| \sin(α) \cdot \vec{u_y} \end{cases} $$

Pertanto, la formula della velocità diventa

$$ v(t) = \vec{v_0}-gt \vec{u_y} $$

$$ v(t) = |v_0| \cdot \cos(α) \cdot u_x + |v_0| \sin(α) u_y -gt \vec{u_y} $$

$$ v(t) = |v_0| \cdot \cos(α) \cdot u_x + ( |v_0| \sin(α) -gt ) \vec{u_y} $$

A questo punto diventa importante analizzare la velocità nelle sue componenti x e y.

Perché? Durante il moto il corpo si sposta in avanti (asse x) e in alto/basso (asse y). Pertanto, si sposta con due velocità differenti v_x e v_yche sono soggette a leggi differenti poiché l'accelerazione di gravità agisce soltanto verso il basso.

Posso calcolare le velocità v_x e v_y per integrazione delle accelerazioni a_x e a_y.

Quindi, devo prima scorporare l'accelerazione in a_x e a_y.

$$ \vec{a} = -g \cdot \vec{u_y} $$

Poiché l'accelerazione (a) è uguale alla forza di gravità (-g) che agisce solo sull'asse verticale (y), ne consegue che l'accelerazione a_x=0.

$$ \begin{cases} a_x = 0 \\ \\ a_y = - g \end{cases} $$

Integro le accelerazioni a_x e a_y rispetto al tempo per calcolare le velocità v_x e v_y

$$ \begin{cases} v_x = \int a_x \: dt \\ \\ v_y = \int a_y \: dt \end{cases} $$

$$ \begin{cases} v_x = a_x \cdot t + k \\ \\ v_y = a_y \cdot t +k \end{cases} $$

Dove k è la velocità iniziale v₀ rispetto all'asse x o y

$$ \begin{cases} v_x = a_x \cdot t + v_{0x} \\ \\ v_y = a_y \cdot t + v_{0y} \end{cases} $$

Sapendo che a_x=0 e a_y=-g

$$ \begin{cases} v_x = 0 \cdot t + v_{0x} \\ \\ v_y = -g \cdot t + v_{0y} \end{cases} $$

$$ \begin{cases} v_x = v_{0x} \\ \\ v_y = -g \cdot t + v_{0y} \end{cases} $$

Infine sostituisco le velocità iniziali v_0x= v₀·cos α e v_0y= v₀·sin α

$$ \begin{cases} v_x = v_0 \cdot \cos α \\ \\ v_y = -g \cdot t + v_0 \cdot \sin α \end{cases} $$

Ho trovato le leggi della velocità del corpo nelle componenti x e y.

Come calcolare la legge del moto

E' molto semplice. Per ottenere la posizione del corpo nelle coordinate x e y mi basta integrare le leggi della velocità v_x e v_y rispetto al tempo.

$$ \begin{cases} x(t) = \int v_x \: dt \\ \\ y(t) = \int v_y \: dt \end{cases} $$

$$ \begin{cases} x(t) = \int v_0 \cdot \cos α \: dt \\ \\ y(t) = \int -g \cdot t + v_0 \cdot \sin α \: dt \end{cases} $$

$$ \begin{cases} x(t) = v_0 \cdot t \cdot \cos α + k \\ \\ y(t) = -g \cdot \frac{1}{2} t^2 + v_0 \cdot t \cdot \sin α + k \end{cases} $$

Dove k è rispettivamente la posizione iniziale x₀ e y₀ ossia la posizione (x,y) nell'istante t=0.

$$ \begin{cases} x(t) = v_0 \cdot t \cdot \cos α + x_0 \\ \\ y(t) = -g \cdot \frac{1}{2} t^2 + v_0 \cdot t \cdot \sin α + y_0 \end{cases} $$

Ho così trovato la legge del moto che determina la posizione x(t) e y(t) del corpo nello spazio al trascorrere del tempo.

Nota. Sull'asse x il moto è uniforme mentre sull'asse y il moto è uniformemente accelerato. L'equazione del moto sull'asse y è una parabola.

Per completare il lavoro posso calcolare il tempo a partire dalla prima equazione

$$ t = \frac{x}{v_0 \cos α} $$

e sostituirlo alla variabile t nella seconda equazione

$$ y(t) = -g \cdot \frac{1}{2} t^2 + v_0 \cdot t \cdot \sin α + y_0 $$

$$ y(t) = -g \cdot \frac{1}{2} ( \frac{x}{v_0 \cos α} )^2 + v_0 \cdot ( \frac{x}{v_0 \cos α} ) \cdot \sin α + y_0 $$

$$ y(t) = -g \cdot \frac{1}{2} ( \frac{x}{v_0 \cos α} )^2 + \frac{v_0}{v_0} \cdot ( \frac{\sin α}{ \cos α} ) \cdot x + y_0 $$

$$ y(t) = - \frac{1}{2} \frac{-g \cdot x^2}{ v_0^2 \cos^2 α} + \tan(α) \cdot x + y_0 $$

Come calcolare l'altezza massima

Per capire qual è l'altezza massima (h) raggiunta dal corpo nel moto parabolico devo individuare il punto in cui si inverte il moto da ascenzionale a discenzionale.

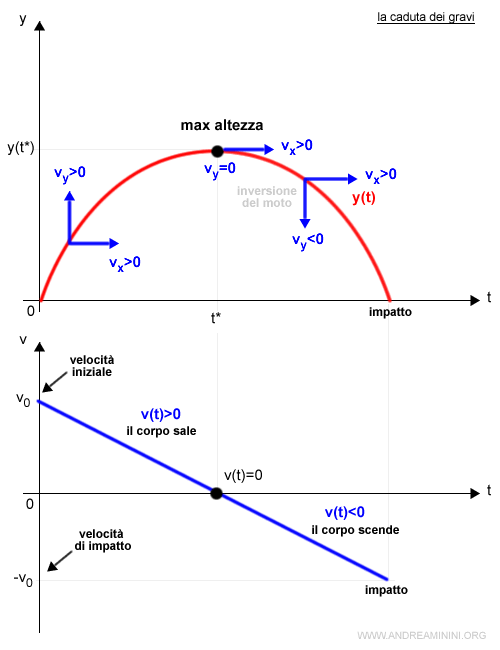
In questo punto la velocità verticale v_y si annulla.

$$ v_y=0 $$

La velocità è composta dalla somma della velocità laterale (v_x) e della velocità verticale (v_y), ossia alle proiezioni della velocità sugli assi.

Sapendo che la velocità verticale è

$$ v_y = -gt + |v_0| \sin(α) $$

Devo risolvere l'equazione

$$ v_y=0 $$

$$ -gt + |v_0| \sin(α) =0 $$

Metto in evidenza il tempo (t)

$$ t = \frac{|v_0| \sin(α)}{g} $$

Ho così trovato l'istante in cui il corpo si sposta con velocità verticale nulla

Per trovare l'altezza massima (h) sostituisco l'istante t nella legge oraria

$$ y(t) = -g \cdot \frac{1}{2} t^2 + v_0 \cdot t \cdot \sin(α) + y_0 $$

In questo modo l'altezza y(t) è l'altezza massima h

$$ h = -g \cdot \frac{1}{2} (\frac{v_0 \sin(α)}{g})^2 + v_0 \cdot (\frac{v_0 \sin(α)}{g}) \cdot \sin(α) + y_0 $$

$$ h = -g \cdot \frac{1}{2} \frac{v_0^2 \sin^2(α)}{g^2} + \frac{v_0^2 \sin^2(α)}{g} + y_0 $$

$$ h = -\frac{1}{2} \frac{g \cdot v_0^2 \sin^2(α)}{g^2} + \frac{v_0^2 \sin^2(α)}{g} + y_0 $$

$$ h = -\frac{1}{2} \frac{v_0^2 \sin^2(α)}{g} + \frac{v_0^2 \sin^2(α)}{g} + y_0 $$

$$ h = \frac{1}{2} \frac{v_0^2 \sin^2(α)}{g} + y_0 $$

Ho così trovato l'altezza massima (h) del corpo.

Quale angolo (α) di lancio raggiunge l'altezza massima?

Basta osservare la formula.

$$ h = \frac{1}{2} \frac{v_0^2 \sin^2(α)}{g} + y_0 $$

Dove v₀, y₀ e g sono costanti.

Resta da analizzare la componente sin²(α) che raggiunge il suo valore massimo quando l'angolo è 90° ossia α=π/2.

Quindi, ceteris paribus, l'angolo che massimizza l'altezza è α=90° ossia un lancio verso l'alto senza spostamento orizzontale.

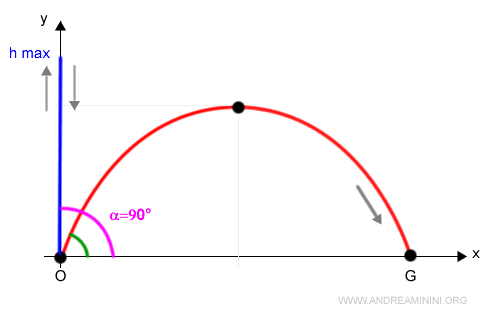
Come calcolare la gittata

Per calcolare la gittata devo trovare il tempo di volo necessario per raggiungere un'altezza h=0 ossia y=0.

$$ y=0 $$

Per semplicità ipotizzo che il lancio avvenga dall'altezza zero y₀=0.

In questo caso la legge del moto verticale è

$$ y = v_0 \cdot t \cdot \sin(α)- \frac{1}{2} gt^2 $$

Pertanto, l'equazione y=0 diventa

$$ y = 0 $$

$$ v_0 \cdot t \cdot \sin(α)- \frac{1}{2} gt^2 = 0 $$

$$ t \cdot ( v_0 \sin(α)- \frac{1}{2} gt^2 ) = 0 $$

Questa equazione ha due soluzioni

$$ \begin{cases} t=0 \\ \\ t = 2 v_0 \frac{\sin(α)}{g} \end{cases} $$

La prima soluzione t=0 è banale perché si tratta dell'istante iniziale.

La seconda soluzione è, invece, l'istante in cui avviene l'impatto al suolo ed è quella che mi serve.

Una volta ottenuto il tempo di volo, posso applicarlo alla legge del moto orizzontale.

$$ x = v_0 \cdot t \cdot \cos(α) $$

$$ x = v_0 \cdot ( 2 v_0 \frac{\sin(α)}{g} ) \cos(α) $$

$$ x = 2 v_0^2 \frac{\sin(α)}{g} \cos(α) $$

$$ x = v_0^2 \cdot ( 2 \cdot \sin(α) \cdot \cos(α) ) \cdot \frac{1}{g} $$

Nota. Dalle formule della trigonometria so che $$ 2 \cdot \sin(α) \cdot \cos(α) = \sin(2α) $$

$$ x = v_0^2 \cdot \sin(2α) \cdot \frac{1}{g} $$

$$ x = \frac{ v_0^2 \cdot \sin(2α) } { g } $$

Ho così trovato la gittata del lancio.

Come trovare la gittata massima

In questo caso il problema consiste nel trovare l'angolo (α) che massimizza la gittata.

Sapendo che la formula della gittata è

$$ L = \frac{v_0^2 \cdot \sin(2α)}{g} $$

Dove v₀ e g sono costanti. Quindi, resta da analizzare la componente seno sin(2α).

La funzione trigonometrica del seno varia da -1 a 1.

Il valore massimo del seno è 1 ed è raggiunto quando l'argomento del seno è 90° ossia π/2.

In questo caso l'argomento è 2α

$$ 2α = π/2 $$

$$ α = π/4 $$

Dove π/4 è un angolo di 45°

$$ α = 45° $$

Pertanto, la gittata massima si raggiunge con un angolo (α) di 45°.

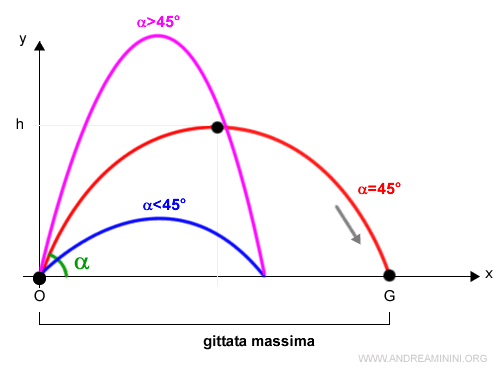
Al di sopra e al di sotto di 45° la gittata è inferiore.

E così via.