La distribuzione della velocitÓ di Maxwell e Boltzmann
La curva di Maxwell e Boltzmann misura la distribuzione della velocità delle molecole di un gas.
Nella metà del XIX secolo si cominciò a indagare sulla velocità delle particelle di un gas tramite gli strumenti dell'indagine statistica.
Prima Maxwell e poi Boltzmann giunsero a conclusioni simili.
Anche un piccolo volume di gas è composto da migliaia di particelle, ognuna delle quali si muove con una velocità differente.
Tuttavia, gran parte delle particelle si muovono con una velocità vicina alla velocità media.
La distribuzione delle velocità delle particelle del gas può essere rappresentata con una curva a campana asimmetrica.
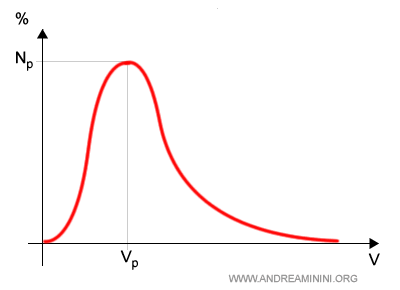
Dove Np è la percentuale di particelle del gas che probabilmente si muovono alla velocità Vp.
L'area compresa tra l'asse orizzontale delle ascisse e la curva equivale al numero totale N delle particelle del gas.
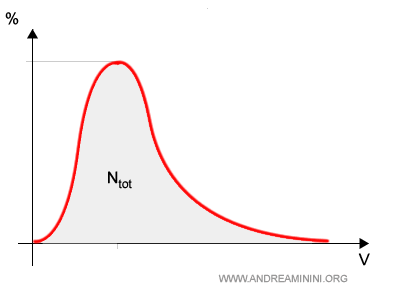
Dal grafico si capisce subito che le particelle con velocità estreme, molto alte (v2) o molto basse (v1), sono relativamente poche.
La maggior parte delle particelle ha una velocità compresa nell'intorno del punto di massimo della curva.
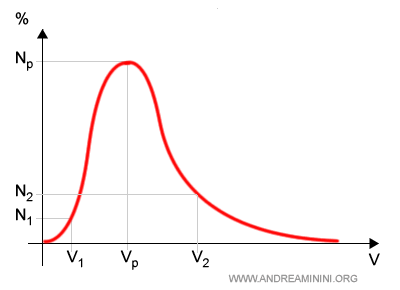
Il picco della curva indica il valore più probabile della velocità delle particelle.
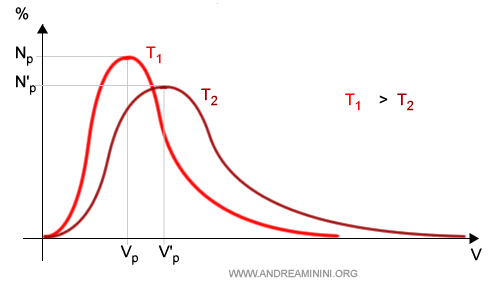
Al variare della temperatura la curva cambia posizione e forma
- Se la temperatura aumenta, la curva si sposta in alto a destra, si allunga e il picco si abbassa. La velocità media delle particelle aumenta ma la percentuale delle particelle nell'intorno si riduce. Meno particelle si muovono con una velocità simile alla velocità media.
- Se la temperatura si riduce, la curva si sposta in basso a sinistra, si accorcia e il picco si alza. La velocità media delle particelle diminuisce ma la percentuale delle particelle nell'intorno aumenta. Più particelle si muovono con una velocità simile alla velocità media.
Spesso più che la percentuale Np di particelle con una particolare velocità, si calcola la percentuale di particelle con una determinata energia cinetica.
L'energia cinetica media delle particelle è
$$ E_c = \frac{1}{2} mv^2 $$
Dove m è la massa e v è la velocità.
La percentuale di particelle con energia cinetica superiore alla media Ec è uguale al seguente esponenziale
$$ N \cdot e^{-E/RT} $$
Dove N è il numero totale delle particelle, R è la costante universale dei gas, T è la temperatura.
Quindi, la percentuale di particelle con energia cinetica superiore alla media cresce in modo esponenziale quando aumenta la temperatura (T) del gas.
Questa formula è la rappresentazione matematica delle curve di Maxwell-Boltzmann.
E così via.
