Le funzioni crescenti e decrescenti

Per verificare se una funzione è crescente o decrescente, si può usare il criterio di monotonia delle funzioni in base al quale c'è una relazione tra la derivata prima della funzione f(x) e la crescenza o decrescenza della funzione stessa.

Funzione crescente

Una funzione f(x) continua in [a,b] e derivabile in (a,b) è crescente in [a,b] se la derivata prima f(x) è maggiore uguale a zero $$ f'(x) \ge 0 $$ per ogni x ∈ (a,b).

Funzione decrescente

Una funzione f(x) continua in [a,b] e derivabile in (a,b) è decrescente in [a,b] se la derivata prima f(x) è minore uguale a zero $$ f'(x) \le 0 $$ per ogni x ∈ (a,b).

A cosa serve?

Il segno della derivata prima f'(x) è una delle principali informazioni nello studio e nella costruzione del grafico di una funzione.

Un esempio pratico

Ho la funzione x²

$$ f(x)=x^2 $$

La derivata prima della funzione è

$$ f'(x)=2x $$

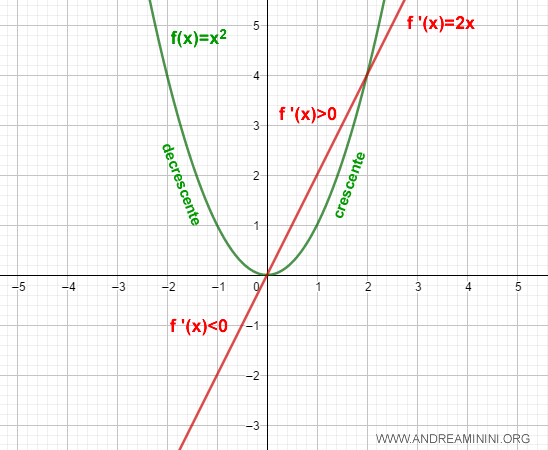
Da -∞ a 0 la funzione derivata f'(x)=2x è negativa, mentre da 0 a +∞ è positiva.

$$ f'(x)= \begin{cases} 2x > 0 \text{ se x>0 } \\ 2x < 0 \text{ se x<0 } \end{cases} $$

Pertanto, la funzione f(x)=x² è decrescente nell'intervallo (-∞,0) e crescente nell'intervallo (0,∞)

Dimostrazione e spiegazione

Ipotesi 1 ( derivata prima positiva )

Comincio la dimostrazione con l'ipotesi che la funzione derivata prima f'(x) sia non negativa nell'intervallo (a,b)

$$ f'(x) \ge 0 $$

Devo verificare se è crescente o decrescente.

Prendo due punti intermedi x₁ e x₂ dell'intervallo (a,b) tali che

$$ a \le x_1 \le x_2 \le b $$

Se la funzione è crescente deve valere la seguente relazione

$$ f(a) \le f(x_1) \le f(x_2) \le f(b) $$

Secondo il teorema di Lagrange nell'intervallo (x₁,x₂) deve esistere un punto x₀ in cui

$$ f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1} $$

con un semplice passaggio algebrico

$$ f(x_2)-f(x_1) = f'(x_0) \cdot (x_2-x_1) $$

Poiché f'(x₀)≥0 per ipotesi e (x₂-x₁)>0 perché x₂>x₁ allora anche la differenza f(x₂)-f(x₁)≥0

$$ f(x_2)-f(x_1) \ge 0 $$

Pertanto, la funzione nell'intervallo (x₁,x₂) è crescente.

Questo dimostra la relazione tra la derivata prima positiva e la crescenza della funzione.

Nota. La relazione tra la derivata prima f'(x)≤0 (non positiva) e la decrescenza della funzione f(x) si dimostra in modo analogo ponendo per ipotesi f'(x)≤0. In questo caso, essendo (x₂-x₁)>0 la differenza f(x₂)-f(x₁)≤0

Ipotesi 2 ( funzione crescente )

Ipotizzo che la funzione sia crescente nell'intervallo (a,b) senza sapere nulla della derivata.

Quindi, preso un punto x₀∈(a,b) la funzione è crescente in x₀.

Per conoscere la derivata della funzione nel punto, calcolo il limite del rapporto incrementale della funzione in x₀.

$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

Essendo una funzione crescente il numeratore del rapporto incrementale è

• f(x+h)-f(x) ≥0 per h>0
• f(x+h)-f(x) ≤0 per h<0

Quindi il rapporto incrementale è maggiore o uguale a zero sia per h>0 nella derivata destra

$$ f'(x_0+) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

che per h<0 nella derivata sinistra

$$ f'(x_0-) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

Nota. Nella derivata sinistra il denominatore (h<0) del rapporto incrementale è un valore negativo. Essendo minore o uguale a zero anche il numeratore f(x-h)-f(x) ≤0, il quoziente del rapporto è sicuramente un valore positivo.

Quindi la derivata prima della funzione nel punto x₀ è positiva.

$$ f'(x_0) \ge 0 $$

E così via.