Equazione di Clapeyron
L'equazione di Clapeyron misura la variazione della pressione e della temperatura nella curva di equilibrio dinamico tra due fasi di una sostanza. $$ \log \frac{P_1}{P_2} = - \frac{\Delta H}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
E' anche conosciuta come equazione di Clausius-Clapeyron.
Dove P è la pressione, H è l'entalpia (es. entalpia di evaporazione), T è la temperatura assoluta, R è la costante universale dei gas.
Nota. Il logaritmo nella formula è il logaritmo naturale (ln) poiché non è specificato nulla.
A cosa serve l'equazione di Clapeyron
L'equazione è utile per misurare i cambiamenti nelle transizioni di fase (es. liquido-vapore, solido-liquido, solido-vapore).
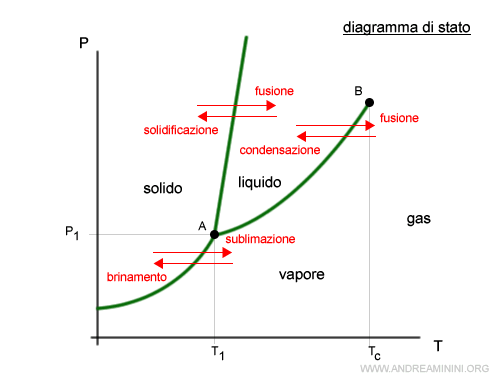
Dal punto di vista grafico, l'equilibrio dinamico di verifica lungo la curva che separa due fasi in un diagramma di stato.
La dimostrazione
Prendo in considerazione un punto (P1,T1) nella curva del diagramma di stato che delinea il confine tra le fasi vapore e liquido.
In equilibrio dinamico tra due fasi l'energia libera della fase liquida (GL) è uguale a quella della fase vapore (GV).
$$ \Delta G = G_V - G_L = 0 $$
ossia
$$ G_V = G_L $$
Nel punto (P1,T1) la curva del diagramma di stato ha inclinazione pari a dP/dT.
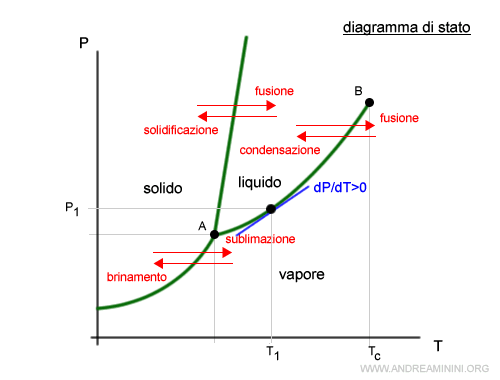
Ora mi sposto di un infinitesimo sulla curva di equilibrio (P1+dP,T1+dT).
Poiché mi sposto tra due punti in equilibrio dinamico, dopo la variazione l'energia libera del vapore deve ancora eguagliare quella del liquido (GV=DL).
Pertanto, la variazione infinitesimale delle energia libera del vapore e del liquido è uguale.
$$ dG_V = dG_L $$
Sapendo che la condizione di stabilità dell'equilibrio dinamico è dG=V(dP)-S(dT) scrivo le formule dell'energia libera mettendo in pedice lo stato di aggregazione (V=vapore, L=liquido) della sostanza.
$$ dG_V = V_V(dP)-S_V(dT) $$
$$ dG_L = V_L(dP)-S_L(dT) $$
Posso riscrivere l'equazione precedente in questo modo:
$$ dG_V = dG_L $$
$$ V_V(dP)-S_V(dT) = V_L(dP)-S_L(dT) $$
Raggruppo per dP e dT
$$ V_V(dP)-V_L(dP) = S_V(dT) -S_L(dT) $$
$$ dP(V_V-V_L) = dT(S_V-S_L) $$
Con un ulteriore passaggio algebrico metto in evidenza la relazione dP/dT
$$ \frac{dP}{dT} = \frac{S_V-S_L}{V_V-V_L} $$
Al secondo membro la differenza SV-SL misura ka variazione dell'entropia ΔS, mentre la differenza VV-VL la variazione del volume.
$$ \frac{dP}{dT} = \frac{\Delta S}{\Delta V} $$
Sapendo che la variazione dell'entropia è ΔS=ΔHEV/T
$$ \frac{dP}{dT} = \frac{\frac{\Delta H_{EV}}{T}}{\Delta V} $$
E sapendo che, in base all'equazione generale dei gas, la variazione del volume è ΔV=RT/P
$$ \frac{dP}{dT} = \frac{\frac{\Delta H_{EV}}{T}}{\frac{RT}{P} } $$
$$ \frac{dP}{dT} = \frac{\Delta H_{EV}}{T} \cdot \frac{P}{RT} $$
$$ \frac{dP}{dT} = \frac{P \cdot \Delta H_{EV}}{RT^2} $$
Poi metto in evidenza i rapporti dP/P e dT/T2
$$ \frac{dP}{P} = \frac{dT \cdot \Delta H_{EV}}{RT^2} $$
$$ \frac{dP}{P} = \frac{\Delta H_{EV}}{R} \cdot \frac{dT}{T^2} $$
Ora, in entrambi i membri dell'equazione calcolo l'integrale tra due temperature T1 e T2 a cui corrispondono in equilibrio dinamico due pressioni P1 e P2.
$$ \int_{P_1}^{P2} \frac{dP}{P} = \int_{T_1}^{T2} \frac{\Delta H_{EV}}{R} \cdot \frac{dT}{T^2} $$
I termini R e HEV sono costanti ed escono dall'integrale.
$$ \int_{P_1}^{P2} \frac{dP}{P} = \frac{\Delta H_{EV}}{R} \cdot \int_{T_1}^{T2} \frac{1}{T^2} dT $$
La primitiva del rapporto 1/T2 è la funzione -1/T perché la derivata di D[-1/T]=1/T2
Quindi, applico la formula fondamentale del calcolo integrale al secondo membro dell'equazione
$$ \int_{P_1}^{P2} \frac{dP}{P} = \frac{\Delta H_{EV}}{R} \cdot [ - \frac{1}{T} ]_{T_1}^{T_2} $$
$$ \int_{P_1}^{P2} \frac{dP}{P} = \frac{\Delta H_{EV}}{R} \cdot ( - \frac{1}{T_2} - ( - \frac{1}{T_1} ) ) $$
$$ \int_{P_1}^{P2} \frac{dP}{P} = \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
Al primo membro dell'equazione la primitiva di 1/P è la funzione log P perché la derivata del logaritmo naturale D[log P]=1/P.
Anche in questo caso applico la formula fondamentale del calcolo integrale.
$$ [ \log P ]^{P_2}_{P_1} = \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
$$ \log P_2 - \log P_1 = \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
Moltiplico entrambi i membri per -1
$$ (-1) \cdot ( \log P_2 - \log P_1 )= (-1) \cdot \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
$$ \log P_1 - \log P_2 = - \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
Per le proprietà dei logaritmi, la differenza tra due logaritmi è uguale al logaritmo rapporto.
Quindi log P1 - log P2 si può scrivere anche log P1/P2.
$$ \log \frac{P_1}{P_2} = - \frac{\Delta H_{EV}}{R} \cdot ( \frac{1}{T_1} - \frac{1}{T_2} ) $$
Ho così ottenuto la formula dell'equazione di Clausius-Clapeyron.
E così via.
