Raggruppamento
Un raggruppamento indica quanti gruppi diversi si possono formare scegliendo un elemento da ciascuno di due o più insiemi.
In generale, se il primo insieme ha \( n \) elementi, il secondo ne ha \( m \), il terzo \( k \), e così via, allora il numero totale dei gruppi che posso formare è:
\[ n \cdot m \cdot k \]
Si moltiplica perché ogni elemento del primo insieme può essere combinato con tutti quelli del secondo, poi con tutti quelli del terzo, e così via.
Un esempio pratico
Considero due insiemi A e B
- insieme \( A = \{ a_1, a_2, a_3 \} \) con 3 elementi
- insieme \( B = \{ b_1, b_2 \} \) con 2 elementi
Un raggruppamento consiste nel formare un gruppo scegliendo un elemento da ( A ) e uno da ( B ).
I gruppi possibili sono:
$$ (a_1, b_1) \\ (a_1, b_2) \\ (a_2, b_1) \\ (a_2, b_2) \\ (a_3, b_1) \\ (a_3, b_2) $$
In totale ci sono sei raggruppamenti
$$ 3 \cdot 2 = 6 $$
L’esempio mostra chiaramente che ogni elemento di \( A \) può abbinarsi con ciascun elemento di \( B \), e per questo si moltiplica.
Esempio 2
In questo esempio considero tre insiemi A, B e C.
- insieme \( A = \{ a_1, a_2 \} \) con 2 elementi
- insieme \( B = \{ b_1, b_2, b_3 \} \) con 3 elementi
- insieme \( C = \{ c_1, c_2 \} \) con 2 elementi
Un raggruppamento consiste nel formare un gruppo scegliendo un elemento da \( A \), uno da \( B \) e uno da \( C \).
I gruppi possibili sono \( (a_i, b_j, c_k) \) che elencati concretamente sono:
$$ (a_1, b_1, c_1) \\ (a_1, b_1, c_2) \\ (a_1, b_2, c_1) \\ (a_1, b_2, c_2) \\ (a_1, b_3, c_1) \\ (a_1, b_3, c_2) \\ (a_2, b_1, c_1) \\ (a_2, b_1, c_2) \\ (a_2, b_2, c_1) \\ (a_2, b_2, c_2) \\ (a_2, b_3, c_1) \\ (a_2, b_3, c_2) $$
Quindi si possono formare dodici raggruppamenti.
$$ 2 \cdot 3 \cdot 2 = 12 $$
Un modo per rappresentare graficamente il numero di tutti i gruppi che si possono formare è il diagramma ad albero.
In un diagramma ad albero ogni insieme corrisponde a un livello dell’albero.
In questo caso il diagramma ad albero presenta due ramificazioni iniziali, corrispondenti ai due elementi del primo insieme
\( A = \{ a_1, a_2 \} \).
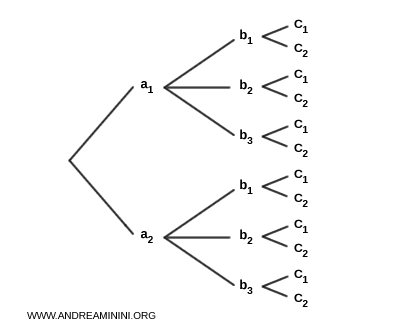
Da ciascuna di queste si diramano tre ramificazioni di secondo livello, una per ogni elemento del secondo insieme \( B = \{ b_1, b_2, b_3 \} \).
Infine, da ciascuna ramificazione di secondo livello si diramano altre due ramificazioni di terzo livello, una per ciascun elemento del terzo insieme \( C = \{ c_1, c_2 \} \) .
Nota. In generale, da ogni elemento del primo insieme partono tante “ramificazioni” quante sono le scelte del secondo insieme, e da ciascuna di queste partono le ramificazioni per il terzo insieme, e via dicendo.
E così via.
