Le permutazioni
Una permutazione è una corrispondenza biunivoca di un insieme con se stesso. Un insieme con n elementi ha n! (n fattoriale) permutazioni. $$ n! = n \cdot (n-1) \cdot (n-2) \cdot \cdot \cdot 3 \cdot 2 \cdot 1 $$ Dove n! si legge n fattoriale e $ n>1 $.
In altre parole, le permutazioni semplici di n elementi distinti sono tutti i gruppi formati dagli n elementi che differiscono tra loro solo per la posizione ossia per l'ordine in cui sono disposti.
Il numero totale delle permutazioni semplici di un insieme di n elementi è dato dalla seguente formula
$$ P_n = n! = n \cdot (n-1) \cdot ... \cdot 2 \cdot 1 $$
Per definizione se n è uguale 0, il valore n! è 1.
$$ 0!=1 $$
È importante sottolineare che, in una permutazione semplice, tutti gli elementi dell’insieme devono essere utilizzati una e una sola volta. Non è ammessa la ripetizione di un elemento e non è possibile ometterne uno.
Esempio. Quante parole posso formare usando solo le lettere A, B, C una e una sola volta? In questo caso, il numero delle permutazioni semplici è $ n! = 3 \cdot 2 \cdot 1 = 6 $. Quindi, posso formare sei permutazioni semplici. $$ ABC, ACB, BAC, BCA, CAB, CBA $$ In ogni permutazione compaiono le lettere A, B, C tutte presenti e tutte in posizioni distinte.
Se l'insieme di riferimento contiene elementi ripetuti, il numero delle permutazioni con ripetizione si calcolano usando questa formula.
$$ P_n^{(h,k,..)} = \frac{ n! }{ h! k! ... } $$
Esempio. Quante parole posso formare usando solo le lettere della parola "ANNA". In questo caso, le lettere sono 4, quindi le possibili disposizioni sono: $ n! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $. Se le lettere fossero tutte diverse, queste 24 disposizioni sarebbero 24 parole differenti. Ma nella parola ANNA le lettere si ripetono, quindi molte delle 24 combinazioni coincidono tra loro. Ad esempio, “ANNA” compare più volte, “ANAN” compare più volte, “AANN” compare più volte, e così via. Ecco un elenco che mostra chiaramente le ripetizioni:
ANNA, ANAN, ANNA, ANAN, AANN, AANN
NANA, NAAN, NNAA, NNAA, NAAN, NANA
NANA, NAAN, NNAA, NNAA, NANA, NAAN
AANN, AANN, ANAN, ANNA, ANAN, ANNA
Osservando l'elenco, si vede che le parole davvero diverse sono molte meno delle 24 iniziali. Questo succede perché scambiare due lettere identiche non produce una nuova parola. Per contare solo le parole uniche si calcolano le permutazioni con ripetuzione. Nella parola ANNA la lettera A compare 2 volte ( $ h=2 $ ) e anche la lettera N compare 2 volte ( $ k=2 $ ). Quindi, le permutazioni con ripetizione sono: $$ P_n^{(h,k,..)} = \frac{ 4! }{ 2! \cdot 2! ... } = \frac{24}{4} = 6 $$ Pertanto, ci sono 6 parole uniche tra i 24 anagrammi e sono le seguenti:
ANNA, ANAN, AANN, NANA, NAAN, NNAA
Un esempio pratico
Dato un insieme X con 5 elementi
$$ X = \{ a,b,c,d,e \} $$
Sono permutazioni le seguenti:
$$ a,b,c,d,e \\ b,a,c,d,e \\ c,d,b,a,e \\ e,a,c,b,d \\ \vdots $$
Ogni permutazione è un insieme di corrispondenze biunivoche tra gli elementi dell'insieme X
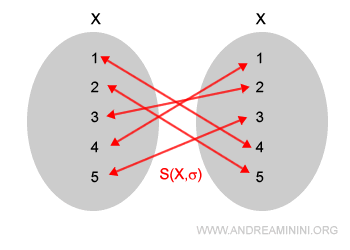
Nota. L'insieme di tutte le permutazioni è indicato con S(X). Ogni elemento dell'insieme S(X) è una composizione di applicazioni che determina una particolare permutazione. L'insieme S(x) e la composizione σ determinano una struttura algebrica detta gruppo.
L'insieme A ha cardinalità uguale a cinque perché ha 5 elementi
$$ n=5 $$
Quindi, l'insieme A ha centoventi permutazioni
$$ 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$
In questo caso n!=120
Come rappresentare le permutazioni
Posso rappresentare le permutazioni di un insieme X in vari modi.
In generale, qualsiasi insieme X posso indicarlo con dei numeri da 1 a n dove n è il numero degli elementi dell'insieme X.
Ad esempio, l'insieme X è composto da n=5 lettere
$$ X = \{ a,b,c,d,e \} $$
Sostituisco a con 1, b con 2, ecc.
$$ X = \{ 1,2,3,4,5 \} $$
E' sempre lo stesso insieme ma rappresentato in modo diverso.
Nota. In questo modo evito di scrivere quali sono gli elementi dell'insieme. Mi basta ricordare che 1=a, 2=b, 3=c, 4=d, 5=e. Dal punto di vista logico-matematico un insieme finito con n elementi è sempre lo stesso indipendentemente dalla natura degli oggetti. Poco importa se sono lettere, colori, libri, ecc.
Per rappresentare una permutazione degli elementi dell'insieme X posso usare questa forma tabellare.
$$ p = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ i_1 & i_2 & i_3 & i_4 & i_5 \end{pmatrix} $$
Nella prima riga indico gli elementi ordinati in modo crescente.
Nella seconda riga scrivo la permutazione degli elementi.
Un esempio di permutazione è la seguente
$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix} $$
La permutazione semplice p1 è una sequenza degli stessi elementi ordinati in modo differente.
Ovviamente, questa è soltanto una delle permutazioni possibili.
L'insieme X ha n!=5!=5·4·3·2·1=120 permutazioni.
Un'altra permutazione è la seguente
$$ p_2 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 5 & 3 & 1 \end{pmatrix} $$
Nella prima riga indico sempre gli elementi dell'insieme X ordinati in modo crescente.
Nella seconda riga indico la permutazione p2. La disposizione degli elementi è differente rispetto permutazione precedente.
In generale la prima riga è sempre uguale, quindi posso anche ometterla.
Pertanto, posso scrivere le stesse permutazioni anche in forma sintetica.
$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix} = (2,3,1,5,4) $$
$$ p_2 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 5 & 3 & 1 \end{pmatrix} = (4,2,5,3,1) $$
Nella forma sintetica scrivo solo la seconda riga tra parentesi tonde. La prima riga è implicita dalla posizione degli elementi.
Ad esempio, nella permutazione p1=(2,3,1,5,4) il numero 2 si trova nella prima posizione, quindi la permutazione è tra 1→2. Il numero 3 si trova nella seconda posizione, quindi la permutazione è tra 2→3
$$ p_1 : X \rightarrow X $$
$$ \\ 1 \rightarrow 2 $$
$$ \\ 2 \rightarrow 3 $$
$$ \\ 3 \rightarrow 1 $$
$$ \\ 4 \rightarrow 5 $$
$$ \\ 5 \rightarrow 4 $$
Nella permutazione p2=(4,2,5,3,1) il numero 4 è nella prima posizione, quindi la permutazione è tra 1→4. Il numero 2 si trova nella seconda posizione, quindi la permutazione è tra 2→2
$$ p_2 : X \rightarrow X $$
$$ \\ 1 \rightarrow 4 $$
$$ \\ 2 \rightarrow 2 $$
$$ \\ 3 \rightarrow 5 $$
$$ \\ 4 \rightarrow 3 $$
$$ \\ 5 \rightarrow 1 $$
Posso rappresentare le due permutazioni anche in una forma ulteriormente più sintetica come prodotto di cicli disgiunti.
Cos'è un ciclo? Un ciclo è una sequenza di passaggi che a partire da un elemento x passa per altri elementi dell'insieme e infine torna all'elemento x. Due cicli sono disgiunti se non hanno elementi in comune.
Ad esempio, nella permutazione p1=(2,3,1,5,4) ci sono due cicli disgiunti
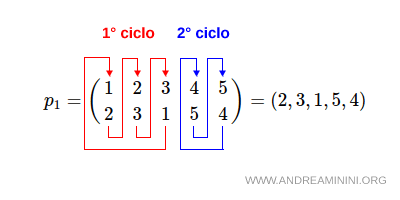
Il primo ciclo (rosso) è il seguente
$$ 1 \rightarrow 2 \rightarrow 3 \rightarrow 1 $$
Scrivo questo ciclo scrivendo tra parentesi tonde gli elementi (1,2,3)
Il secondo ciclo (blu) è il seguente
$$ 4 \rightarrow 5 \rightarrow 4 $$
Scrivo questo ciclo scrivendo tra parentesi tonde gli elementi (4,5)
Nota. Sono due cicli disgiunti perché non hanno in comune nessun elemento.
Il prodotto dei due cicli disgiunti è (1,2,3)(4,5).
Quindi posso scrivere la permutazione p1=(2,3,1,5,4) anche in questo modo
$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix} = (2,3,1,5,4) = (1,2,3)(4,5) $$
Sono modi diversi per indicare la stessa permutazione.
La notazione come prodotto di cicli disgiunti è la più sintetica possibile per rappresentare una permutazione perché omette gli elementi che non generano dei cicli.
Nota. Seguendo lo stesso criterio posso rappresentare anche la permutazione p2=(4,2,5,3,1) come prodotto di cicli disgiunti.
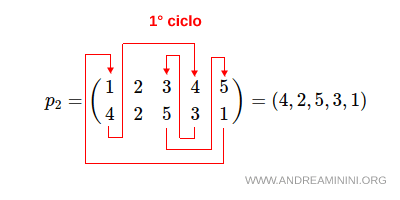
In questo caso però c'è un solo ciclo disgiunto 1→4→3→5→1 che posso scrivere nella forma (1,4,3,5). L'elemento 2→2 è sempre nella stessa posizione, quindi non forma un ciclo e posso ometterlo. Pertanto, in questo caso la rappresentazione della permutazione come prodotto di cicli disgiunti è semplicemente (1,4,3,5) senza indicare il 2 $$ p_2 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 5 & 3 & 1 \end{pmatrix} = (4,2,5,3,1) = (1,4,3,5) $$ Non vedendo il 2 nel prodotto di cicli disgiunti (1,4,3,5) capisco che il numero 2 è in corrispondenza con se stesso 2→2.
Un altro modo per rappresentare la permutazione è come prodotto di trasposizioni.
Ogni ciclo può essere scomposto in un prodotto di trasposizioni.
$$ (1,2,3...,m) = (1, m) \cdot (1,m-1) \cdot ... \cdot (1,3) \cdot (1,2) $$
Cos'è una trasposizione? E' un ciclo di ordine 2 che coinvolge due elementi e li scambia di posto.
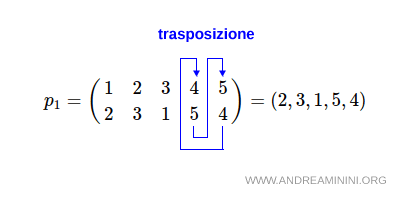
Ad esempio, il ciclo (1,2,3) posso scriverlo come prodotto di trasposizioni (1,2)(1,3). Il ciclo (4,5) è invece già una trasposizione.
Quindi la permutazione p1 posso riscriverla in questo modo
$$ p_1 = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \end{pmatrix} = (2,3,1,5,4) = (1,2,3)(4,5) = (1,2)(1,3)(4,5) $$
In base al numero delle trasposizioni la permutazione si dice
- Permutazione di classe pari
Se il numero delle trasposizioni è pari - Permutazione di classe dispari
Se il numero delle trasposizioni è dispari
In questo caso, la permutazione p1=(1,2)(1,3)(4,5) è composta da tre trasposizioni, quindi è una permutazione di classe dispari.
Come trovare tutte le permutazioni
Per trovare tutte le permutazioni di un insieme utilizzo il principio di enumerazione.
Metodo 1
Ho un insieme con 4 elementi
S = {1,2,3,4}
L'insieme ha complessivamente 4!=24 permutazioni
Divido 24 per il numero degli elementi n=4 e ottengo 24/4=6
Quindi scrivo 6 volte il primo elemento (1) dell'insieme
1
1
1
1
1
1
Restano da permutare n-1=3 elementi ossia 2,3,4
Ripartisco gli elementi restanti in questo modo
1,2
1,2
1,3
1,3
1,4
1,4
Scrivo il terzo elemento scrivendo un elemento mancante per ciascuna.
1,2,3
1,2,4
1,3,2
1,3,4
1,4,2
1,4,3
Nota. Nella scelta dell'elemento mancante seguo il criterio dell'ordinamento crescente. Ad esempio, alla tupla (1,2) mancano inizialmente gli elementi 3,4. Scelgo in ordine crescente prima tre (1,2,3) e poi quattro (1,2,4).
Infine, scrivo il quarto elemento delle tuple indicando l'ultimo elemento mancante per ciascuna
1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
A questo punto ripeto la stessa procedura scegliendo come primo elemento 2
2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1
2,4,1,3
2,4,3,1
Ripeto di nuovo la stessa procedura scegliendo come primo elemento 3
3,1,2,4
3,1,4,2
3,2,1,4
3,2,4,1
3,4,1,2
3,4,2,1
Ripeto nuovamente la stessa procedura scegliendo come primo elemento 4
4,1,2,3
4,1,3,2
4,2,1,3
4,2,3,1
4,3,1,2
4,3,2,1
Infine unisco i quattro gruppi in un'unica lista..
Ho così trovato tutte le 24 permutazioni dell'insieme {1,2,3,4}
1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1
2,4,1,3
2,4,3,1
3,1,2,4
3,1,4,2
3,2,1,4
3,2,4,1
3,4,1,2
3,4,2,1
4,1,2,3
4,1,3,2
4,2,1,3
4,2,3,1
4,3,1,2
4,3,2,1
Metodo 2
Ho un insieme con 4 elementi
S = {1,2,3,4}
L'insieme ha complessivamente 4!=24 permutazioni
Divido 24 per il numero degli elementi n=4 e ottengo 24/4=6
Quindi scrivo 6 volte il primo elemento (1) dell'insieme
1
1
1
1
1
1
Ora scrivo in verticale la sequenza 2,3,4 degli elementi mancanti
1,2
1,3
1,4
1,2
1,3
1,4
Slitto di un posto gli elementi nella sequenza da 2,3,4 a 3,4,2
Scrivo la sequenza 3,4,2 in verticale
1,2,3
1,3,4
1,4,2
1,2,3
1,3,4
1,4,2
Slitto di un posto gli elementi nella sequenza da 3,4,2 a 4,2,3
Scrivo la sequenza 4,2,3 in verticale
1,2,3,4
1,3,4,2
1,4,2,3
1,2,3,4
1,3,4,2
1,4,2,3
Nota. Gli elementi a partire dalla seconda colonna sono uguali in diagonale. E' una caratteristica utile che ne semplifica la scrittura. Una volta scritte le prime due colonne, le altre le ottengo meccanicamente.

Ripeto la stessa procedura ponendo l'elemento 2 al primo posto
2,1,3,4
2,3,4,1
2,4,1,3
2,1,3,4
2,3,4,1
2,4,1,3
Ripeto la stessa procedura ponendo l'elemento 3 al primo posto
3,1,2,4
3,2,4,1
3,4,1,2
3,1,2,4
3,2,4,1
3,4,1,2
Ripeto la stessa procedura ponendo l'elemento 4 al primo posto
4,1,2,3
4,2,3,1
4,3,1,2
4,1,2,3
4,2,3,1
4,3,1,2
Infine, unisco i quattro gruppi per ottenere l'elenco completo delle 24 permutazioni dell'insieme {1,2,3,4}
1,2,3,4
1,3,4,2
1,4,2,3
1,2,3,4
1,3,4,2
1,4,2,3
2,1,3,4
2,3,4,1
2,4,1,3
2,1,3,4
2,3,4,1
2,4,1,3
3,1,2,4
3,2,4,1
3,4,1,2
3,1,2,4
3,2,4,1
3,4,1,2
4,1,2,3
4,2,3,1
4,3,1,2
4,1,2,3
4,2,3,1
4,3,1,2
Il risultato finale è lo stesso.
E così via.
