Sistemi con ritardo finito
Un sistema con ritardo finito rispondono all'ingresso dopo un lasso di tempo. La risposta non è istantanea bensì ritardata.
Il modello matematico di un sistema con ritardo finito è rappresentabile con la seguente formula:
$$ F(s) = \frac{P(s)}{Q(s)} e^{-t_0s} $$
Dove e-t0s è la funzione di trasferimento di un ritardo finito pari a t0.
Nota. In alcuni software di simulazione non è possibile usare l'esponenziale e-t0s con la variabile indipendente s nell'esponente. Questo problema si può risolvere sostituendo l'esponenziale con un'approssimante di Padé.
Il ritardo modifica la stabilità del sistema
La presenza del ritardo modifica le condizioni di stabilità del sistema di controllo.
Pertanto, un modello retroazionato stabile con la risposta istantanea, potrebbe non esserlo più se la risposta è ritardata nel tempo.
Esempio. In questo diagramma di Nyquist è rappresentato un sistema senza ritardo (verde) e con un ritardo t0 (rosso).
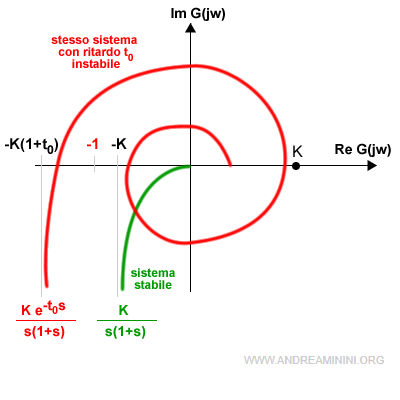
Secondo il criterio di Nyquist nel primo caso il sistema è stabile perché il diagramma (verde) non circonda il punto critico di Nyquist (-1) sull'asse reale. Nel secondo caso, invece, il diagramma (rosso) lo circonda e il sistema è instabile.
Il ritardo nei sistemi di tipo 0
Un sistema di tipo 0 non ha poli nell'origine
$$ \frac{K}{(1+τ_1s)(1+τ_2s)} $$
Il diagramma di Nyquist con K=1 è il seguente:
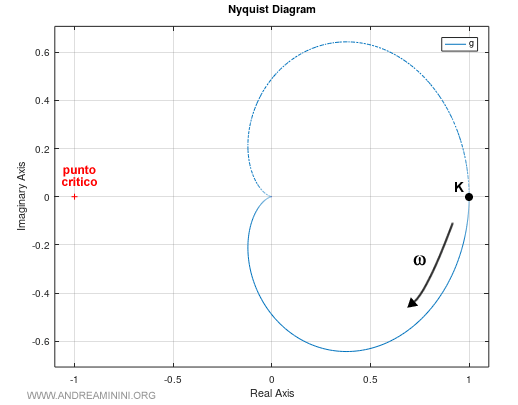
Introducendo un ritardo t0 diventa
$$ \frac{K \cdot e^{-t_0 s}}{(1+τ_1s)(1+τ_2s)} $$
Se il ritardo t0 è molto più grande dei coefficienti τ1 e τ2 ossia t0>>τ1,τ2 il diagramma di Nyquist diventa approssimativamente una circonferenza nel tratto iniziale (pur restando una spirale).
Pertanto, nell'asse reale negativo il diagramma passa all'incirca per il punto -K.
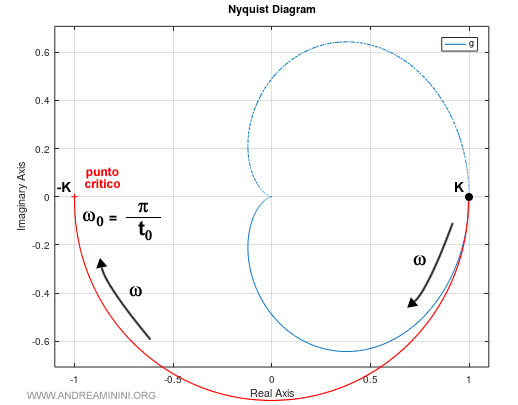
La pulsazione quando la fase è -180° (-π) è
$$ w_0 = \frac{π}{t_0} $$
Nota. Se il sistema ha origine nel punto K=1, il sistema con ritardo giunge al punto -K = -1 ossia al punto critico di Nyquist. Quando il diagramma di Nyquist circonda il punto -1 diventa instabile.
Se il sistema con ritardo oltrepassa il punto -1 sull'asse reale, il sistema diventa instabile.
Quindi, la condizione perché il sistema con ritardo finito sia asintoticamente stabile è K<1.
$$ K < 1 $$
Tuttavia, considerando il margine dell'errore a regime anche questa soluzione non è soddisfacente per garantire la stabilità asintotica
Come rendere stabile un sistema con ritardo finito
Per garantire la stabilità asintotica del sistema con ritardo finito è preferibile aggiungere un polo nell'origine, trasformando il sistema di tipo zero in un sistema di tipo uno.
$$ \frac{K \cdot e^{-t_0 s}}{s(1+τ_1s)(1+τ_2s)} $$
In questo modo la pulsazione quando la fase è -180° (-π) diventa
$$ w_0 = \frac{π}{2 \cdot t_0} $$
La presenza del polo all'origine riduce l'errore a regime e stabilizza il sistema retroazionato anche se ha un elevato ritardo finito.
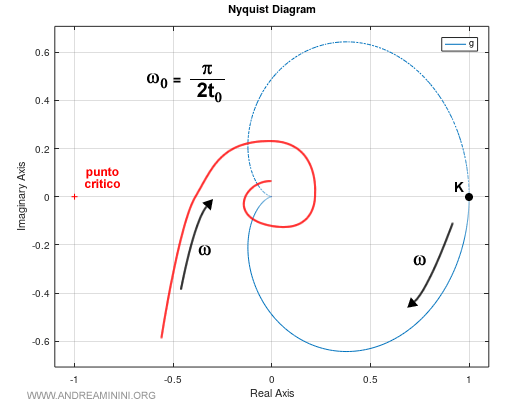
E così via.
