Un esempio di sistema di controllo

Questo esempio è un classico di sistema di controllo.

Ho un motore con una velocità angolare del rotore pari a ω. La tensione sull'armatura (v_a) mi permette di modificare la velocità ω.

$$ ω(t)= K \cdot Va $$

Devo fare in modo che la velocità del retore resti costante a ω'.

La costruzione del modello

In questo caso il motore è il sistema controllato.

• ω è la variabile controllata
• v_a è la variabile di controllo (manipolabile)
• v_r è il segnale di riferimento (set point) per mantenere costante la velocità a ω'.

Lo schema a blocchi è un semplice sistema a cascata.

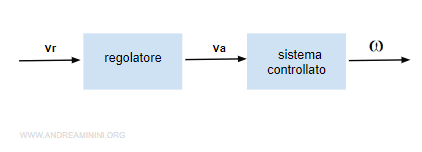
Si tratta di un sistema di controllo diretto perché la variabile di riferimento agisce direttamente sulla varabile di controllo, senza verificare l'effettiva velocità del rotore ω.

Criticità

Questo sistema ha evidenti criticità.

1. La presenza di errori e disturbi. La velocità ω è determinata dal voltaggio va ma anche da eventuali errori e disturbi. $$ ω_r = f(v_a, e) $$ Il segnale di riferimento v_r del sistema non considera l'uscita del sistema (ω). Quindi, non è in grado di compensare eventuali errori e disturbi che modificano la velocità del rotore (ω).
2. Il sistema funziona per i sistemi lineari. Non funziona se la relazione ingresso-uscita è non lineare ossia nei sistemi non lineari.

Soluzione

Per risolvere il problema mi basta aggiungere una retroazione per confrontare il valore calcolato ω con il valore reale di ω_r.

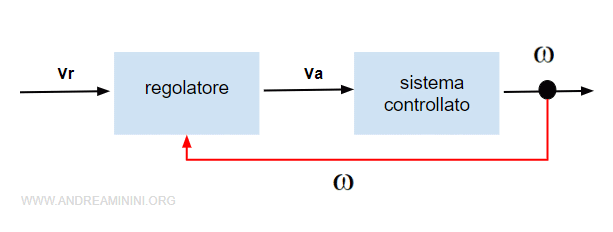
E' un esempio pratico di sistema con controllo a retroazione.

In questo modo se l'uscita del sistema controllato devia dal livello stimato, il regolatore può compensare il disturbo.

Nota. Quest'ultimo sistema integra sia il controllo diretto che il controllo a retroazione (rosso). E' un esempio pratico della complementarietà dei due metodi.

E così via.