Diagrammi di Nichols
Il diagramma di Nichols è uno strumento per rappresentare la funzione di risposta armonica G(jw). E' anche conosciuto come carta di Nichols.
Il piano di Nichols si costruisce sul diagramma cartesiano ponendo
- la fase (argomento) espressa in gradi sulle ascisse
- il modulo espresso in decibel sulle ordinate
Nota. Il diagramma di Nichols può essere tracciato su una carta semilogaritmica oppure su una carta ordinaria con ampiezza in decibel.
La rappresentazione di Nichols consiste in una sola curva graduata rispetto alla pulsazione ω.
E' quindi più sintetica rispetto al diagramma di Bode e simile ai diagrammi polari di Nyquist.
Nota. A differenza del diagramma di Nyquist, il diagramma di Nichols permette di comporre anche i diagrammi di più sistemi a cascata e analizzare meglio il comportamento del sistema per piccole variazioni nella pulsazione.
Una caratteristica del diagramma di Nichols è la sommabilità.
E' quindi possibile la costruzione di più sistemi in cascata sommando i componenti per uguali valori della pulsazione (ω).
In particolar modo, questa caratteristica consente di sommare il contributo delle singole funzioni elementari.
Come disegnare il diagramma di Nichols
Per disegnare il diagramma di Nichols sfrutto la sommabilità e analizzo le singole funzioni elementari della funzione di trasformazione in forma fattorizzata.
$$ G(s) = K \cdot \frac{ (1+τ'_1s) (1+τ'_2s) ... (1+2δ'_1 \frac{s}{ω'_{n1}} + \frac{s^2}{ω'^2_{n1}} ) (1+2δ'_2 \frac{s}{ω'_{n2}} + \frac{s^2}{ω'^2_{n2}} ) }{ s^h ( 1+τ_1s ) ( 1+τ_2s ) ... ( 1+2δ_1 \frac{s}{ω_{n1} } + \frac{s^2}{ω^2_{n1}} ) ( 1+2δ_2\frac{s}{ω_{n2}} + \frac{s^2}{ω^2_{n2}} ) } $$
Ecco l'analisi di ogni singola componente.
Guadagno
$$ G(jω)=K $$
Sul diagramma si disegna un punto corrispondente alla fase 0 p -π.
- Se la costante K è positiva la fase è zero.
- Se la costante K è negativa ka fase è -π
Monomio
$$ G(jω)=(jω)^-h $$
Si traccia una retta parallela all'asse delle ordinte in corrispondenza all'ascissa h(-π/2).
Binomio
$$ G(jω)=(1+jωτ)^{-1} $$
Per tracciare il binomio si utilizza la seguente curva che qui riporto in modo approssimativo
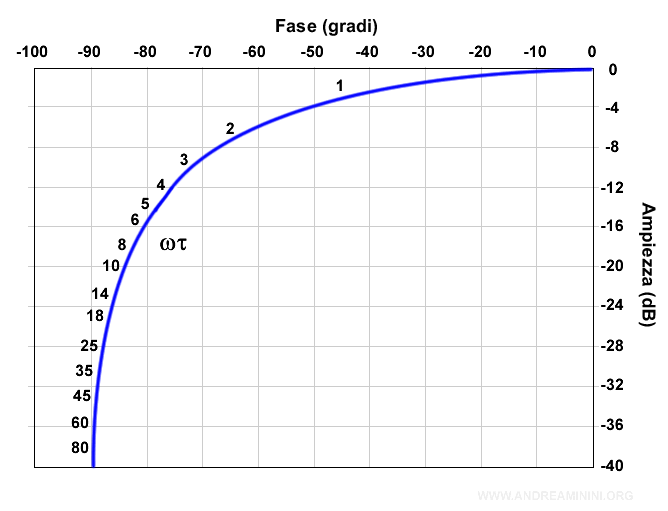
Per valori τ negativi il diagramma si ribalta sulle ordinate.
Nota. Nel caso del binomio al numeratore (1+jωτ) basta ribaltare il grafico intorno all'origine. Anche in questo caso, per τ<0 il diagramma si ribalta intorno all'asse delle ordinate.
Trinomio
$$ G(jω)=(1- \frac{ω^2}{ω^2_n} +j2δ \frac{ω}{ω_n} )^{-1} $$
Nel caso del trinomio la curva da considerare varia a seconda del valore δ dove 0≤δ≤1.
Anche in questo caso il grafico è approssimativo.
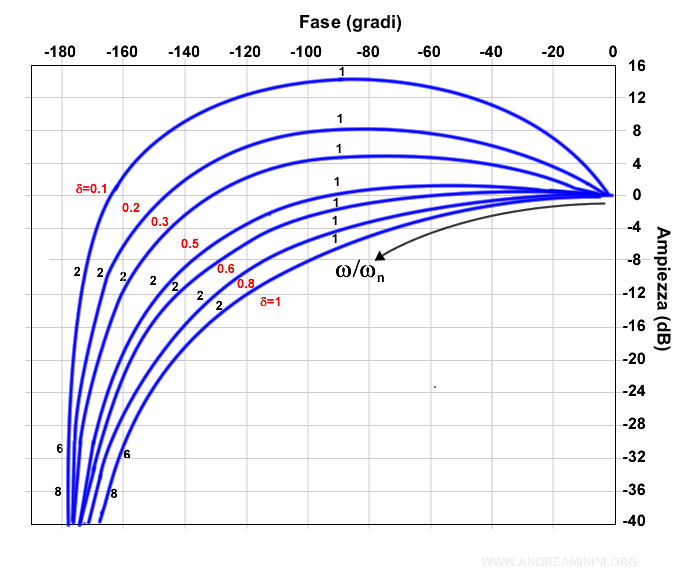
Per valori δ<0 il diagramma si ribalta intorno all'asse delle ordinate.
Nota. Il diagramma del trinomio al numeratore si ottiene ribaltando il grafico intorno all'origine. Per valori δ negativi si ribalta intorno all'asse delle ordinate.
E così via.
