Gli operatori lineari ortogonali

Un operatore lineare ortogonale ( o isometria ) è un operatore lineare che conserva il proprio prodotto scalare per ogni coppia di vettori v₁, v₂ dello spazio vettoriale reale V. $$ < f(v_1) , f(v_2) > = < v_1 , v_2 > $$

Cos'è un'isometria?

Un'isometria è una trasformazione geometrica, nel piano o nello spazio, che lascia invariate le lunghezze, gli angoli.

Quindi, in un'isometria le distanze tra due punti A e B sono costanti.

Nota. Nelle immagini dell'operatore lineare f i punti A e B conservano la stessa distanza.

Un esempio di operatore isometrico

Ho un operatore lineare f:V→V nello spazio vettoriale V=R² nel campo dei numeri reali ( K=R ).

Devo verificare se è un operatore isometrico.

$$ f = \begin{cases} x_1 \: cos \: θ - x_2 \: sin \:θ \\ x_1 \: sin \:θ + x_2 \: cos \:θ \end{cases} $$

La matrice di trasformazione A_f rispetto alla base canonica è la seguente:

$$ A_f = \begin{pmatrix} cos \: θ & - sin \: θ \\ sin \: θ & cos\: θ \end{pmatrix} $$

Ora prendo come riferimento due vettori v₁ e v₂ dello spazio vettoriale V

$$ v_1 = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \\ v_2 = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} $$

Poi calcolo le immagini di f(v₁) e f(v₂).

$$ f(v_1) = v_1 \cdot A_f = \begin{pmatrix} a_1 \: cos \: θ - a_2 \: sin \:θ \\ a_1 \: sin \:θ + a_2 \: cos \:θ \end{pmatrix} $$

$$ f(v_2) = v_2 \cdot A_f = \begin{pmatrix} b_1 \: cos \: θ - b_2 \: sin \:θ \\ b_1 \: sin \:θ + b_2 \: cos \:θ \end{pmatrix} $$

Per verificare se è un operatore lineare ortogonale, devo calcolare il prodotto scalare delle immagini

$$ < f(v_1) , f(v_2) > = < \begin{pmatrix} a_1 \: cos \: θ - a_2 \: sin \:θ \\ a_1 \: sin \:θ + a_2 \: cos \:θ \end{pmatrix} , \begin{pmatrix} b_1 \: cos \: θ - b_2 \: sin \:θ \\ b_1 \: sin \:θ + b_2 \: cos \:θ \end{pmatrix} > $$

$$ < f(v_1) , f(v_2) > = ( a_1 \: cos \: θ - a_2 \: sin \:θ ) \cdot ( b_1 \: cos \: θ - b_2 \: sin \:θ ) + \\ \:\:\:\:\:\:\:\:\:\:\:\: + ( a_1 \: sin \:θ + a_2 \: cos \:θ ) \cdot ( b_1 \: sin \:θ + b_2 \: cos \:θ ) $$

$$ < f(v_1) , f(v_2) > = a_1b_1 cos^2 \:θ - a_1b_2 cos \:θ sin \:θ - a_2b_1 sin \:θ cos \:θ + \\ \:\:\:\:\:\:\:\:\:\:\:\:+ a_2n_2 sin^2 \:θ + a_1b_1 sin^2 \:θ + a_1b_2 cos \:θ sin \:θ + a_2b_1 cos \:θ sin \:θ + a_2b_2 cos^2 \:θ $$

$$ < f(v_1) , f(v_2) > = a_1b_1 + a_2b_2 $$

$$< f(v_1) , f(v_2) > = < \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} , \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} > $$

$$< f(v_1) , f(v_2) > = < v_1 , v_2 > $$

Il prodotto scalare delle immagini <f(v₁),f(v₂)> è uguale al prodotto scalare dei vettori <v₁,v₂>.

Pertanto, l'operatore lineare f è ortogonale ossia è una isometria.

Le proprietà delle isometrie

Gli operatori lineari ortogonali hanno le seguenti proprietà:

• Un operatore lineare ortogonale è invertibile e la sua inversa f^-1 è uguale all'operatore aggiunto f*. $$ f^{-1}=f* $$

  Esempio
  
  La matrice A_f di un operatore lineare ortogonale rispetto alla base canonica è la seguente: $$ A_f = \begin{pmatrix} cos \: θ & - sin \: θ \\ sin \: θ & cos\: θ \end{pmatrix} $$ La matrice inversa A^-1 è uguale a $$ A_f^{-1} = \frac{1}{det(A_f)} \cdot cof(A_f)^T $$ $$ A_f^{-1} = \frac{1}{det(A_f)} \cdot ( cof ( \begin{pmatrix} cos \: θ & -sin \: θ \\ sin \: θ & cos \: θ \end{pmatrix} ) )^T $$ $$ A_f^{-1} = \frac{1}{det(A_f)} \cdot ( \begin{pmatrix} cos \: θ & -sin \: θ \\ sin \: θ & cos \: θ \end{pmatrix} )^T $$ $$ A_f^{-1} = \frac{1}{det(A_f)} \cdot \begin{pmatrix} cos \: θ & sin \: θ \\ -sin \: θ & cos \: θ \end{pmatrix} $$ Il determinante di A_f è uguale a 1 perché secondo la formula trigonometrica cos²+sin²=1. $$ A_f^{-1} = \begin{pmatrix} cos \: θ & sin \: θ \\ -sin \: θ & cos \: θ \end{pmatrix} $$
  Ora calcolo l'operatore lineare aggiunto f*. Secondo una proprietà delle applicazioni lineari aggiunte (f*), se la base è ortonormale (e la base canonica lo è) la matrice di un'applicazione aggiunta A_f* è uguale alla trasposta della matrice A_f.
  $$ A_f* = ( A_f )^T = ( \begin{pmatrix} cos \: θ & - sin \: θ \\ sin \: θ & cos\: θ \end{pmatrix} )^T = \begin{pmatrix} cos \: θ & sin \: θ \\ -sin \: θ & cos\: θ \end{pmatrix} $$
  Pertanto, la matrice inversa A^-1 è effettivamente uguale alla matrice trasposta di A_f ossia alla matrice della funzione aggiunta f*. $$ A_f^{-1} = A_{f*} $$ Se le matrici sono identiche (A_f^-1=A_f*) lo sono anche gli operatori lineari. $$ f^{-1} = f* $$

• Un operatore lineare ortogonale mantiene le stesse lunghezze sia nel dominio che nel codominio per ogni vettore dello spazio vettoriale reale V. $$ || f(v) || = ||v|| $$

  Dimostrazione
  
  La norma indotta dal prodotto scalare è la seguente

  

  Quindi, se sono uguali i prodotti scalari <f(v),f(v)>=<v,v>, lo sono anche le norme ||f(v)|| = ||v||.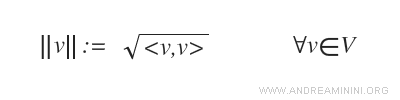
  
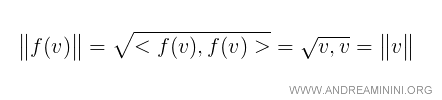
  E così via.