Come trasformare una base in ortogonale

Per trasformare una qualsiasi base vettoriale in una base vettoriale ortogonale, è sufficiente proiettare il vettore sull'altro vettore non nullo tramite i coefficienti di Fourier.

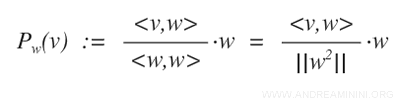
Dove il coefficiente di Fourier è il rapporto

$$ \frac{<v,w>} {<w,w>} $$

I coefficienti di Fourier sono alla base del metodo di ortogonalizzazione di Gram-Schmidt.

A partire dalla proiezione P_w(v) si può costruire una base ortogonale a partire da una base qualunque con la seguente formula:

$$ w_1 = v_1 $$ $$ w_i = v_i - \sum_{ j=1}^{i-1} P_wj(v_i) \:\:\:\: per \:\:\:\: i=2,...n $$

Ovviamente, la base ortogonale così ottenuta non è l'unica possibile, perché dipende dall'ordine dei vettori nella base.

Nota. La base ortogonale ottenuta ha alcune proprietà definite dall'ortogonalizzazione di Gram-Schmidt. Ad esempio, è un generatore dello stesso spazio vettoriale. Se i vettori della base iniziale sono linearmente indipendenti, allora dopo la trasformazione anche i vettori della base ortogonale sono indipendenti.

Una volta ottenua la base ortogonale, si può infine trasformare la base ortogonale in ortonormale.

I coefficienti di Fourier

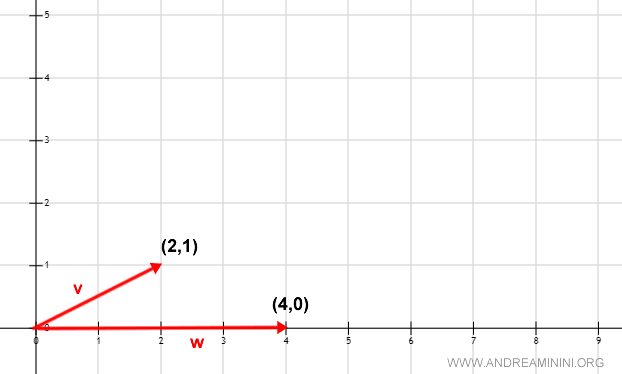
In uno spazio vettoriale V=R² su K=R ho una base vettoriale B composta dai seguenti vettori:

$$ B = \{ v , w \} = \{ ( 2,1 ) , ( 4,0 ) \} $$

Non è una base ortogonale, perché il prodotto scalare <v,w> è uguale a 8.

$$ <v,w> = (2*4)+(1*0) = 8 $$

Osservando la rappresentazione grafica sul piano è evidente la non ortogonalità ( non perpendicolarità ) dei vettori.

Il prodotto scalare induce la norma ||·||

Per trasformarla in una base ortogonale, considero la proiezione ortogonale P_w(v) del vettore v su w.

$$ P_w(v) = (2,0 ) $$

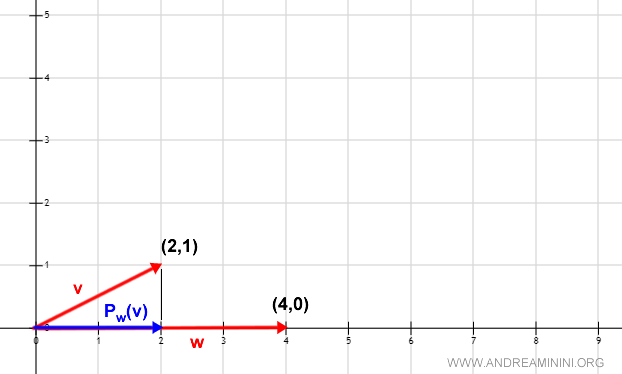
Il vettore P_w(v) è un multiplo del vettore w, ossia esiste uno scalare k di R tale che

$$ k*P_w(v)=w $$

Nota. In questo semplice esempio lo scalare è evidente, moltiplicando P_w(v) per 2 si ottiene il vettore w.

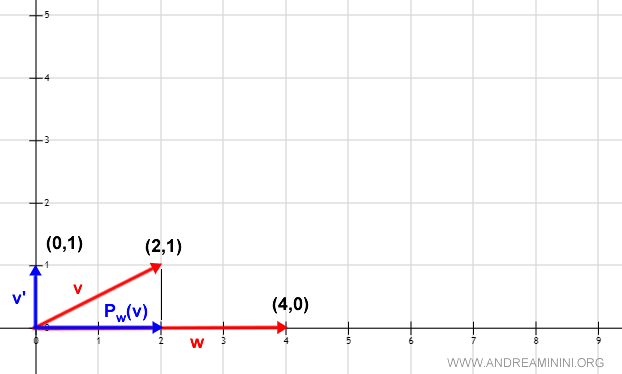
Poi calcolo la differenza tra il vettore v e la proiezione ortogonale P_w(v)

$$ v' = v - P_w \\ v' = (2,1) - (2,0) \\ v' = (0,1) $$

Grazie alla differenza ottengo un vettore ortogonale a P_w(v).

Lo indico per semplicità con il simbolo v'.

Basta un'analisi grafica per appurare l'ortogonalità tra v' e la proiezione P_w(v).

Essendo v' un vettore ortogonale a w, il prodotto scalare <v',P_w(v)> è nullo.

 

$$ <v',P_w(v)> = 0 $$

Sostituisco v' con v-P_w(v) ottengo

 

$$ <v',P_w(v)> = 0 \\ <v-P_w(v),P_w(v)> = 0 $$

Per la terza proprietà del prodotto scalare: $$ <a+b, c> = <a,c>+<b,c> $$

Riscrivo l'equazione nel seguente modo:

$$ <v,P_w(v)> - <P_w(v),P_w(v)> = 0 $$

Sapendo che P_w(v) è un multiplo di w

$$ P_w(v) = k \cdot w $$

posso sostituire P_w(v) con kw

$$ <v,kw> - <kw,kw> = 0 \\ <v,kw> - k<w,w> = 0 $$

Per la quarta proprietà del prodotto scalare: $$ <ka,b> = k<a,b>$$

Pertanto, posso trasformare l'equazione nel seguente modo:

$$ k \cdot <v,w> - k<w,w> = 0 $$

A parte il caso del vettore (k=0) escluso a priori, questa equazione è soddisfatta quando lo scalare k assume il seguente valore:

$$ k = \frac{<v,w>}{<w,w>} $$

Lo scalare è detto coefficiente di Fourier del vettore v rispetto a w.

Quindi, la proiezione ortogonale del vettore v sul vettore w è uguale a

$$ P_w(v) := \frac{<v,w>}{<w,w>} \cdot w = \frac{<v,w>}{||w^2||} \cdot w $$

Tornando all'esempio precedente, il coefficiente di Fourier

$$ k = \frac{<v,w>}{<w,w>} = \frac{ 8 }{ 16 } = \frac{ 1 }{ 2 } $$

la proiezione ortogonale del vettore v su w è:

$$ P_w(v) = \frac{<v,w>}{<w,w>} \cdot w = \frac{1}{2} \cdot (4,0) = (2,0) $$

E così via.

Ortogonalizzazione di Gram-Schmidt

Il metodo di ortogonalizzazione di Gram-Schmidt mi permette di usare i coefficienti di Fourier per trasformare qualsiasi base vettoriale in una base ortogonale.

Dato un generatore L di n vettori {v_i}nello spazio vettoriale V nel campo K=R, esiste sempre un generatore L' di n vettori ortogonali tra loro {w_i} uguale a L. $$ L\{v_1,...,v_n\} = L'\{w_1,...,w_n\} \\ <w_i,w_j>=0 \:\: con \:\: i \ne j $$

Se i vettori del generatore iniziale L erano linearmente indipendenti, allora anche quelli ortogonali del generatore L' sono linearmente indipendenti.

Quindi, se il generatore L è una base, allora anche il generatore L' è una base.

La formula per trovare i vettori ortogonali della base

Per trovare i vettori ortogonali il metodo utilizza la seguente formula:

Il primo vettore v1 del generatore L resta lo stesso (w1=v1) anche nel generatore L'. $$ w_1 = v_1 $$ I vettori successivi, invece, sono ortogonalizzati tramite la proiezione ortogonale e il coefficiente di Fourier. $$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: per \:\:\:\: i=2,...n $$

Il risultato finale è una base ortogonale dello spazio vettoriale V.

Nota. Ovviamente, la base non è l'unica possibile perché dipende anche dalla posizione dei vettori nella base iniziale.

Un esempio pratico

Nello spazio vettoriale V=R³ nel campo K=R ho la seguente base:

$$ B = \{ v_1 , v_2, v_3 \} = \{ ( 1,1,1 ) , ( -1,1,0 ) , ( 1,2,1 ) \} $$

E' composta da tre vettori lineramente indipendenti.

Non sono vettori ortogonali poiché il prodotto scalare tra loro è diverso da zero e la norma è diversa da 1.

I prodotti scalari tra i vettori <v₁,v₂> , <v₁,v₃> e <v₂,v₃> della base sono i seguenti:

$$ < v_1 , v_2 > = 1 \cdot -1 + 1 \cdot 1 + 1 \cdot 0 = 0 \\ < v_1 , v_3 > = 1 \cdot 1 + 1 \cdot 2 + 1 \cdot 1 = 4 \\ < v_2 , v_3 > = -1 \cdot 1 + 1 \cdot 2 + 0 \cdot 1 = 1 $$

Per calcolare la base ortogonale B' seguo il metodo di Gram-Schmidt.

$$ B' = \{ w_1 ,w_2,w_3 \} $$

Il primo vettore della base ortogonale è uguale al primo vettore della base di partenza.

$$ w_1 = v_1 = (1,1,1) $$

Il secondo vettore della base ortogonale è invece determinato dalla formula di Gram-Schmidt.

$$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: per \:\:\:\: i=2,...n $$

$$ w_2 = v_2 - \sum_{ j=1}^{2-1} P_{wj}(v_2) \:\:\:\: per \:\:\:\: i=2,...n $$

$$ w_2 = v_2 - P_{w1}(v_2) $$

La proiezione ortogonale P_w del vettore v₂ è la seguente:

$$ P_{w1}(v_2) = \frac{<v_2,w_1>} {<w_1,w_1>} \cdot w_1 $$

$$ P_{w1}(v_2) = \frac{< ( -1,1,0 ) , (1,1,1) >} {< (1,1,1) , (1,1,1) >} \cdot (1,1,1) $$

$$ P_{w1}(v_2) = \frac{ -1 \cdot 1 + 1 \cdot 1 + 0 \cdot 0 } { 1^2 + 1^2 + 1^2 } \cdot (1,1,1) $$

$$ P_{w1}(v_2) = \frac{ 0 } { 3 } \cdot (1,1,1) $$

$$ P_{w1}(v_2) = 0 $$

Quindi, tornando alla formula di Gram-Schmidt, posso determinare il secondo vettore w₂ della base ortogonale B'.

$$ w_2 = v_2 - P_{w1}(v_2) $$

$$ w_2 = ( -1,1,0 ) - 0 $$

$$ w_2 = ( -1,1,0 ) $$

A questo punto posso calcolare il terzo e ultimo vettore w₃ della base ortogonale sempre tramite formula di Gram-Schmidt.

$$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: per \:\:\:\: i=2,...n \\ w_3 = v_3 - \sum_{ j=1}^{3-1} P_{wj}(v_3) \:\:\:\: per \:\:\:\: i=2,...n \\ w_3 = v_3 - P_{w1}(v_3) - P_{w2}(v_3) $$

La proiezione ortogonale P_w1 del vettore v₃ è la seguente:

$$ P_{w1}(v_3) = \frac{<v_3,w_1>} {<w_1,w_1>} \cdot w_1 $$

$$ P_{w1}(v_3) = \frac{<(1,2,1),(1,1,1)>} {<(1,1,1),(1,1,1)>} \cdot (1,1,1) $$

$$ P_{w1}(v_3) = \frac{ 1 \cdot 1 + 2 \cdot 1 + 1 \cdot 1 } { 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 } \cdot (1,1,1) $$

$$ P_{w1}(v_3) = \frac{ 4 } { 3 } \cdot (1,1,1) $$

$$ P_{w1}(v_3) = ( \frac{ 4 } { 3 } \cdot 1 , \frac{ 4 } { 3 } \cdot 1 , \frac{ 4 } { 3 } \cdot 1 ) $$

$$ P_{w1}(v_3) = ( \frac{ 4 } { 3 } , \frac{ 4 } { 3 } , \frac{ 4 } { 3 } ) $$

La proiezione ortogonale P_w2 del vettore v₃ è la seguente:

$$ P_{w2}(v_3) = \frac{<v_3,w_2>} {<w_2,w_2>} \cdot w_2 $$

$$ P_{w2}(v_3) = \frac{<(1,2,1),( -1,1,0 )>} {<( -1,1,0 ),( -1,1,0 )>} \cdot ( -1,1,0 ) $$

$$ P_{w2}(v_3) = \frac{1 \cdot -1 + 2 \cdot 1 + 1 \cdot 0 } { -1 \cdot -1 + 1 \cdot 1 + 0 \cdot 0 } \cdot ( -1,1,0 ) $$

$$ P_{w2}(v_3) = \frac{ 1 } { 2 } \cdot ( -1,1,0 ) $$

$$ P_{w2}(v_3) = ( -1 \cdot \frac{ 1 } { 2 },1 \cdot \frac{ 1 } { 2 },0 \cdot \frac{ 1 } { 2 } ) $$

$$ P_{w2}(v_3) = ( - \frac{ 1 } { 2 }, \frac{ 1 } { 2 }, 0 ) $$

A questo punto posso calcolare il terzo e ultimo vettore w₃ della base ortogonale sempre tramite formula di Gram-Schmidt.

$$ w_3 = v_3 - P_{w1}(v_3) - P_{w2}(v_3) \\ w_3 = (1,2,1) - ( \frac{ 4 } { 3 } , \frac{ 4 } { 3 } , \frac{ 4 } { 3 } ) - ( - \frac{ 1 } { 2 }, \frac{ 1 } { 2 }, 0 ) \\ w_3 = (1 - \frac{ 4 } { 3 } + \frac{ 1 } { 2 } ,2 - \frac{ 4 } { 3 } - \frac{ 1 } { 2 } , 1 - \frac{ 4 } { 3 } - 0 ) \\ w_3 = ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) \\ w_3 = ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) $$

In conclusione, i vettori della base ortogonale B' sono i seguenti:

$$ B' = \{ w_1, w_2, w_3 \} $$ $$ B' = \{ (1,1,1), (-1,1,0) , ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) \} $$

Ho così trovato una base ortogonale equivalente.

Nota. E' soltanto una base ortogonale tra quelle possibili. Se invertissi l'ordine dei vettori della base B, otterrei una base ortogonale B' diversa.

Verifica

Per sicurezza verifico se i vettori w₁, w₂, w₃ sono effettivamente ortogonali tra loro calcolando i loro prodotti scalari.

$$ < w_1 ,w_2 > = 1 \cdot -1 + 1 \cdot 1 + 1 \cdot 0 = 0 \\ < w_1 , w_3 > = 1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ -1 } { 3 } = 0 \\ < w_2 ,w_3 > = -1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ 1 } { 6 } + 0 \cdot \frac{ 1 } { 6 } = 0 $$

I prodotti scalari sono tutti uguali a zero, ciò conferma che i vettori w₁, w₂, w₃ sono ortogonali tra loro.

I vettori w₁, w₂, w₃ sono anche ortonormali?

No, i vettori non sono ortonormali perché la norma dei vettori è diversa da 1.

$$ || w_1 || = \sqrt{ 1^2+1^2+1^2 } = \sqrt{3} \\ || w_2 || = \sqrt{ -1^2+1^2+0^2 } = \sqrt{ 2 } \\ || w_3 || = \sqrt{ ( \frac{ 1 } { 6 }) ^2+( \frac{ 1 } { 6 })^2+(- \frac{ 1 } { 3 })^2 }= \sqrt{ \frac{ 1 } { 6 } } $$

E' comunque possibile trasformare la base ortogonale in ortonormale, normalizzando i tre vettori.

In quest'altro esempio si può vedere la procedura di trasformazione di una base ortogonale in ortonormale.