Come verificare se tre punti sono allineati
Per capire se tre punti sono allineati oppure no, calcolo l'equazione della retta passante tra due dei tre punti. Poi verifico se il terzo punto appartiene o meno alla retta.
Posso usare sia le equazioni parametriche che cartesiane della retta.
E' comunque più facile usare le equazioni cartesiane.
Nota. Usando le equazioni cartesiane mi basta sostituire le coordinate di un punto nell'equazione e verificare se è soddisfatta. Con le equazioni parametriche, invece, devo risolvere un sistema di equazioni. E' quindi un procedimento più lungo e complesso.
Esempio con le equazioni parametriche
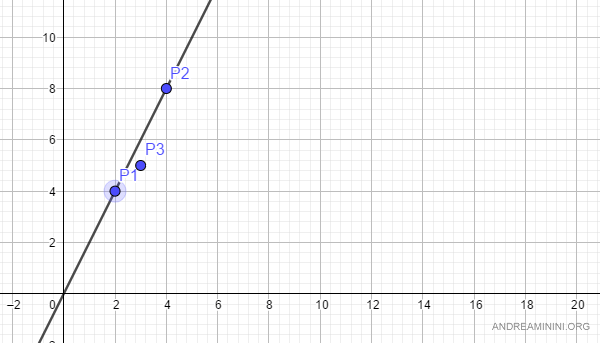
Dati tre punti P1,P2,P3 sul piano cartesiano, devo verificare se sono allineati oppure no.
$$ P_1 = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ P_2 = \begin{pmatrix} 4 \\ 8 \end{pmatrix} $$
$$ P_3 = \begin{pmatrix} 3 \\ 5 \end{pmatrix} $$
Prendo due punti, ad esempio P1 e P2, e calcolo la retta passante per i due punti.
Fisso un verso arbitrario da P2 a P2.
L'equazione vettoriale della retta è la seguente:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$
Dove l'ultima componente è il vettore direttore.
Il punto d'origine del vettore e di destinazione del vettore sono:
$$ P_1 = \begin{pmatrix} x_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 4 \\ 8 \end{pmatrix} $$
Quindi l'equazione vettoriale diventa
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 4 - 2 \\ 8 - 4 \end{pmatrix} $$
Ottengo così le equazioni parametriche della retta.
$$ \begin{cases} x = 2 + 2 t \\ y = 4 + 4 t \end{cases} $$
A questo punto, verifico se il terzo punto appartiene alla retta oppure no.
Nota. Se P3 appartiene alla retta, allora P1, P2 e P3 sono allineati. Viceversa, se P3 non appartiene alla retta, i tre punti non sono allineati.
Sostituisco le coordinate di P3 (3,5) nelle equazioni parametriche
$$ \begin{cases} 3 = 2 + 2 t \\ 5 = 4 + 4 t \end{cases} $$
$$ \begin{cases} t = \frac{1}{2} \\ 5 = 4 + 4 ( \frac{1}{2} ) \end{cases} $$
$$ \begin{cases} t = \frac{1}{2} \\ 5 = 6 \end{cases} $$
Il sistema non soluzioni.
Pertanto, il punto P3 non appartiene alla retta e i punti P1,P2, P3 non sono allineati.
E così via.
Esempio con l'equazione cartesiana
Un metodo alternativo per verificare se tre punti sono allineati è tramite l'equazione cartesiana.
Dati tre punti P1, P2, P3
$$ P_1 = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ P_2 = \begin{pmatrix} 4 \\ 8 \end{pmatrix} $$
$$ P_3 = \begin{pmatrix} 3 \\ 5 \end{pmatrix} $$
Per prima cosa devo calcolare l'equazione cartesiana della retta che passa due dei tre punti.
Ad esempio, la retta passante per P1 e P2.
$$ P_2 P_1 = \begin{pmatrix} 4-2 \\ 8-4 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Il vettore P2P1 è il vettore direttore della retta.
Quindi l'equazione vettoriale della retta è la seguente:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Scelgo il punto P1 come punto qualsiasi P0 della retta.
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + t \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} - \begin{pmatrix} 2 \\ 4 \end{pmatrix} = t \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ \begin{pmatrix} x - 2 \\ y - 4 \end{pmatrix} = t \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Calcolo il determinante dei vettori in colonna mettendo a zero il risultato.
$$ det \begin{pmatrix} x - 2 & 2 \\ y - 4 & 4 \end{pmatrix} = (x-2)4 -2(y-4) = 0 $$
Nota. Ho posto a zero il determinante perché il rango della matrice deve essere inferiore a due. So già che i due vettori sono linearmente dipendenti perché sono vettori proporzionali. Quindi, se i vettori sono linearmente dipendenti, il determinane dei vettori deve essere uguale a zero.
Ottengo così l'equazione cartesiana della retta.
$$ 4x -2y = 0 $$
A questo punto per capire se il terzo punto è allineato, devo solo verificare se il punto appartiene alla retta.
Sostituisco le coordinate del punto P3 (3,5) nell'equazione cartesiana e verifico se è soddisfatta.
$$ 4(3) -2(5) = 0 $$
$$ 12 - 10 = 0 $$
$$ 2 = 0 $$
L'equazione non è soddisfatta.
Pertanto, il punto P3 non appartiene alla retta.
Se il punto P3 non appartiene alla retta P2P1 non può essere allineato con i punti P1 e P2.
E così via.
