Come verificare se un punto appartiene alla retta

Per verificare se un punto P appartiene a una retta posso usare le equazioni cartesiane o parametriche della retta.

E' comunque preferibile usare le equazioni cartesiane

Nota. La verifica con l'equazione cartesiana della retta è più facile e rapida. Devo solo sostituire le coordinate del punto nell'equazione e vedere se l'equazione è soddisfatta. La verifica con le equazioni parametriche è invece più lunga e complessa perché devo risolvere il sistema di equazioni.

Esempio con l'equazione cartesiana

Ho una retta passante per i punti P₁ e P₂.

$$ P_1 = \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ P_2 = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

La rappresentazione grafica sul diagramma cartesiano è la seguente:

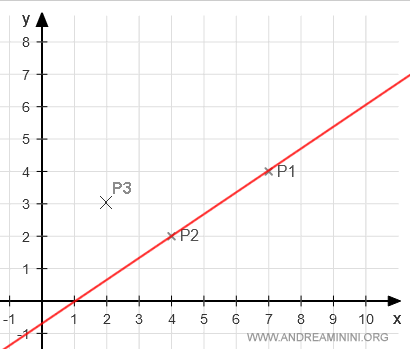
L'equazione cartesiana della retta è la seguente:

$$ -2x + 3y +2 = 0 $$

Caso 1

Voglio verificare se il punto P₃ (2,3) appartiene alla retta.

$$ P_3 \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Sostituisco le coordinate del punto P₃ alle variabili x e y dell'equazione cartesiana.

$$ -2(2) + 3(3) +2 = 0 $$

$$ -4 + 9 +2 = 0 $$

$$ 7 = 0 $$

L'equazione non è soddisfatta.

Il punto P₃ con coordinate (2,3) non appartiene alla retta.

Caso 2

Ora voglio verificare se il punto P₂ (4,2) appartiene alla retta.

$$ P \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Sostituisco le coordinate del punto P₂ alle variabili x e y dell'equazione.

$$ -2(4) + 3(2) +2 = 0 $$

$$ -8 + 6 +2 = 0 $$

$$ 0 = 0 $$

L'equazione è soddisfatta il punto P₂ (4,2) appartiene alla retta.

E così via.

Esempio con l'equazione parametrica

Ho una retta passante per i punti P₁ e P₂.

$$ P_1 = \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ P_2 = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

La rappresentazione grafica sul diagramma cartesiano è la seguente:

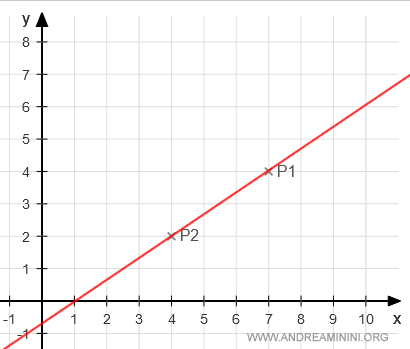
I due punti determinano il vettore P₁P₂

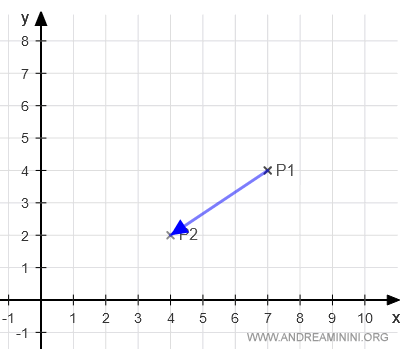
Nota. In questo caso ho fissato arbitrariamente un verso da P₁ a P₂. Avrei potuto scegliere anche il contrario, ossia da P₂ a P₁, ottenendo però equazioni diverse.

L'equazione vettoriale della retta è la seguente:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 4 - 7 \\ 2 -4 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

Posso così ottenere le equazioni parametriche

$$ \begin{cases} x = 7 - 3t \\ y = 4 - 2t \end{cases} $$

Il punto P appartiene alla retta?

Voglio verificare se il punto P(2,3) appartiene alla retta.

Sostituisco le coordinate del punto P alle variabili x e y dell'equazione parametrica.

$$ \begin{cases} 2 = 7 - 3t \\ 3 = 4 - 2t \end{cases} $$

Se il sistema ha una soluzione, allora il punto appartiene alla retta.

Viceversa, il punto non appartiene alla retta.

In questo caso, il sistema non ha soluzione perché il punto P non si trova sulla retta.

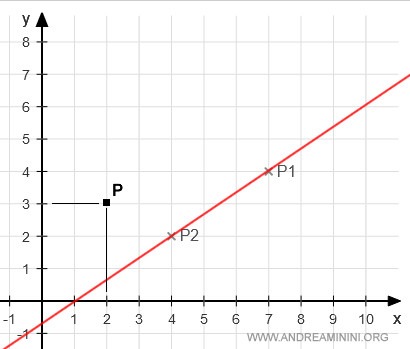
Verifica $$ \begin{cases} 2 = 7 - 3t \\ (4-3)/2 = t \end{cases} $$ $$ \begin{cases} 2 = 7 - 3(4-3)/2 \\ (4-3)/2 = t \end{cases} $$ $$ \begin{cases} 2 = 7 - 3(1/2) \\ t=1/2 \end{cases} $$ $$ \begin{cases} 7 - 2 - 3(1/2) = 0 \\ t=1/2 \end{cases} $$ $$ \begin{cases} 5 - 3(1/2) = 0 \\ t=1/2 \end{cases} $$ $$ \begin{cases} 3.5 = 0 \\ t=1/2 \end{cases} $$

Metodo alternativo

Posso verificare la relazione di appartenenza alla retta anche senza calcolare il sistema.

E' sufficiente trasformare le equazioni parametriche in un'equazione cartesiana.

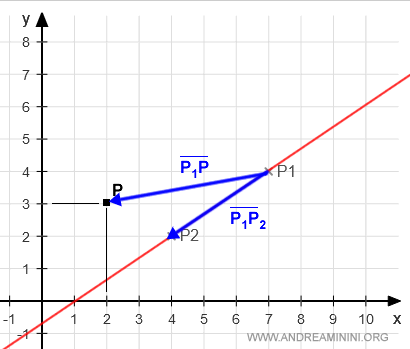
$$ \overrightarrow{P_1P} = \begin{pmatrix} x \\ y \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} = \begin{pmatrix} x-7 \\ y-4 \end{pmatrix} $$

$$ \overrightarrow{P_1P_2} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

I due vettori sono tracciati entrambi a partire dal punto iniziale P₁ verso il punto P e verso il punto P₂.

Se il punto P si trova sulla stessa retta del vettore P₁P₂ i due vettori sono vettori proporzionali.

Se i due vettori sono vettori proporzionali allora sono anche vettori linearmente dipendenti.

In questo caso, il determinante della matrice composta dai due vettori è uguale a zero.

$$ det \begin{pmatrix} x-7 & -3 \\ y-4 & -2 \end{pmatrix} = 0 $$

Nota. Sostituendo alle variabili x e y le coordinate del punto P(2,3) posso già verificare se i vettori sono proporzionali. Se sono linearmente dipendenti il determinante è nullo. $$ det \begin{pmatrix} (2)-7 & -3 \\ (3)-4 & -2 \end{pmatrix} = 10 - 3 = 7 ≠ 0. $$ Il determinante è diverso da zero. Pertanto, il punto P non si trova sulla retta perché i due vettori non sono linearmente dipendenti. Se non sono linearmente dipendenti, non sono nemmeno vettori proporzionali.

Svolgo i calcoli del determinante e ottengo l'equazione cartesiana della retta.

$$ (x-7) (-2) - (-3) (y-4) = 0 $$

$$ -2x + 14 + 3y - 12 = 0 $$

$$ -2x + 3y + 2 = 0 $$

A questo punto, basta sostituire le coordinate del punto P ( 2,3 ) e verificare se l'equazione è soddisfatta.

$$ -2(2) + 3(3) + 2 = 0 $$

$$ -4 + 9 + 2 = 0 $$

$$ 7 = 0 $$

L'equazione non è soddisfatta.

Pertanto, il punto P non appartiene alla retta.