Numeri primi
Cosa sono i numeri primi
Un numero primo è un numero intero maggiore di 1 divisibile per 1 e per se stesso.
In altre parole, un numero primo ha soli due divisori distinti: 1 e se stesso.
Sono numeri primi i seguenti numeri
$$ 2 \ , \ 3 \ , \ 5 \ , \ 7 \ , \ 11 \ , \ 13 \ , \ 17 \ , \ 19 \ , \ 23 \ , \ 29 \ , \ 31 \ ... $$
Ad esempio, il numero 7 ha due divisori distinti, il numero 1 e il numero 7.
$$ 7:1 = 7 $$
$$ 7:7 = 1 $$
Non ci sono altri divisori, pertanto il numero 7 è un numero primo.
Il numero 1 non è un numero primo perché è divisibile solo per un numero, ossia per 1. Inoltre, se il numero 1 fosse considerato un numero primo, i numeri non avrebbero più una fattorizzazione unica, contraddicendo al teorema fondamentale dell'aritmetica.
Una definizione alternativa
In alternativa, un numero primo può essere definito anche in questo modo:
Un intero a è detto numero primo se ogni volta che divide un prodotto bc, dove b e c sono interi, allora divide almeno uno dei due fattori. $$ \forall a|bc \rightarrow a|b ∨ a|c$$
Ad esempio, considero il numero primo \( a = 3 \), e verifico la proprietà con un prodotto \( bc \).
Scelgo \( b = 6 \) e \( c = 5 \), quindi \( bc = 6 \times 5 = 30 \).
In questo caso, \( a= 3 \) divide il prodotto \( bc=30 \) e divide anche almeno uno dei fattori \( b = 6 \), confermando la definizione.
Quanti sono i numeri primi? I numeri primi sono infiniti. E' stato dimostrato per la prima volta da Euclide. Il numero primo più grande finora conosciuto è il numero 282 589 933−1, è stato trovato nel 2018 ed è composto da oltre 24 milioni di cifre decimali.[
Un metodo per trovare i numeri primi da 2 a N è il crivello di Eratostene.
La scomposizione in fattori primi
Ogni numero intero non primo può essere scomposto in un prodotto di numeri primi.
Esempio
Il numero 30 non è un numero primo.
La scomposizione in numeri primi di 30 è
$$ 30 = 2 \cdot 3 \cdot 5 $$
Il numero 30 è divisibile per 2, per 3 e per 5, oltre che per 1 e per se stesso.
Quindi, non è un numero primo.
Il teorema fondamentale dell'aritmetica
Secondo il teorema fondamentale dell'aritmetica:
Qualsiasi numero intero diverso da 1 può essere fattorializzato nel prodotto di n elementi irriducibili distinti tra loro con esponente positivo e_k>0 e la fattorizzazione è unica. $$ n=f_1^{e_1} \cdot f_2^{e_2} ... f_k^{e_k} $$
Ad esempio, prendo il numero intero \( n = 180 \).
Scompongo il numero in fattori primi.
$$ 180 = 2^2 \cdot 3^2 \cdot 5^1 $$
In questo caso, 2, 3 e 5 sono numeri primi (irriducibili) e gli esponenti \( e_1 = 2 \), \( e_2 = 2 \) e \( e_3 = 1 \) sono positivi.
Secondo la fattorizzazione, posso esprimere \( n = 180 \) come:
$$ n = f_1^{e_1} \cdot f_2^{e_2} \cdot f_3^{e_3} = 2^2 \cdot 3^2 \cdot 5^1 $$
La fattorizzazione è unica a meno dell'ordine dei fattori.
$$ 180 = 2^2 \cdot 3^2 \cdot 5^1 $$
Questo rispetta il teorema fondamentale dell'aritmetica.
Lo stesso vale per qualsiasi altro numero n maggiore di uno.
Nota. Se cambiassi l'ordine dei fattori, la fattorizzazione resterebbe comunque unica, poiché i fattori primi sono sempre gli stessi. $$ 180 = 2^2 \cdot 3^2 \cdot 5^1 = 3^2 \cdot 5^1 \cdot 2^2 = 5^1 \cdot 2^2 \cdot 3^2 $$
Teorema dei numeri primi
Il limite del rapporto p(x)/(x/log x ) tende a 1. $$ \lim_{x \rightarrow ∞} \frac{p(x)}{\frac{x}{log \:x}} = 1 $$ dove x è un numero reale x>0 e p(x) è la quantità di numeri primi inferiori di x.
Quindi, la probabilità che un numero intero n sia un numero primi è pari a 1/log n.
Fu Gauss ad accorgersi che la serie dei numeri primi ha lo stesso andamento asintotico della funzione x/log x.
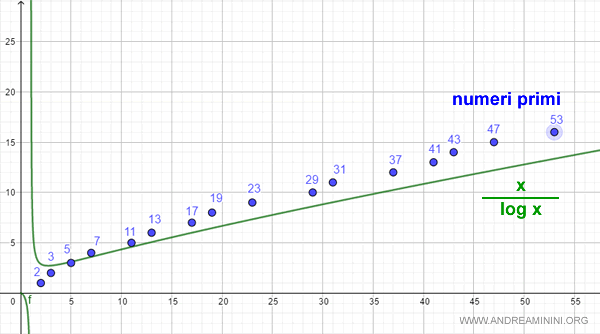
Quindi, la funzione x/log x mi permette di stimare quanti numeri primi precedono un numero n.
Esempio. Voglio sapere quanti primi precedono il numero n=55 tramite la formula di Gauss. $$ \frac{n}{\log n} = \frac{55}{\log 55} = 13.72 $$ Secondo la formula ci sono circa 14 numeri primi inferiori di n=55. In realtà, contandoli ce ne sono 16 di numeri primi inferiori a 55 ma la formula si è comunque avvicinata molto al risultato e diventa particolarmente utile per numeri n interi molto grandi.
Pertanto, la probabilità che un numero n sia un numero primo è
$$ \frac{1}{\log n} $$
Quindi, con log n tentativi dovrei trovare un primo superiore di n.
$$ \log n $$
Esempio. Voglio trovare il numero primo successivo al numero n=43. $$ \log 43=3.76 $$ Secondo la stima, dovrei compiere circa 4 tentativi. $$ 44 \text{ tentativo 1 } \\ 45 \text{ tentativo 2 } \\ 46 \text{ tentativo 3 } \\ 47 \text{ numero primo - tentativo 4 } $$ Ho trovato il numero primo successivo di 43 con 4 tentativi. La formula è soltanto una stima, non è precisa ma si avvicina realisticamente al numero dei tentativi da provare. E' molto utile nella crittografia.
I numeri primi di Mersenne
I numeri di Mersenne sono numeri interi della forma:
$$ M_n = 2^n - 1 $$
Dove \( n \) è un numero intero positivo.
Non tutti i numeri di Mersenne sono primi: solo alcuni valori di \( n \) rendono il numero \( M_n \) primo.
Ad esempio:
- \( M_2 = 2^2 - 1 = 3 \) è primo.
- \( M_3 = 2^3 - 1 = 7 \) è primo.
- \( M_4 = 2^4 - 1 = 15 \) non è primo.
- \( M_5 = 2^5 - 1 = 31 \) è primo.
Questi numeri però hanno una particolarità interessante, se un numero di Mersenne \( M_n = 2^n - 1 \) è un numero primo, allora \( n \) è un numero primo.
Tuttavia, non è vero il contrario: se \( n \) è primo, questo non garantisce che \( M_n \) sia primo. Ad esempio, \( n = 11 \) è primo, ma \( M_{11} = 2^{11} - 1 = 2047 \), che non è primo (poiché \( 2047 = 23 \times 89 \)).
Questa particolarità rende i numeri di Mersenne molto utili nella ricerca dei numeri primi.
Invece di testare $ 2^n−1 $ per ogni $ n $, lo testiamo solo per numeri primi n, riducendo drasticamente il numero di calcoli.
Ecco una strategia per trovare numeri di Mersenne primi
- Scelgo solo numeri primi $ n $
- Calcolo il numero di Mersenne corrispondente $ M_n=2^n-1 $
- Effettuo un test di primalità per verificare se il numero $ M_n $ è effettivamente primo.
Questa strategia ha portato alla scoperta dei più grandi numeri primi mai conosciuti.
Purtroppo, uno dei limiti di questo metodo è che, anche se riduciamo il campo di ricerca a n primi, è comunque necessario calcolare il test di primalità a ciascun numero $ M_n $.
Nota. In ogni caso, vale la pena ricordare che non tutti i numeri primi sono numeri di Mersenne e non tutti i numeri di Mersenne sono numeri primi.
Note a margine
Alcune osservazioni e note a margine sui numeri primi.
- La differenza tra numeri primi e irriducibili
Nei numeri interi l'insieme dei numeri primi coincide con quello dei numeri irriducibili. Tuttavia, c'è una differenza tra primi e irriducibili. In altri anelli diversi dagli interi i primi non coincidono sempre con i numeri irriducibili. - Irrazionalità della radice dei numeri primi
La radice quadrata di un numero primo è un numero irrazionale.
E così via.
