Partizioni di un numero intero
Le partizioni di un numero intero n sono le successioni possibili di numeri k $$ k_1,k_2,..., k_t $$ con $$ k \ge k_2 \ge .... \ge k_t $$ tali che $$ k_1+k_2+...+k_t=n $$
Per costruire una partizione di un numero intero positivo, lo scompongo in una somma di interi positivi (addendi).
Il numero t degli addendi deve essere
$$ 1 \le t \le n $$
Nota. Posso rappresentare una partizione con il diagramma di Ferrers oppure con i tableau di Young. In questi appunti mi limito a usare soltanto i diagrammi di Ferrers.
Esempi di partizione
Esempio 1
Le partizioni del numero 3 sono
$$ 3 \\ 2+1 \\ 1+1+1 $$
Posso rappresentare le partizioni del numero 3 anche tramite il diagramma di Ferrers .
Dove ogni riga è un addendo.
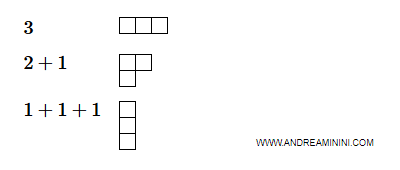
Esempio 2
Le partizioni del numero 4 sono
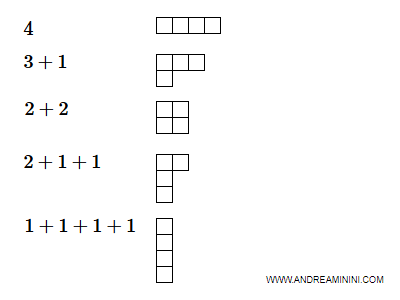
$$ 4 \\ 3+1 \\ 2+2 \\ 2+1+1 \\ 1+1+1+1 $$
Il diagramma di Ferrers del numero 4 è il seguente:
La funzione di partizione
La funzione di partizione p(n) indica il numero di partizioni di un unitero positivo n.
Esempi
La funzione di partizione del numero 3 è 3, perché il numero intero 3 ha tre partizioni distinte.
$$ p(3) = 3 $$
Nota. Le partizioni del numero 3 sono 3, 2+1, 1+1+1.
La funzione di partizione del numero 4 è 5, perché il numero intero 4 ha cinque partizioni.
$$ p(4) = 5 $$
Nota. Le partizioni del numero 4 sono 4, 3+1, 2+2, 2+1+1, 1+1+1+1.
Come si calcola la funzione di partizione di un intero?
Non c'è una formula per calcolare la funzione di partizione di qualsiasi intero.
Tuttavia, le funzioni di partizione degli interi compaiono come coefficienti in una seria detta funzione generatrice.
$$ \sum_{n=0}^{∞} p(n)x^n = p(0)x^0 + p(1)x^1 + p(2)x^2 +...+ p(n)x^n $$
Per calcolare il numero di partizioni di un intero n diviso in k parti uso questa formula ricorsiva:
$$ p_k(n) = p_{k-1}(n-1) + p_k (n-k) $$
Sapendo che per convenzione
$$ p(0)=p_0(0)=1 $$
$$ p_n(n)=1 $$
e se n>1
$$ p_1(n)=1 \\ p_{n-1}(n)=1 $$
Nota. Ho implementato questo algoritmo in python tramite una funzione ricorsiva per verificare se funziona. Effettivamente, l'algoritmo genera le k-partizioni per qualsiasi numero intero n. Tuttavia, diventa particolarmente complesso se il numero da elaborare è troppo alto.
