Il composto delle permutazioni nei gruppi simmetrici
Il composto è l'operazione che unisce le corrispondenze biunivoche di due gruppi simmetrici nello stesso insieme di riferimento X.
In altre parole, un composto (o composizione) è il prodotto di due permutazioni.
Esempio
Ho un insieme X
$$ X = ( 1, 2, 3, 4, 5 ) $$
e due corrispondenze biunivoche
$$ σ:X \rightarrow X $$
$$ t:X \rightarrow X $$
dove
$$ σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 5 & 2 & 1 & 3 \end{pmatrix} $$
$$ t = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 5 & 2 & 4 \end{pmatrix} $$
Il composto σ * t è
$$ σ * t = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 1 \end{pmatrix} $$
Per brevità d'ora in poi scrivero σ * t nella notazione σt senza indicare il simbolo dell'operatore.
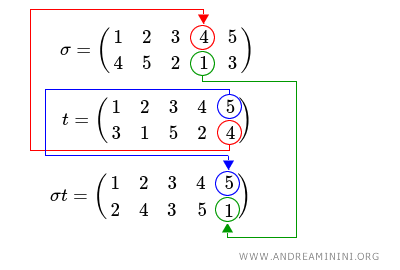
Spiegazione. Essendo una composizione del tipo f[g(x)], ovvero σ[t(x)], devo prima calcolare la permutazione più interna t (la seconda) e poi quella più esterna σ (la prima).
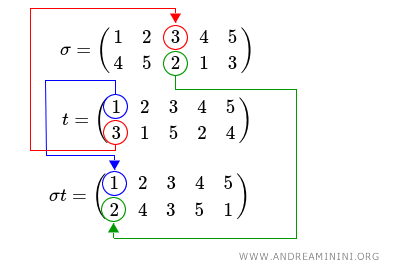
Una volta calcolata la transizione del primo elemento della permutazione t, procedo in modo sequenziale sul secondo elemento della permutazione t.
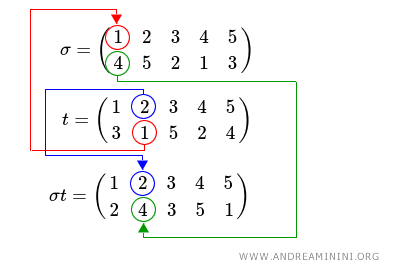
Poi sul terzo elemento della permutazione t e così via, fino a che non ho assegnato una nuova posizione a ciascun elemento.
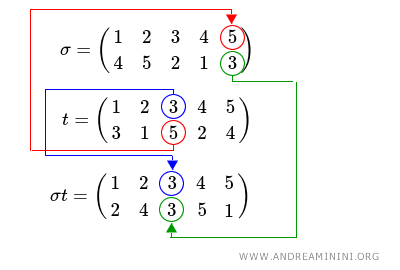
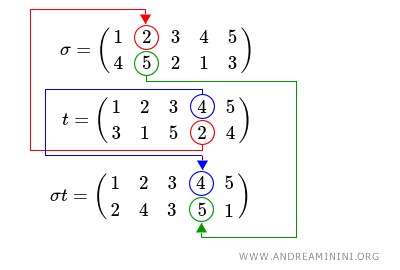
Il composto è un'operazione non abeliana perché non rispetta la proprietà commutativa.
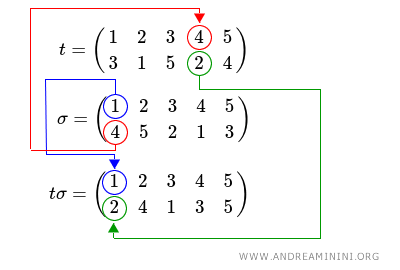
Se inverto l'ordine delle permutazioni il composto è diverso.
$$ t σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 5 \end{pmatrix} $$
Evito di fare tutti i passaggi per ottenere quest'ultimo risultato, mi limito a dimostrare solo il primo.
Nota. Soltanto se n ≤ 2, ovvero se ci sono due o un solo elemento nell'insieme X, il composto è un'operazione abeliana (commutativa). Ad esempio, considero queste due permutazioni con due elementi ciascuna: $$ σ = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ $$ t = \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix} $$ Il risultato della composizione σt $$ σ t = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ è lo stesso che ottengo nella composizione tσ $$ t σ = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ Quindi, l'operazione soddisfa la proprietà commutativa.
E così via.
