Il calcolo della radice quadrata a mano

Questo metodo è utile per calcolare la radice quadrata di un numero senza calcolatrice. E' stato ideato dal matematico Rafael Bombelli nel XVI secolo. E' abbastanza semplice ma per spiegarlo preferisco ricorrere a un esempio pratico.

Ad esempio, devo calcolare la radice quadrata di 1764

$$ \sqrt{1764} $$

Partendo da destra verso sinistra, separo con uno spazio le cifre del numero a coppie di due.

$$ 17 \ 64 $$

Nota. Se le cifre del numero sono dispari, aggiungo uno zero prima del numero. Ad esempio, se il numero nella radice quadrata è 19374 (ha cinque cifre), aggiungo uno zero davanti 019374 e poi lo suddivido in coppie di due cifre 01 93 74 come se fosse un numero telefonico.

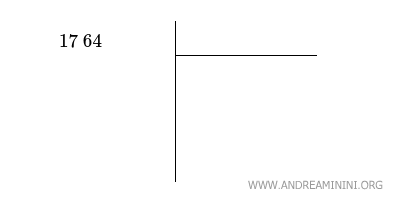
Traccio una linea verticale e una orizzontale, come se fosse una divisione.

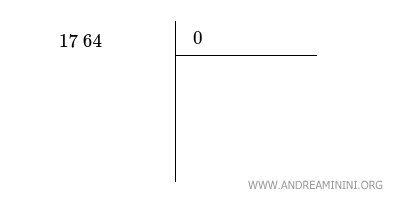
Nello spazio in alto a destra scrivo zero perché non conosco ancora il risultato.

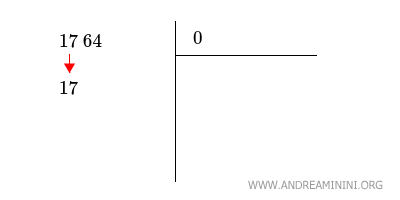
Faccio scendere la prima coppia di numeri a sinistra.

In questo caso è 17.

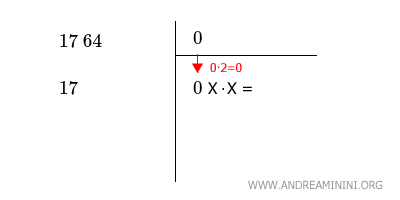
Nello spazio a destra faccio scendere il numero in alto a destra (0) moltiplicato per due (0·2=0) e gli affianco "x·x" dove x è un numero intero ancora incognito.

Nota per le scuole inferiori. Nella tabella sto usando il punto · come simbolo della moltiplicazione al posto del simbolo "x". E' la stessa cosa. Invece di scrivere 2x2=4 si scrive 2·2=4. Questa notazione si utilizza dalle scuole medie in poi. La lettera X è invece un numero intero che ancora non conosco. Può trattarsi di un numero a una o più cifre. Avrei potuto utilizzare qualsiasi altra lettera per indicarlo.

A questo punto devo trovare il numero 0x più grande che moltiplicato per x è uguale o inferiore a 17.

Lo zero davanti alla incognita 0x lo posso ignorare perché non aggiunge alcuna informazione.

Quindi, sapendo che 03·3=9, 04·4=16 e 05·5=25, il numero intero in questione è x=4.

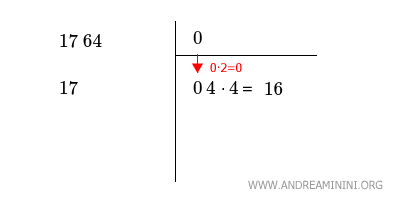
Quindi, aggiungo la cifra x=4 nello spazio in alto a destra e scrivo il risultato 16 nello spazio a sinistra in una nuova linea.

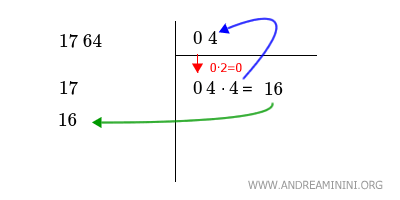
Poi, sempre a sinistra, tiro una linea e calcolo la differenza tra 17 e 16 scrivendola sotto la linea, in questo caso 17-16=1

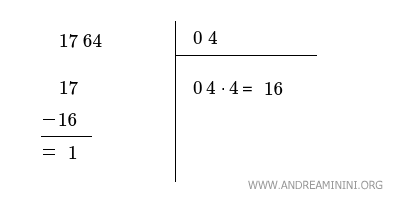
Infine, cancello lo spazio dei calcoli a destra e faccio scendere la coppia successiva del numero, ossia 64, e la scrivo a destra del numero 1.

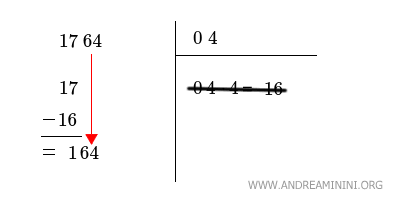
A questo punto il processo si ripete, faccio scendere il numero nell'angolo in basso a destra (04) e lo moltiplico per due (04·2=8) e aggiungo x·x, dove x è ancora una cifra incognita

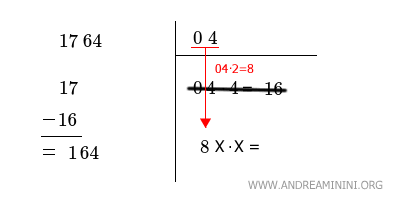
Ora devo trovare un numero intero a due cifre 8x più grande che moltiplicato per x è uguale o inferiore a 164.

Procedo per tentativi, provo a calcolare 80·0=0 utilizzando x=0, poi provo con 81·1=81 usando x=1, infine 82·2=164 con x=2 e mi fermo perché ho trovato ciò che cercavo.

In questo caso il valore dell'incognita è x=2 perché 82·2=164.

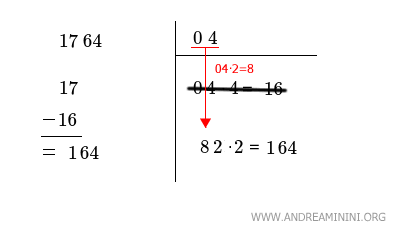
Quindi aggiungo la cifra x=2 nell'angolo in alto a destra e riporto 164 in una nuova riga nello spazio a sinistra.

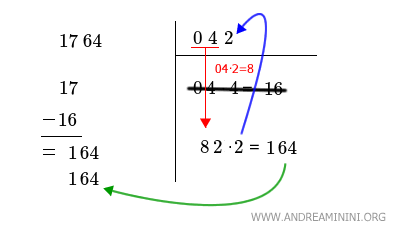
Infine calcolo la differenza 164-164=0

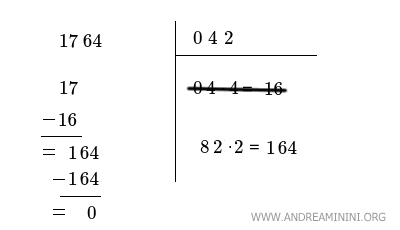
La differenza è nulla, questo vuol dire che il processo termina qui.

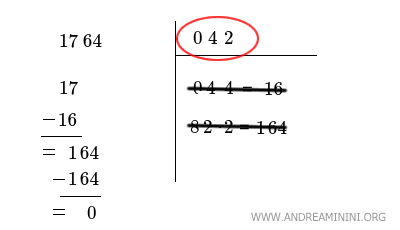
La radice quadrata di 1764 è il numero nell'angolo in alto a destra 042 ossia 42

$$ \sqrt{1764}=42 $$

Per verificarlo basta moltiplicare 42 per se stesso

$$ 42 \cdot 42 = 1764 $$

Nota. In questo caso ho trovato il risultato finito in due passaggi. Tuttavia, in altri casi l'algoritmo potrebbe iterare all'infinito. Pertanto è opportuno scegliere un grado di accuratezza accettabile dopo la virgola e terminare i calcoli una volta averlo raggiunto. Ad esempio, un risultato con 3 cifre decimali.

E cosa accade se la radice è un numero con la virgola?

Se il risultato finale è un numero decimale, utilizzo lo stesso metodo aggiungendo una virgola e due coppie di zeri al radicando.

Faccio un esempio pratico, calcolo la radice quadrata di 50.

$$ \sqrt{50} $$

In questo caso il radicando è una sola coppia di cifre.

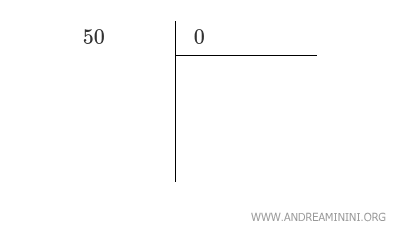
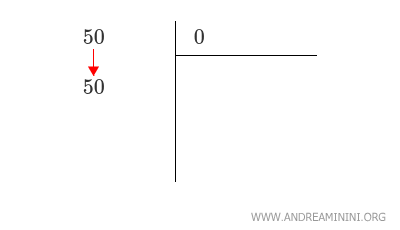
Faccio scendere la prima coppia di cifre (50) nella sezione a sinistra.

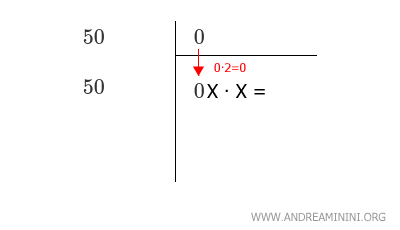
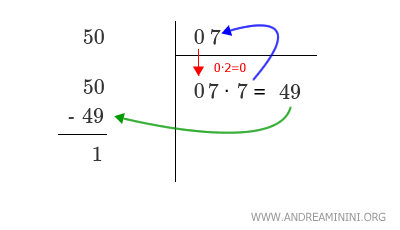
Faccio scendere il numero in alto a destra, lo moltiplico per due (0·2=0) e gli aggiungo x·x

Poi trovo il numero intero x più grande che moltiplicato per x (quindi per se stesso) è uguale o inferiore a 50.

Sapendo che 7·7=49 e 8·8=64, deduco che questo numero è x=7.

Quindi, scrivo 7 sopra la linea e sottraggo 49 da 50, ottenendo 1 come resto.

Poiché non ci sono altre cifre nel radicando (50), aggiungo una virgola e due zeri al numero originale (50,00).

Inoltre, aggiungo la virgola anche al numero in alto a destra.

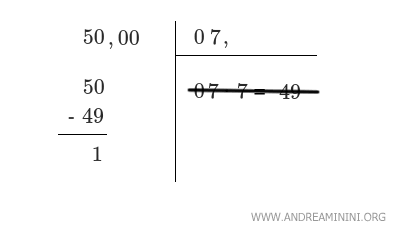
Nota. La virgola va scritta solo quando aggiungo la prima coppia di zeri decimali. Non le volte successive.

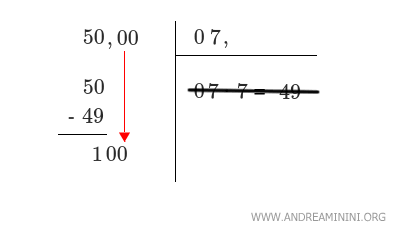
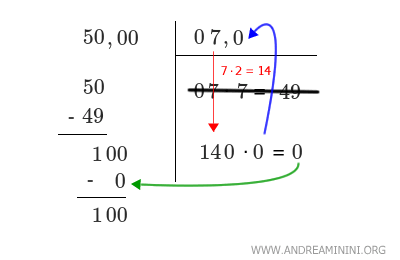
Ora porto giù i due zeri 00 a sinistra (senza la virgola) e li affianco a 1 ottenendo 100.

Poi faccio scendere il numero in alto a destra senza considerare la virgola, lo moltiplico per due 7·2 = 14 e gli aggiungo x·x.

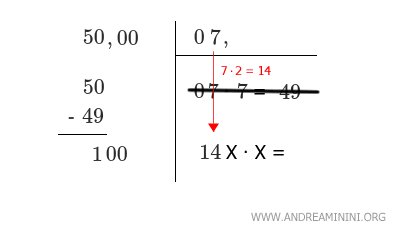
Vado per tentativi 142·2=284, 141·1=141, 140·0=0 che è inferiore a 100.

Quindi, il valore della x è x=0 e il risultato è 0.

Aggiungo 0 al numero in alto a destra e sottraggo 0 da 100 a sinistra.

Non essendoci altre coppie di numeri da far scendere, aggiungo altri due zeri al radicando e li faccio scendere.

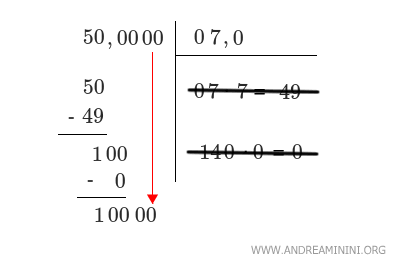
A questo punto, continuo la procedura fino a ottenere il numero decimale il risultato finale o un risultato accettabile.

Ora faccio scendere il numero in alto a destra senza considerare la virgola (070), lo moltiplico per due 70·2 = 140 e gli aggiungo x·x.

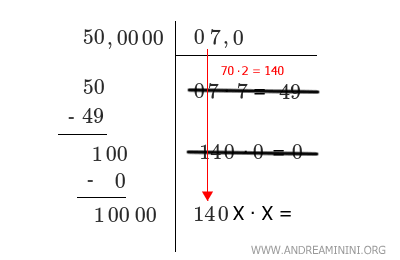
A questo punto devo trovare un numero intero x più grande tale che 140X·X sia inferiore o uguale a 10000.

Vado per tentativi, se x=6 allora 1406·6=8436

Se x=7 allora 1407·7=9849

Se x=8 allora 1408·8=11264 che è maggiore di 10000, quindi il risultato corretto è x=7.

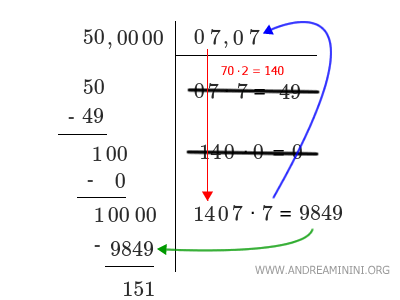
Al momento ho ottenuto come risultato un numero decimale con due cifre dopo la virgola.

$$ \sqrt{50} = 7,07 $$

Quindi, la radice quadrata di 50 è approssimativamente 7,07.

Per aumentare ulteriormente l'accuratezza del risultato, mi basterebbe ripetere la procedura, aggiungere e far scendere un'altra coppia di zeri 00 accanto a 151 e continuare i calcoli.

E così via.