Esercizio studio di funzione fratta 5

Devo studiare il grafico di questa funzione fratta

$$ f(x) = \frac{5x-1}{x^2-3x+2} $$

Per farlo utilizzo gli strumenti dell'analisi matematica procedendo step by step

Dominio

Per prima cosa studio il dominio della funzione.

La funzione è definita nell'insieme dei numeri reali, ad eccezione dei punti in cui si annulla il denominatore.

Le radici del denominatore x³-3x+2 sono x₁=1 e x₂=2

$$ x = \frac{-(-3) \pm \sqrt{(-3)^2-4(1)(2)}}{2(1)} $$

$$ x = \frac{3 \pm \sqrt{9-8}}{2} $$

$$ x = \frac{3 \pm \sqrt{1}}{2} $$

$$ x = \frac{3 \pm 1}{2} $$

$$ x = \begin{cases} \frac{3 - 1}{2} = 1 \\ \\ \frac{3 + 1}{2} = 2 \end{cases} $$

Quindi, il dominio della funzione è

$$ D_f = (- \infty, 1) \cup (1,2) \cup (2,\infty) $$

I punti in cui la funzione è indefinita sono x₁=1 e x₂=2

Intercette

Per trovare l'intercetta sull'asse delle ordinate (y) mi basta assegnare x=0 alla funzione f(x)

$$ y = f(0) = \frac{5 \cdot 0-1}{0^2-3 \cdot 0+2} = \frac{-1}{2} $$

La funzione interseca l'asse verticale nel punto (x;y)=(0;-1/2).

Per trovare l'intercetta sull'asse delle ascisse (x), invece, devo trovare il punto in cui la funzione si annulla y=0

$$ y = f(x) = 0 $$

$$ \frac{5x-1}{x^2-3x+2} = 0 $$

Per la proprietà invariantiva delle equazioni moltiplico per x²-3x+2 entrambi i membri

$$ \frac{5x-1}{x^2-3x+2} \cdot (x^2-3x+2) = 0 \cdot (x^2-3x+2) $$

$$ 5x-1 = 0 $$

In questo modo semplifico la ricerca.

A questo punto devo solo trovare la soluzione dell'equazione di primo grado 5x-1=0

$$ 5x-1=0 $$

$$ x = \frac{1}{5} $$

Pertanto, la funzione interseca l'asse x nel punto (x;y)=(1/5;0)

Segno questi due punti nel diagramma cartesiano

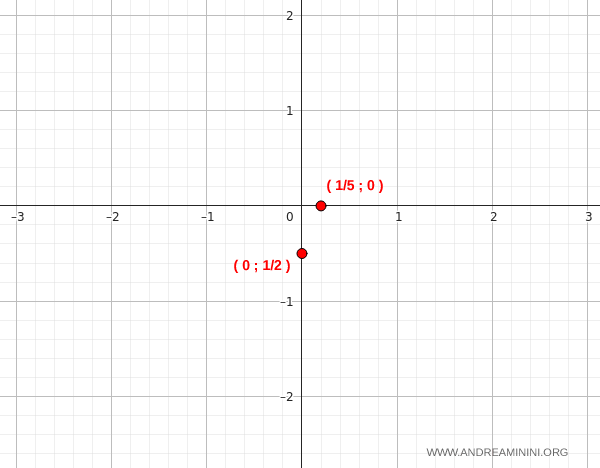
Studio del segno

Nello step seguente studio il segno della funzione

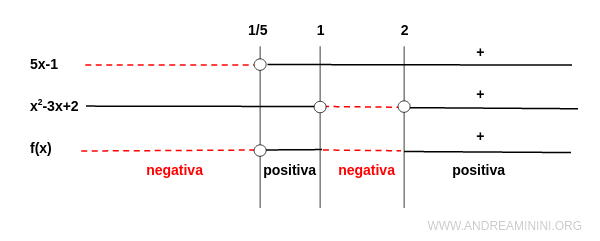
Analizzo il segno del numeratore e del denominatore della funzione fratta

• Il numeratore (5x-1) è positivo per ogni x>1/5, nullo in x=1/5 e negativo altrove
• Il denominatore (x2-3x+1) è una parabola rivolta verso l'alto che ha per radici x₁=1 e x₂=2. Le radici le ho già calcolate nello studio del dominio. Pertanto, il denominatore è negativo nell'intervallo (1;2) e positivo negli intervalli (-∞;1) e (2;∞)

Quindi, la funzione f(x) è negativa negli intervalli (-∞;1/5) e (1;2) ed è positiva negli intervalli (1/5;1) e (2;∞).

Utilizzo le informazioni fin qui raccolte per eliminare le zone del diagramma cartesiano dove non passa la funzione (in grigio).

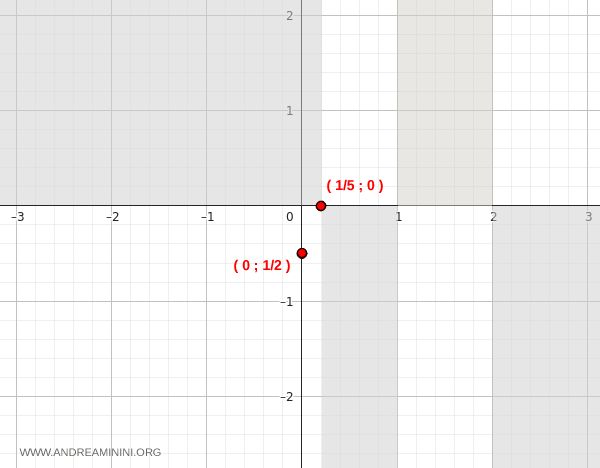
Asintoti

Asintoto orizzontale

Calcolo il limite della funzione per x che tende a infinito

$$ \lim_{x \rightarrow \infty } \frac{5x-1}{x^2-3x+2} = \frac{ \infty }{ \infty } $$

Il risultato è una forma indeterminata ∞/∞ che risolvo con il teorema di De L'Hopital

$$ \lim_{x \rightarrow \infty } \frac{D_x[5x-1]}{D_x[x^2-3x+2]} $$

$$ \lim_{x \rightarrow \infty } \frac{ 5 }{ 2x-3 } = 0^+ $$

Quindi al tendere x∼∞ la funzione tende a zero y→0⁺ da valori positivi

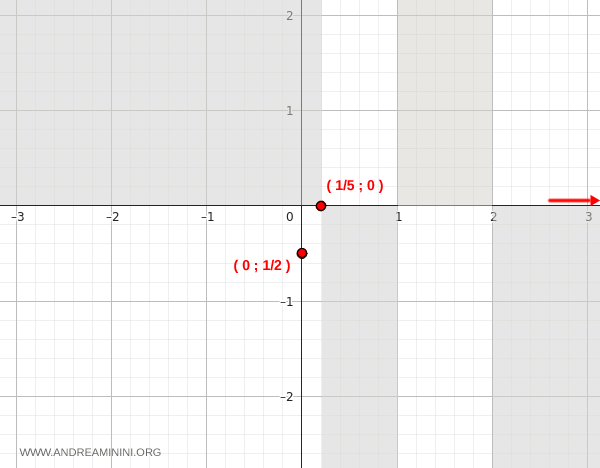
Ora calcolo il limite della funzione per x che tende a meno infinito

$$ \lim_{x \rightarrow -\infty } \frac{5x-1}{x^2-3x+2} = \frac{ -\infty }{ \infty } $$

Anche questa è una forma indeterminata risolvibile facilmente con De L'Hopital

$$ \lim_{x \rightarrow - \infty } \frac{D_x[5x-1]}{D_x[x^2-3x+2]} $$

$$ \lim_{x \rightarrow - \infty } \frac{5}{2x-3} = 0^+ $$

Quindi al tendere x∼-∞ la funzione tende a zero y→0^- da valori negativi

In conclusione, la funzione ha un asintoto orizzontale coincidente con l'asse delle x (y=0).

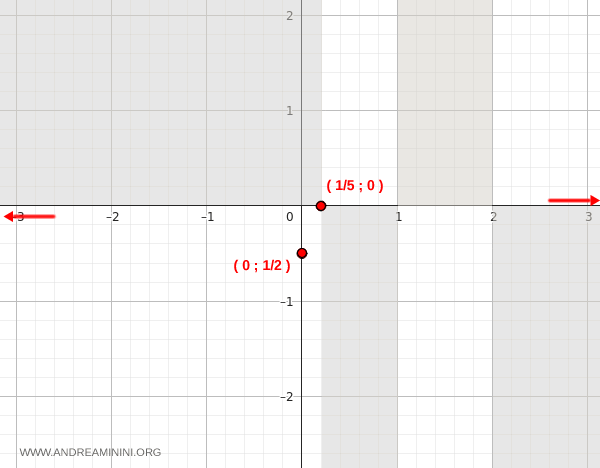
Asintoto verticale

Gli asintoti verticali possono trovarsi solo nei punti indefiniti della funzione.

In questo caso ci sono due punti in cui la funzione non è definita, sono x₁=1 e x₂=2

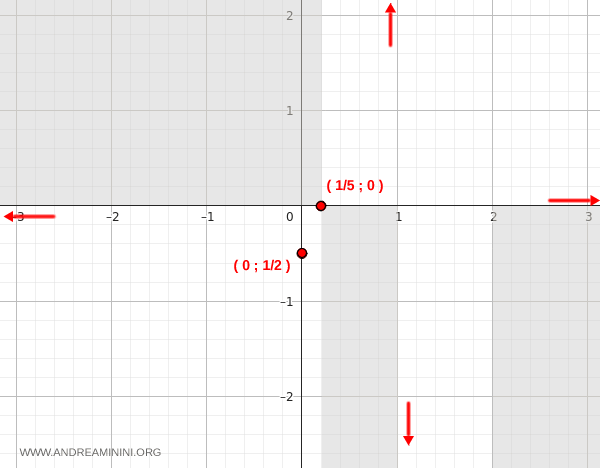
Verifico se esiste un asintoto verticale in x₁=1 calcolando il limite destro e sinistro della funzione per x che tende a 1

$$ \lim_{x \rightarrow 1^+ } \frac{5x-1}{x^2-3x+2} = \frac{4}{0^+} = -\infty $$

$$ \lim_{x \rightarrow 1^- } \frac{5x-1}{x^2-3x+2} = \frac{4}{0^-} = +\infty $$

I due limiti sono diversi, quindi in x₁=1 non c'è un asintoto verticale.

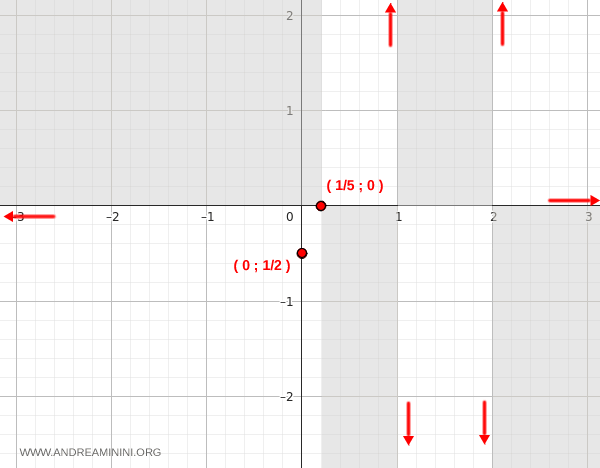
A questo punto verifico se esiste un asintoto verticale in x₁=2 calcolando il limite destro e sinistro della funzione per x che tende a 2

$$ \lim_{x \rightarrow 2^+ } \frac{5x-1}{x^2-3x+2} = \frac{9}{0^+} = +\infty $$

$$ \lim_{x \rightarrow 2^- } \frac{5x-1}{x^2-3x+2} = \frac{9}{0^-} = -\infty $$

Anche in questo caso i due limiti sono diversi, quindi in x₂=2 non c'è un asintoto verticale.

Crescenza e decrescenza

Per studiare i tratti in cui la funzione cresce o decresce, devo calcolare la derivata prima della funzione

$$ f'(x) = D_x [ \frac{5x-1}{x^2-3x+2} ] $$

Si tratta della derivata di un rapporto

$$ f'(x) = \frac{ D[5x-1] \cdot (x^2-3x+2) - (5x-1) \cdot D[x^2-3x+2]}{(x^2-3x+2)^2} $$

$$ f'(x) = \frac{ 5 \cdot (x^2-3x+2) - (5x-1) \cdot (2x-3)}{(x^2-3x+2)^2} $$

$$ f'(x) = \frac{ 5x^2-15x+10 - 10x^2+15x +2x-3}{(x^2-3x+2)^2} $$

Pertanto, la derivata prima della funzione è

$$ f'(x) = \frac{ -5x^2+2x+7}{(x^2-3x+2)^2} $$

Ora studio il segno della derivata prima

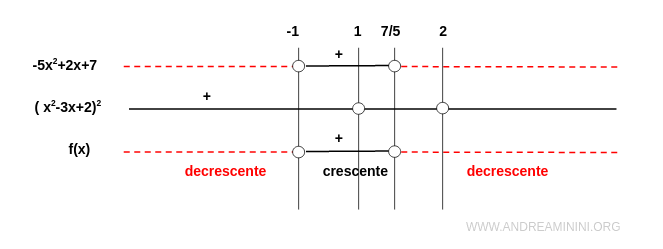
Nota. Il numeratore -5x²+2x+7 è una parabola rivolta verso il basso perché a=-5<0 che ha le radici in $$ x = \frac{-2 \pm \sqrt{2^2-4(-5)(7)} }{2(-5)} = \frac{-2 \pm \sqrt{4+140} }{-10} $$ $$ x = \frac{-2 \pm \sqrt{144} }{-10} = \frac{-2 \pm 12}{-10} $$ $$ x = \begin{cases} \frac{-2 - 12}{-10} = \frac{-14}{-10} = \frac{7}{5} \\ \\ \frac{-2 + 12}{-10} = \frac{10}{-10} = -1 \end{cases} $$

Quindi, la funzione decresce nell'intervallo (-∞,-1) e (7/5,∞) mentre cresce nell'intervallo (-1, 7/5).

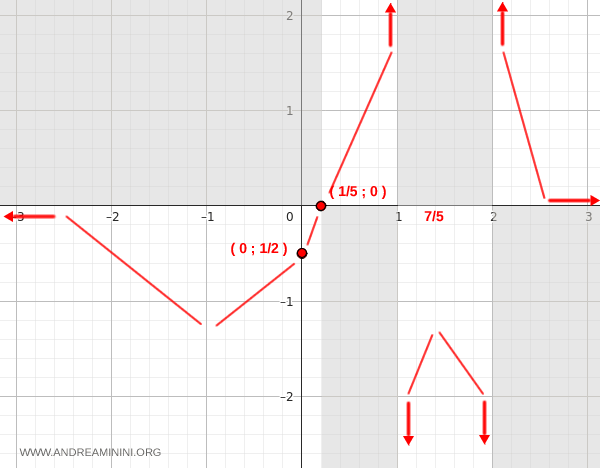
I punti dove si annulla la derivata prima (punti stazionari) sono potenziali punti di minimo a massimo locale.

In questo caso i punti stazionari sono x=-1 e x=7/5

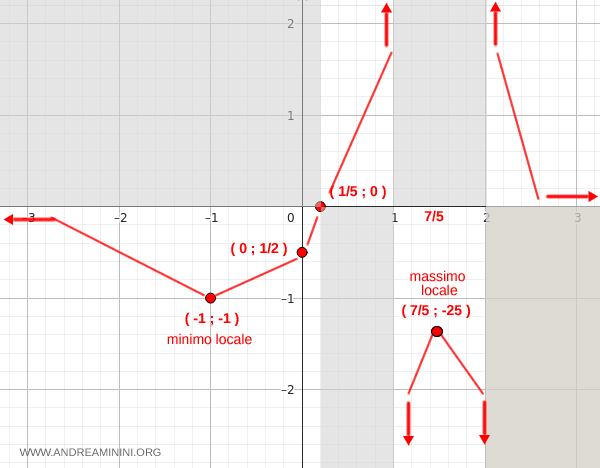
• Nel punto x=-1 si trova un minimo locale perché la funzione decresce a sinistra e cresce a destra. Sapendo che x=-1, il valore della y è -1. Quindi il punto di minimo locale si trova alle coordinate (x;y)=(-1;-1) $$ \frac{5(-1)-1}{(-1)^2-3(-1)+2} =\frac{-6}{6} = -1 $$
• Nel punto x=7/5 si trova un massimo locale perché la funzione cresce a sinistra e decresce a destra. Sapendo che x=7/5, il valore della y è. Quindi il punto di minimo locale si trova alle coordinate (x;y)=(7/5;-25) $$ \frac{5(7/5)-1}{(7/5)^2-3(7/5)+2} =\frac{6}{\frac{49}{25}- \frac{21}{5} +2 } = \frac{6}{ \frac{49-105+50}{25} } = \frac{6}{ \frac{-6}{25} } = 6 \cdot \frac{25}{-6} = -25$$

Convessità e concavità

Per studiare i tratti in cui la funzione è convessa o concava devo calcolare la derivata seconda della funzione

$$ f''(x) = D_x [ f'(x) ] $$

$$ f''(x) = D_x [ \frac{ -5x^2+2x+7}{(x^2-3x+2)^2} ] $$

E' la derivata di un rapporto di funzioni

$$ f''(x) = \frac{ D_x[ -5x^2+2x+7 ] \cdot (x^2-3x+2)^2 - ( -5x^2+2x+7 ) \cdot D_x[(x^2-3x+2)^2 ] }{[(x^2-3x+2)^2]^2} $$

$$ f''(x) = \frac{ (-10x +2 ) \cdot (x^2-3x+2)^2 - ( -5x^2+2x+7 ) \cdot ( 2 \cdot (x^2-3x+2) \cdot (2x-3) ) }{(x^2-3x+2)^4} $$

$$ f''(x) = \frac{ (-10x +2 ) \cdot (x^2-3x+2)^{\cancel{2}1} - ( -5x^2+2x+7 ) \cdot ( 2 \cdot \require{cancel} \cancel{ (x^2-3x+2) } \cdot (2x-3) ) }{(x^2-3x+2)^{ \cancel{4} 3}} $$

$$ f''(x) = \frac{ (-10x^3 +30x^2-20x +2x^2 -6x+4)) - \\ (-5x^2+2x+7) \cdot (4x-6) }{(x^2-3x+2)^3} $$

$$ f''(x) = \frac{ (-10x^3 +32x^2-26x +4) - \\ ( -20x^3 + 30x^2 +8x^2-12x+28x-42 ) }{(x^2-3x+2)^3}$$

$$ f''(x) = \frac{ -10x^3 +32x^2-26x +4 +20x^3 - 30x^2 -8x^2+12x-28x+42 }{(x^2-3x+2)^3}$$

$$ f''(x) = \frac{ 10x^3 -6x^2-42x + 46 }{(x^2-3x+2)^3}$$

In questo caso il numeratore è un'equazione di 3° grado non semplificabile.

Tuttavia, analizzando i valori dell'equazione 10x3-6x2-42x+46 nell'intervallo (-2,2) posso facilmente dedurre che è positiva nell'intervallo (-2, +∞) e diventa negativa per qualche valore β<-2

Quindi, lo studio del segno della derivata seconda è il seguente

La funzione f(x) è concava nell'intervallo (-∞, β) dove β<-2.

Poi diventa convessa nell'intervallo (β,1), di nuovo concava nell'intervallo (1,2) e di nuovo convessa nell'intervallo (2,∞)

Nell'intorno del punto x=β la funzione è concava a destra e convessa a sinistra. Quindi, in questo punto c'è un punto di flesso.

Il grafico della funzione è il seguente

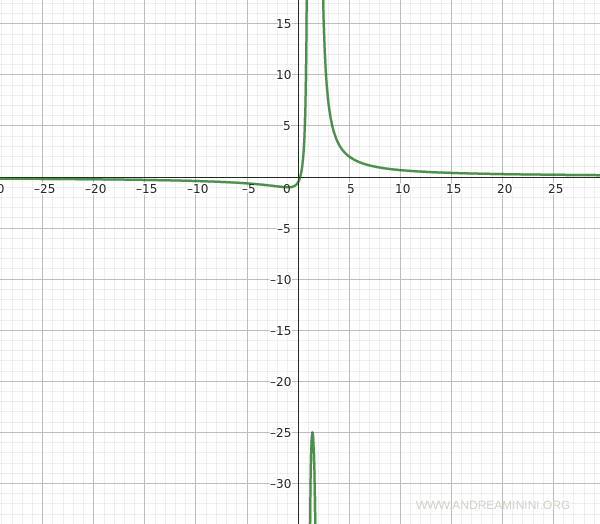
E così via.