Esercizio studio di funzione esponenziale 11
Devo studiare la funzione esponenziale
$$ f(x) = \frac{x}{e^x} $$
Comincio l'analisi studiando il dominio della funzione.
Dominio
La funzione esponenziale ex non si annulla mai, quindi il dominio della funzione coincide con l'insieme dei numeri reali.
$$ D_f = ( -\infty , \infty ) $$
I punti indefiniti
Non ci sono punti indefiniti, perché la funzione è definita nell'insieme dei numeri reali.
Asintoti orizzontali
Studio il limite della funzione per x che tende a più infinito.
$$ \lim_{x \rightarrow \infty} \frac{x}{e^x} = \frac{\infty}{\infty} $$
Il risultato del limite è una forma indeterminata. Per risolverla utilizzo il teorema di De L'Hopital.
$$ \lim_{x \rightarrow \infty} \frac{D[x]}{D[e^x]} $$
$$ \lim_{x \rightarrow \infty} \frac{1}{e^x} = 0^+ $$
Pertanto, la funzione tende a zero quando x tende a infinito.
Ora studio il limite della funzione per x che tende a meno infinito.
$$ \lim_{x \rightarrow \infty} \frac{x}{e^x} = \frac{-\infty}{0^+} = - \infty $$
Quindi, la funzione tende a meno infinito (y→-∞) quando x→-∞.
Asintoti verticali
Non essendoci punti indefiniti, non ci sono nemmeno asintoti verticali.
Intercette
Per trovare l'intercetta con l'asse y, mi basta assegnare il valore x=0 alla funzione.
$$ f(0) = \frac{0}{e^0} = \frac{0}{1} = 0 $$
Quindi, la funzione passa per l'origine degli assi ossia per il punto (x;y)=(0;0)
Per trovare l'intercetta con l'asse x devo risolvere l'equazione fratta
$$ f(x) = 0 $$
$$ \frac{x}{e^x} = 0 $$
Moltiplico entrambi i membri per ex
$$ \frac{x}{e^x} \cdot e^x = 0 \cdot e^x $$
$$ x = 0 $$
Questo dimostra che la funzione interseca l'asse x una sola volta nel punto (x,y)=(0,0)
Studio del segno
A questo punto procedo con lo studio del segno della funzione fratta.
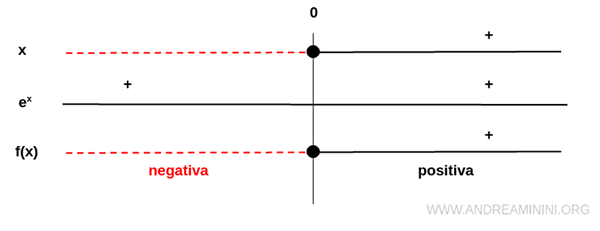
Il denominatore ex è sempre positivo mentre il numeratore x è positivo solo per x>0
Quindi, la funzione è negativa nell'intervallo (-∞,0) e positiva nell'intervallo (0,∞).
Elimino le aree del diagramma cartesiano in cui la funzione non passa

Studio della crescenza e decrescenza
Per studiare i tratti in cui la funzione cresce e quelli in cui decresce, devo calcolare la sua derivata prima.
$$ D_x [ \frac{x}{e^x} ] = \frac{D[x] \cdot e^x - x D[e^x]}{[e^x]^2} $$
$$ D_x [ \frac{x}{e^x} ] = \frac{1 \cdot e^x - x e^x}{[e^x]^2} $$
$$ D_x [ \frac{x}{e^x} ] = \frac{ e^x - x e^x}{[e^x]^2} $$
$$ D_x [ \frac{x}{e^x} ] = \frac{ e^x (1 - x)}{[e^x]^2} $$
$$ D_x [ \frac{x}{e^x} ] = \frac{1 - x}{e^x} $$
In alternativa, per calcolare la derivata prima posso trasformare la funzione in questa forma equivalente e applicare la regola di derivazione del prodotto. $$ D_x [ x e^{-x} ] = D[x] e^{-x} + x D[e^{-x}] $$ $$ D_x [ x e^{-x} ] = 1 \cdot e^{-x} + x \cdot (-1) \cdot e^{-x} $$ $$ D_x [ x e^{-x} ] = e^{-x} - x e^{-x} $$ $$ D_x [ x e^{-x} ] = e^{-x} \cdot (1- x) $$ $$ D_x [ x e^{-x} ] = \frac{1-x}{e^x} $$ Il risultato finale è sempre lo stesso.
A questo punto studio il segno della derivata prima
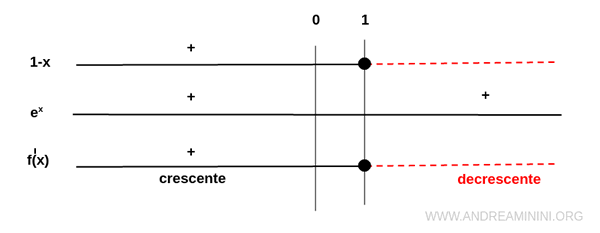
La derivata prima f'(x) è positiva nell'intervallo (-∞,1) e negativa nell'intervallo (1,∞).
Quindi, la funzione f(x) è crescente nell'intervallo (-∞,1) e decrescente nell'intervallo (1,∞).
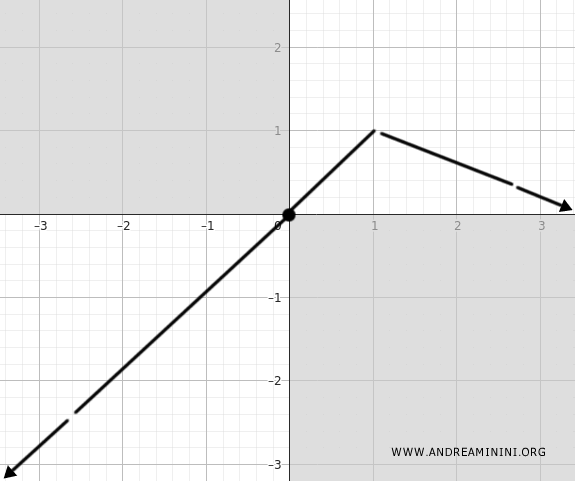
Nel punto x=1 la derivata prima si annulla f'(x)=0 passando da crescente a decrescente.
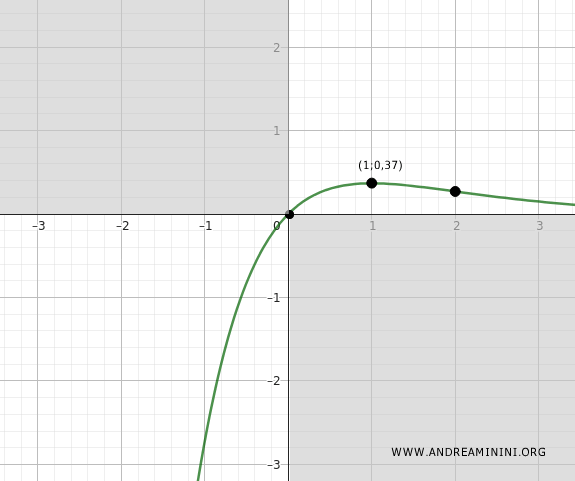
Quindi, nel punto x=1 la funzione ha un massimo locale.
Per trovare le coordinate del punto calcolo la funzione y=f(x) nel punto x=1
$$ f(1) = \frac{1}{e^1} = 0,37 $$
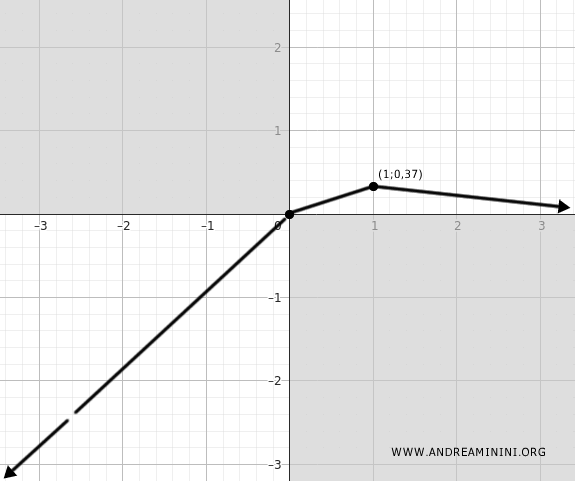
Pertanto, le coordinate del punto di massimo sono (x;y)=(1;0,37)
Studio della concavità, convessità e flessi
Per studiare i tratti in cui la funzione è concava o convessa e la presenza di eventuali flessi, calcolo la derivata seconda della funzione ossia la derivata della derivata prima che già conosco.
$$ f''(x) = D_x [ f'(x) ] $$
$$ f''(x) = D_x [ \frac{1 - x}{e^x} ] $$
$$ f''(x) = \frac{D_x[1 - x] \cdot e^x - (1-x) \cdot D_x[e^x]}{[e^x]^2} $$
$$ f''(x) = \frac{(-1) \cdot e^x - (1-x) \cdot e^x}{[e^x]^2} $$
$$ f''(x) = \frac{-e^x - e^x + xe^x}{[e^x]^2} $$
$$ f''(x) = \frac{-2e^x + xe^x}{[e^x]^2} $$
$$ f''(x) = \frac{e^x \cdot (x-2)}{[e^x]^2} $$
$$ f''(x) = \frac{x-2}{e^x} $$
A questo punto studio il segno della derivata seconda f''(x)
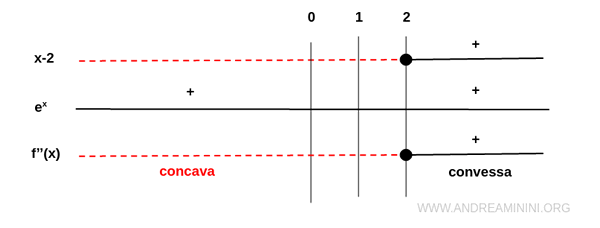
La derivata seconda è negativa nell'intervallo (-∞,2) e positiva nell'intervallo (2,∞).
Quindi, la funzione f(x) è concava nell'intervallo (-∞,2) e convessa nell'intervallo (2,∞).
Nel punto x=2 la derivata si annulla, pertanto si verifica un flesso.
Per trovare la coordinata y del flesso basta sostituire x=2 nella funzione f(x)
$$ f(2) = \frac{2}{e^2} = 0,27 $$
Quindi, il punto di flesso si verifica alle coordinate (x;y)=(2;0,27)
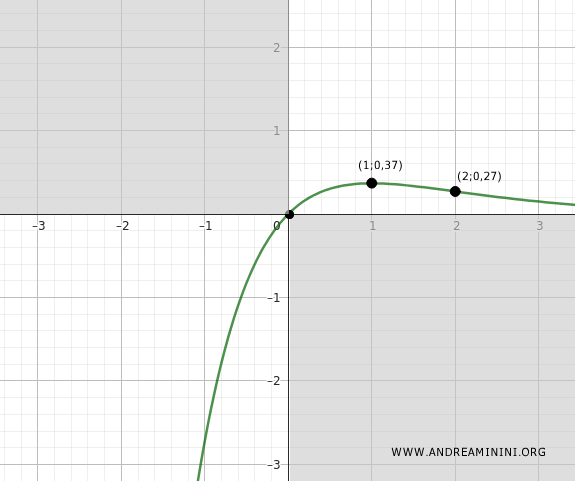
E così via.
