Esercizio studio di funzione 8
Devo studiare la funzione esponenziale
$$ f(x)= e^{\frac{1}{x}} $$
Studio la funzione tramite gli strumenti dell'analisi matematica
Dominio
La funzione è definita in tutto l'insieme dei numeri reali tranne che in x=0.
$$ D_f = R - \{ 0 \} $$
In x=0 si verifica una divisione per zero nelll'esponente (1/x).
Pertanto, x=0 è un punto indefinito della funzione.
Intercette
Sapendo che in x=0 la funzione non è definita, non calcolo l'intercetta con l'asse delle x
Verifico se esiste l'intercetta con l'asse y ponendo
$$ e^{\frac{1}{x}} = 0 $$
Per risolvere quest'ultima equazione esponenziale, utilizzo la proprietà invariantiva delle equazioni applicando il logaritmo naturale a entrambi i membri
$$ \log e^{\frac{1}{x}} = \log 0 $$
Il logaritmo naturale è la funzione inversa dell'esponenziale.
Quindi, posso semplificare il membro di sinistra.
$$ \frac{1}{x} = \log 0 $$
Sapendo che il logaritmo di zero non esiste, deduco che non esiste nemmeno l'intercetta con l'asse y.
Studio del segno
Lo studio il segno della funzione è molto semplice.
La funzione esponenziale è sempre positiva in tutto il suo campo di definizione.
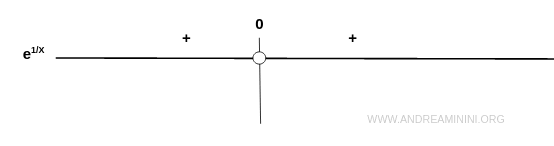
Quindi, la funzione passa per il primo e il secondo quadrante del diagramma cartesiano.
Asintoti orizzontali
Per studiare il comportamento asintotico calcolo il limite della funzione per x che tende a più infinito
$$ \lim_{x \rightarrow \infty} e^{\frac{1}{x}} = 1^+ $$
Nota. Quando x tende a infinito, l'esponente dell'esponenziale tende a zero. Quindi, la funzione esponenziale tende a 1.
Poi studio il segno per x che tende a meno infinito.
$$ \lim_{x \rightarrow - \infty} e^{\frac{1}{x}} = 1^- $$
Nota. Quando x tende a meno infinito, l'esponente tende a 0^- da sinistra. Quindi la funzione esponenziale tende a 1.
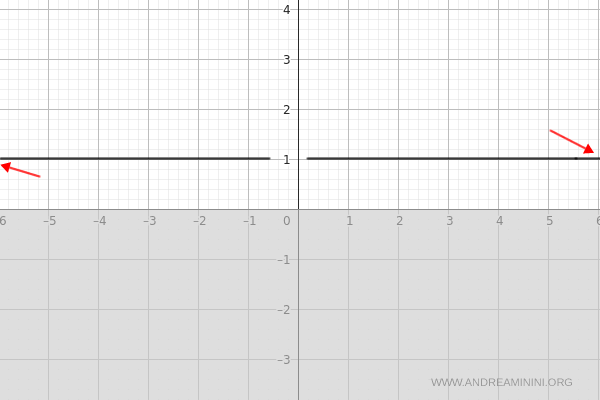
I due limiti corrispondono.
Pertanto, in y=1 la funzione ha un asintoto orizzontale.
Asintoti verticali
Gli asintoti verticali possono trovarsi solo nei punti in cui la funzione non è definita.
In questo caso la funzione non è definita in x=0
Studio il limite della funzione per che tende a x=0 da destra e da sinistra
$$ \lim_{x \rightarrow 0^+} e^{\frac{1}{x}} = +\infty $$
$$ \lim_{x \rightarrow 0^-} e^{\frac{1}{x}} = 0 $$
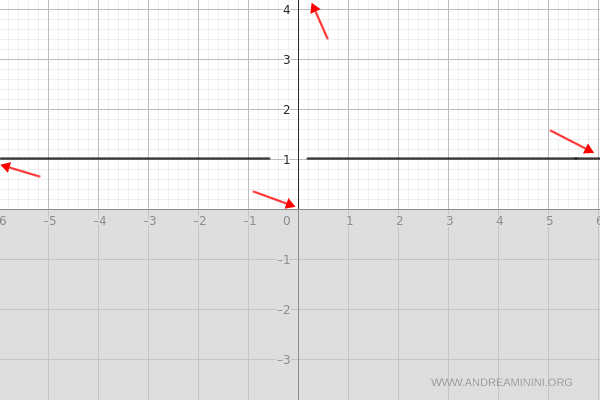
I due limiti non corrispondono.
Quindi, la funzione non ha un asintoto verticale in x=0.
Crescenza e decrescenza
Per studiare la crescenza e la decrescenza della funzione devo calcolare la derivata prima della funzione
$$ f'(x) = D_x[ e^{\frac{1}{x}} ] $$
Si tratta di una derivata composta
$$ f'(x)= e^{\frac{1}{x}} \cdot D[ \frac{1}{x} ] $$
$$ f'(x) = e^{\frac{1}{x}} \cdot D[ x^{-1} ] $$
$$ f'(x) = e^{\frac{1}{x}} \cdot (-1) x^{-2} $$
$$ f'(x) = -e^{\frac{1}{x}} \cdot \frac{1}{x^2} $$
$$ f'(x) = - \frac{e^{\frac{1}{x}}}{x^2} $$
Studio il segno della derivata prima.
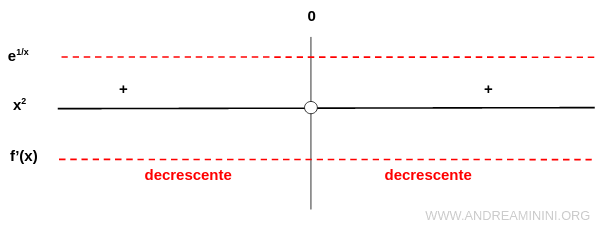
La derivata prima è sempre negativa in tutto il campo di definizione della funzione.
Quindi, la funzione f(x) è sempre decrescente.
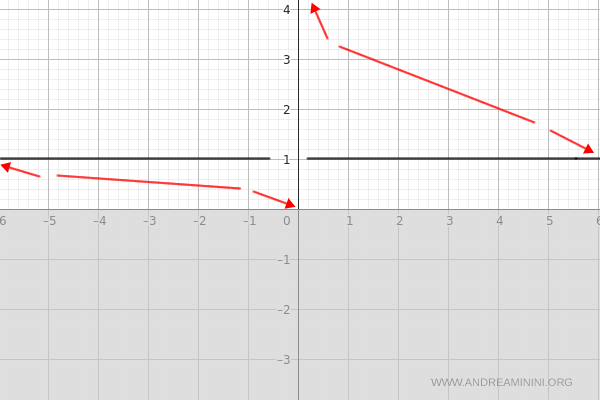
Punti di minimo e massimo locale
La derivata prima della funzione non si annulla mai.
Quindi, non ci sono punti di minimo e punti di massimo locali.
Convessità e concavità
Per studiare la convessità e la concavità della funzione devo calcolare la derivata seconda della funzione, ossia la derivata della derivata prima.
$$ f''(x) = D_x[ f'(x) ] $$
$$ f''(x) = D_x[ - \frac{e^{\frac{1}{x}}}{x^2} ] $$
Applico la regola di derivazione del rapporto
$$ f''(x) = - \frac{D_x[ e^{\frac{1}{x}}] \cdot x^2 - e^{\frac{1}{x}} \cdot D_x[x^2] }{[x^2]^2} $$
$$ f''(x) = - \frac{e^{\frac{1}{x}} \cdot ( - \frac{1}{x^2} ) \cdot x^2 - e^{\frac{1}{x}} \cdot 2x }{x^4} $$
$$ f''(x) = - \frac{-e^{\frac{1}{x}} - e^{\frac{1}{x}} \cdot 2x }{x^4} $$
$$ f''(x) = \frac{e^{\frac{1}{x}} + e^{\frac{1}{x}} \cdot 2x }{x^4} $$
$$ f''(x) = \frac{e^{\frac{1}{x}} \cdot (1+2x) }{x^4} $$
A questo punto studio il segno della derivata seconda
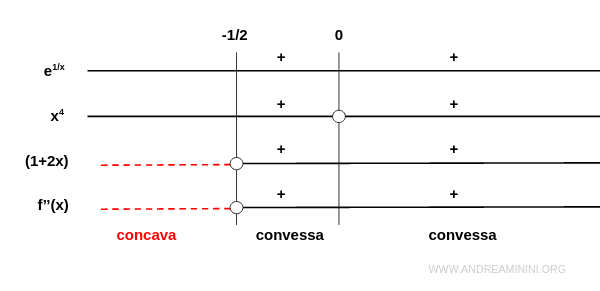
Dallo studio del segno deduco che
- la funzione è concava nell'intervallo (-∞;1/2)
- la funzione è convessa nell'intervallo (-1/2;+∞)
Inoltre, quando x=-1/2 la funzione ha un punto di flesso.
Pertanto, il grafico della funzione è il seguente:
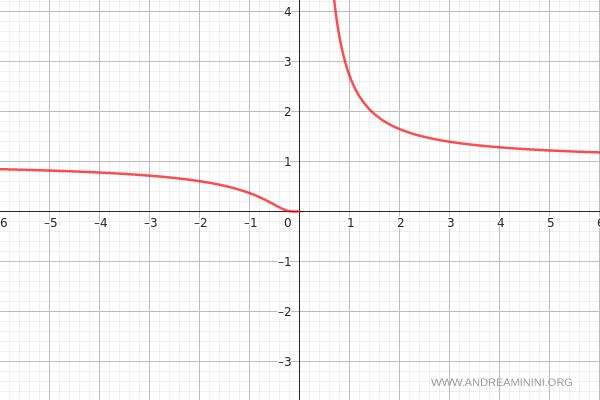
E così via.
