Esercizio studio di funzione 7

Devo studiare la funzione esponenziale

$$e^x + e^{-x}$$

Inizio lo studio analizzando il dominio della funzione

Dominio

Per studiare il dominio riscrivo la funzione in un'espressione equivalente più comoda

$$f(x) =e^x + e^{-x}$$

$$f(x) =e^x + \frac{1}{e^{x}}$$

$$f(x) =\frac{e^x \cdot e^x + 1}{e^{x}}$$

$$f(x) =\frac{e^{2x} + 1}{e^{x}}$$

Ora si tratta di una funzione fratta.

La funzione è definita nell'insieme dei numeri reali, perché la funzione esponenziale è sempre positiva. Quindi, il denominatore non si annulla mai.

Il dominio della funzione coincide con l'insieme dei numeri reali R.

$$D_f = R$$

Studio del segno

La funzione f(x)=(e^2x+1)/e^x è sempre positiva nell'insieme dei numeri reali

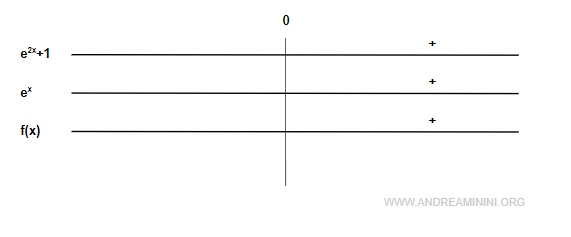
Intercetta con l'asse x

Dallo studio del segno so già che la funzione è sempre positiva e non ci sono radici. Quindi non interseca mai l'asse x.

Tuttavia, per completezza svolgo anche questo calcolo.

Per verificare se la funzione interseca l'asse x devo risolvere la seguene equazione y=f(x)=0

$$\frac{e^{2x} + 1}{e^{x}} = 0$$

Applico la proprietà invariantiva delle equazioni moltiplicando entrambi i membri per e^x

$$\frac{e^{2x} + 1}{e^{x}} \cdot e^x = 0 \cdot e^x$$

$$e^{2x} + 1 = 0$$

$$e^{2x} = -1$$

Applico la proprietà invariantiva applicando il logaritmo naturale a entrambi i membri

$$\log{ e^2x } = \log{ -1 }$$

$$2x = \log{ -1 }$$

L'equazione non ha soluzioni perché il logaritmo è definito solo se l'argomento è un numero positivo.

Pertanto, la funzione non ha intercette con l'asse x.

Intercetta con l'asse y

Per trovare l'intercetta con l'asse y basta sostituire x=0 nella funzione

$$f(x) = \frac{e^{2x} + 1}{e^{x}}$$

$$f(0) = \frac{e^{2 \cdot 0} + 1}{e^{0}}$$

$$f(0) = \frac{e^{0} + 1}{e^{0}}$$

Sapendo che l'esponenziale e⁰=1

$$f(0) = \frac{1 + 1}{1}$$

$$f(0) = \frac{2}{1} = 0$$

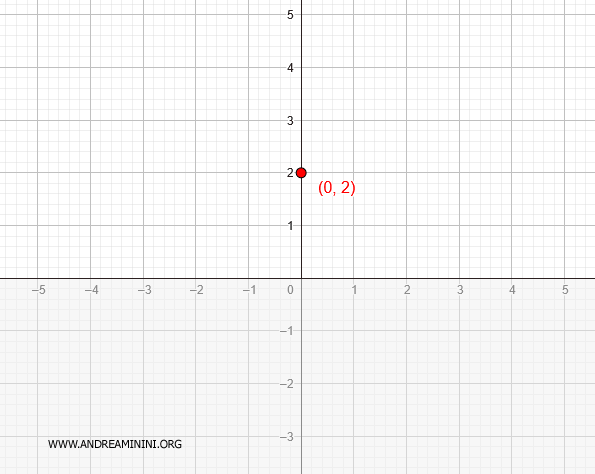
Pertanto, la funzione interseca l'asse y nel punto (x;y)=(0;2)

Utilizzo le informazioni fin qui raccolte per cominciare a delimitare le aree del diagramma cartesiano e i punti dove passa la funzione.

Asintoti verticali e orizzontali

La funzione è continua e definita in ogni punto del suo dominio. Quindi non ci sono asintoti verticali.

Per trovare gli asintoti orizzontali calcolo il limite destro e sinistro della funzione.

Il limite destro della funzione è più infinito (+∞)

$$\lim_{x \rightarrow \infty} e^x + e^{-x} = \lim_{x \rightarrow \infty} e^x + \lim_{x \rightarrow \infty}e^{-x} = \infty - 0 = \infty$$

Il limite sinistro della funzione è più infinito (+∞)

$$\lim_{x \rightarrow - \infty} e^x + e^{-x} = \lim_{x \rightarrow \infty} e^x + \lim_{x \rightarrow \infty}e^{-x} = 0 + \infty = \infty$$

Pertanto, non ci sono asintoti orizzontali.

Il comportamento asintotico della funzione tende a più infinito sia per x→∞ e sia per x→-∞

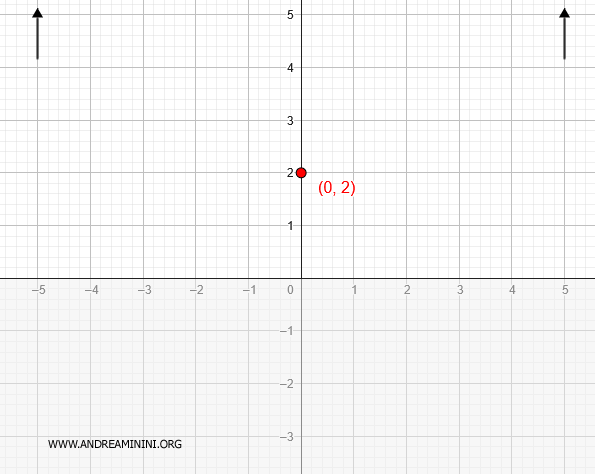
Crescenza e decrescenza

Per studiare l'andamento della funzione devo calcolare la derivata prima e studiarne il segno

Calcolo la derivata prima della funzione rispetto a x

Scelgo la funzione nell'espressione equivalente f(x)=e^x+e^-x perché mi semplifica i passaggi

$$f'(x) = D_x[ e^x + e^{-x} ]$$

$$f'(x) = D_x[ e^x ] + D_x[ e^{-x} ]$$

Sapendo che la derivata di D[e^x]=e^x e D[e^-x]=-e^-x perché si tratta di una funzione composta D[e^x]·D[x]

$$f'(x) = e^x - e^{-x}$$

Nota. Avrei raggiunto lo stesso risultato anche derivando la funzione nell'altra espressione ma con più passaggi. $$f'(x) = D_x[ \frac{e^{2x} + 1}{e^{x}} ]$$ Utilizzo la regola di derivazione di un rapporto di funzioni $$f'(x) = \frac{D_x[ e^{2x} + 1 ] \cdot e^x - (e^{2x} +1) \cdot D_x[e^x] } { ( e^{x} )^2 }$$ $$f'(x) = \frac{( e^{2x} \cdot 2 ) \cdot e^x - (e^{2x} +1) \cdot e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ 2 \cdot e^{2x} \cdot e^x - e^{2x}e^x - e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ 2 \cdot e^{2x+x} - e^{2x+x} - e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ 2 \cdot e^{3x} - e^{3x} - e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ e^{3x} - e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ e^{2x} \cdot e^x - e^x } { ( e^{x} )^2 }$$ $$f'(x) = \frac{ e^{2x} - 1 } { e^{x} }$$ $$f'(x) = \frac{ e^{2x}}{e^{x}} - \frac{ 1 } { e^{x} }$$ $$f'(x) = \frac{ e^{x} \cdot e^x}{e^{x}} - e^{-x}$$ $$f'(x) = e^x - e^{-x}$$

Poi studio il segno della derivata prima

$$f'(x) = e^x - e^{-x}$$

Trrasformo l'espressione in un rapporto equivalente

$$f'(x) = e^x - \frac{1}{e^x} = \frac{e^x \cdot e^x -1}{e^x} = \frac{e^{2x}-1}{e^x}$$

In questo modo è più facile studiare il segno

La derivata prima è negativa nell'intervallo (-∞,0) e positiva nell'intervallo (0,∞)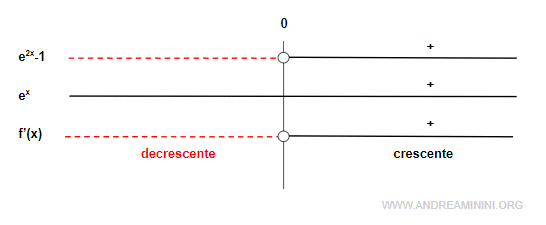

Quindi, la funzione decresce nell'intervallo (-∞,0) e cresce nell'intervallo (0,∞)

Aggiorno la costruzione del grafico nel diagramma cartesiano inserendo le tendenze.

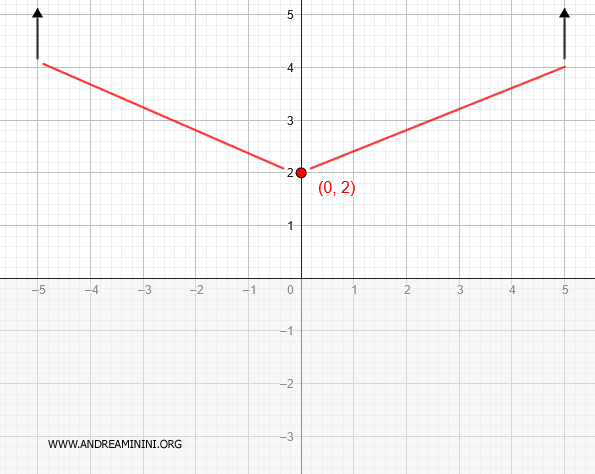
Punti di minimo e massimo

I punti di minimo e massimo si trovano nei punti stazionari ossia nei punti in cui la derivata prima si annulla

$$f'(x) = 0$$

$$e^x - e^{-x} = 0$$

$$e^x = e^{-x}$$

Per la proprietà invariantiva delle equazioni applico il logaritmo naturale a entrambi i membri.

$$\log e^x = \log e^{-x}$$

Il logaritmo e l'esponenziale sono l'una la funzione inversa dell'altra e si eliminano reciprocamente

$$x = -x$$

$$2x = 0$$

$$2x \cdot \frac{1}{2} = 0 \cdot \frac{1}{2}$$

$$x = 0$$

Nel punto x = 0 c'è un punto stazionario.

Si tratta di un punto di minimo locale perché la funzione è decrescente a sinistra di x=0 e crescente a destra di x=0.

In x=0 la funzione f(x) assume il valore y=2

$$f(x) = e^x + e^{-x}$$

$$f(0) = e^0 + e^{-0} = 1 + 1 = 2$$

Pertanto, la funzione ha un minimo locale nel punto (x;y)=(0;2)

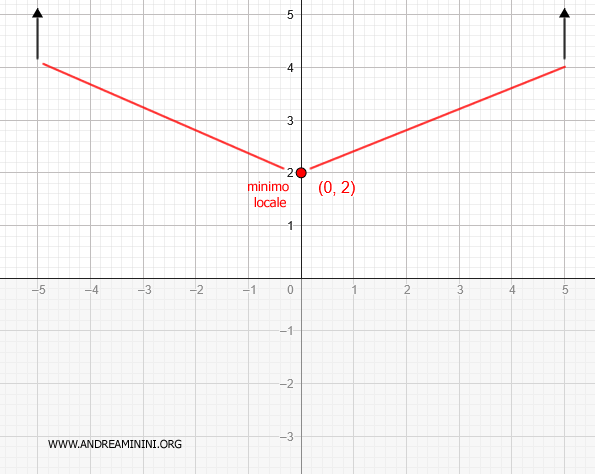
Concavità e convessità

Per studiare la concavità e la convessità della funzione studio la derivata seconda

Scelgo la funzione nell'espressione equivalente f(x)=e^x-e^-x perché mi semplifica i passaggi

$$f''(x) = D_x[ e^x - e^{-x} ]$$

$$f''(x) = D_x[ e^x] - D_x[ e^{-x} ]$$

$$f''(x) = e^x - ( e^{-x} \cdot -1)$$

$$f''(x) = e^x + e^{-x}$$

$$f''(x) = e^x + \frac{1}{e^x}$$

$$f''(x) = \frac{e^x \cdot e^x + 1}{e^x}$$

$$f''(x) = \frac{e^{2x} + 1}{e^x}$$

La derivata seconda f''(x)>0 è sempre positiva.

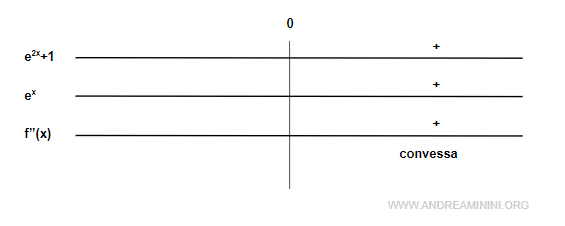
Quindi, la funzione f(x) è convessa in ogni punto del suo dominio D_f.

Questa informazione completa la costruzione del grafico della funzione.

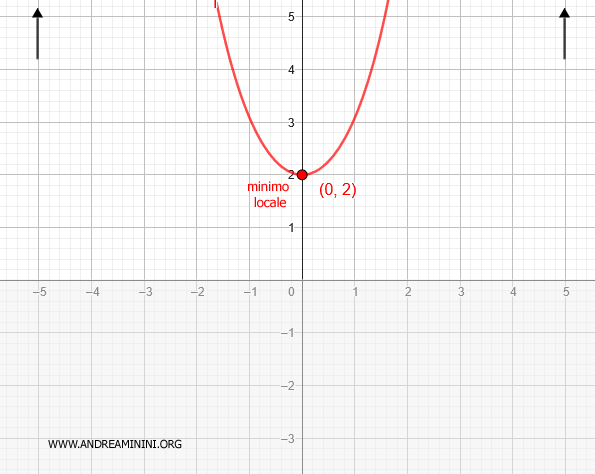
E così via.