Esercizio studio della funzione 5
Devo studiare la funzione e costruire il suo grafico
$$ f(x) = \frac{x}{1-x} $$
Si tratta di una funzione fratta.
Punti indefiniti
Per prima cosa cerco i punti in cui la funzione è indefinita.
$$ 1-x = 0 $$
$$ 1-x+x = 0+x $$
$$ x=1 $$
La funzione non è definita nel punto x=1 perché in questo punti si annulla il denominatore della frazione e la divisione per zero è un'operazione impossibile.
Dominio della funzione
La funzione è definita per tutti i numeri reali ad eccezione del punto x=1
$$ D_f = (- \infty, 1) \cup (1, \infty) $$
Intercette con gli assi
In x=0 la funzione assume il valore y=0
$$ f(0) = \frac{0}{1-0} = 0 $$
Pertanto, la funzione passa per l'origine degli assi O=(0;0)
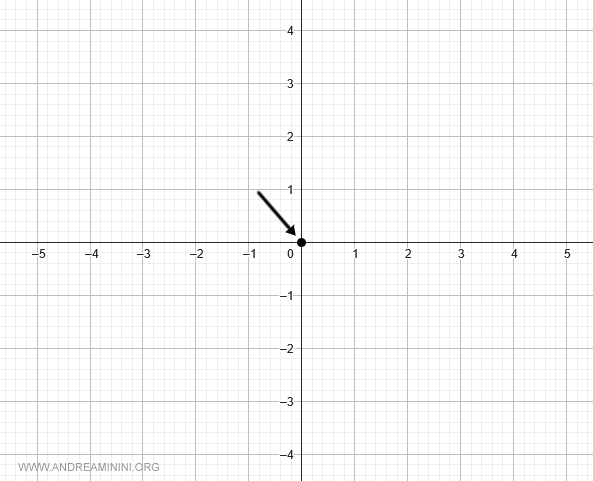
Studio del segno
Procedo con lo studio del segno della funzione
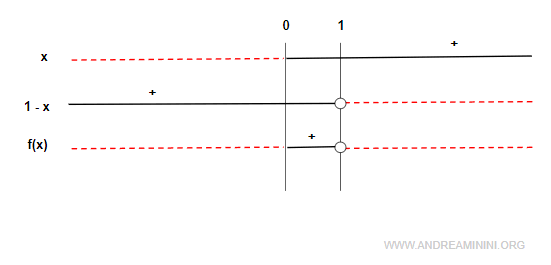
Nel suo dominio la funzione f(x) è positiva nell'intervallo (0,1), nulla in x=0 e negativa altrove.
Utilizzo le informazioni fin qui raccolte per delimitare le zone di interesse sul piano cartesiano.
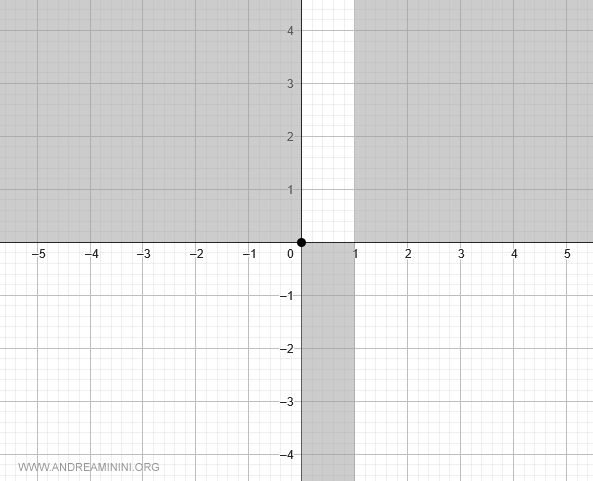
Asintoti orizzontali
Studio il comportamento della funzione tramite il limite che tende a più infinito
$$ \lim_{x \rightarrow + \infty} \frac{x}{1-x} = \frac{\infty}{-\infty} $$
Il limite è una forma indefinita del tipo ∞/∞. Quindi, per risolverla posso usare il teorema di De L'Hopital.
$$ \lim_{x \rightarrow + \infty} \frac{D[x]}{D[1-x]} = \frac{1}{-1} = -1 $$
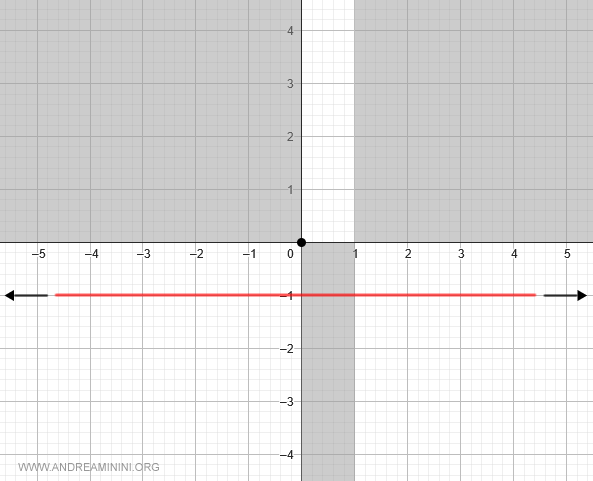
Per x→∞ la funzione tende a y=-1
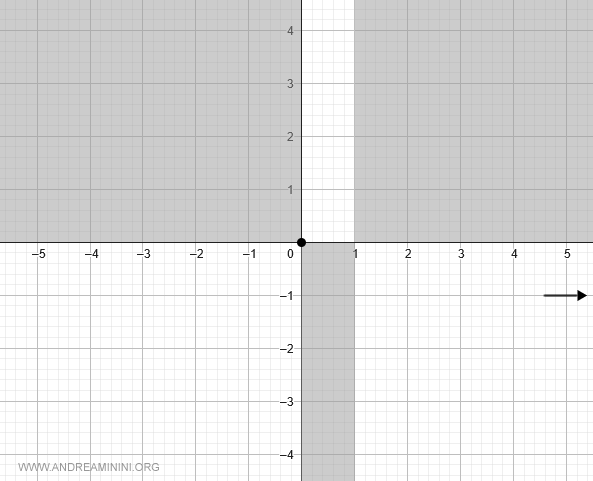
Ora studio il comportamento della funzione facendo tendere il limite a meno infinito
$$ \lim_{x \rightarrow - \infty} \frac{x}{1-x} = \frac{-\infty}{\infty} $$
Anche in questo caso il limite è una forma indeterminata del tipo ∞/∞ e per risolverla ricorro al teorema di De L'Hopital.
$$ \lim_{x \rightarrow - \infty} \frac{D[x]}{D[1-x]} = \frac{1}{-1} = -1 $$
Il limite della funzione per x→∞ è y=-1
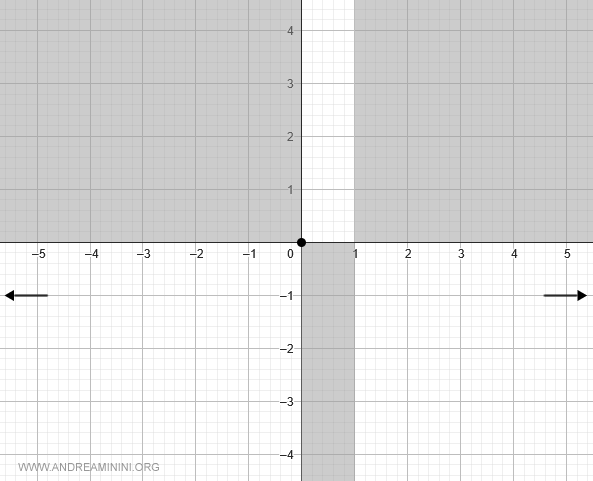
Poiché i due limiti a destra e a sinistra coincidono, in y=-1 la funzione ha un asintoto orizzontale.
Asintoti verticali
Gli asintoti verticali si trovano nei punti in cui la funzione non è definita. In questo caso la funzione non è definita in x=1.
Il limite della funzione per x che tende a 1 da destra (1+) è meno infinito
$$ \lim_{x \rightarrow 1^+} \frac{x}{1-x} = -\infty $$
Aggiungo la tendenza sul grafico
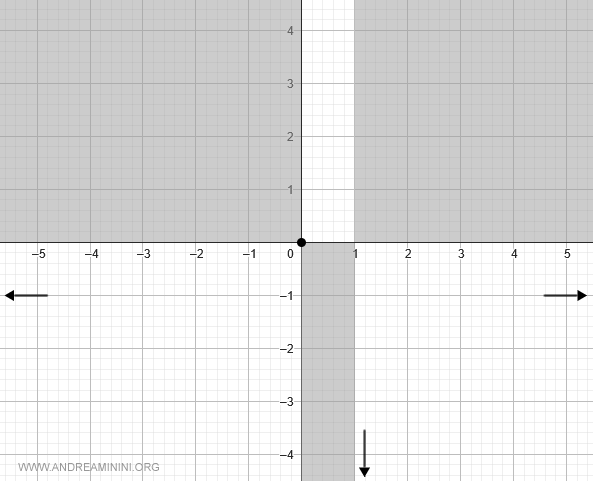
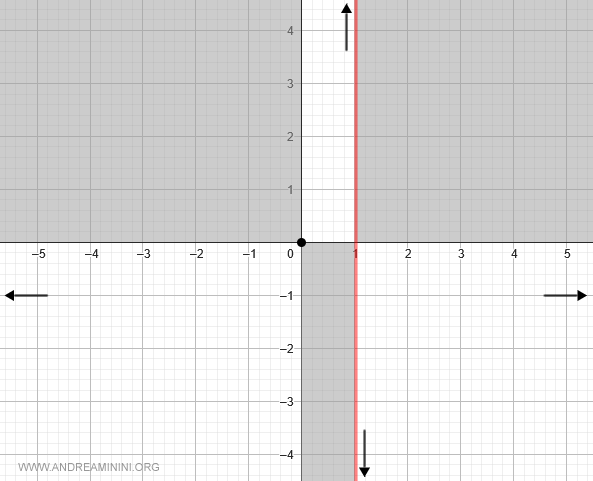
Il limite della funzione per x che tende a 1 da sinistra (1-) è più infinito
$$ \lim_{x \rightarrow 1^-} \frac{x}{1-x} = + \infty $$
Aggiungo la tendenza sul grafico
Crescenza e decrescenza
Per studiare la crescenza e la decrescenza devo calcolare la derivata prima della funzione
$$ f'(x) = D[ \frac{x}{1-x} ] $$
Applico la regola di derivazione del rapporto di due funzioni.
Nota. La derivata di una frazione fratta è la differenza tra la derivata del numeratore moltiplicato per il denominatore, meno il numeratore moltiplicato per la derivata del denominatore, diviso il quadrato del denominatore.
$$ f'(x) = \frac{D[x] \cdot (1-x) - x \cdot D[1-x ]}{(1-x)^2} $$
$$ f'(x) = \frac{1 \cdot (1-x) - x \cdot (-1)}{(1-x)^2} $$
$$ f'(x) = \frac{1-x + x}{(1-x)^2} $$
Pertanto, la derivata prima della funzione è
$$ f'(x) = \frac{1}{(1-x)^2} $$
Studio il segno della derivata prima per capire in quale intervallo la funzione cresce o decresce.
Al numeratore della funzione c'è una costante positiva (1) mentre al denominatore un'espressione di 2° grado
L'espressione (1-x)2 è una parabola rivolta verso l'alto (a>0) con una sola radice x=1.
Nota. Sapendo che $$ (1-x)^2 = x^2-2x+1 $$ Il coefficiente del termine di grado maggiore è positivo (a>0). Quindi la parabola è rivolta verso l'alto. Ponendo a zero l'equazione x2-2x+1=0 ottengo una sola soluzione. $$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$ $$ x = \frac{-(-2) \pm \sqrt{(-2)^2-4(1)(1)}}{2(1)} $$ $$ x = \frac{2 \pm \sqrt{4-4}}{2} $$ $$ x = \frac{2 \pm \sqrt{0}}{2} $$ $$ x = \frac{2}{2} = 1 $$
Pertanto, la derivata prima è sempre positiva f'(x)>0 in tutto il dominio Df della funzione.
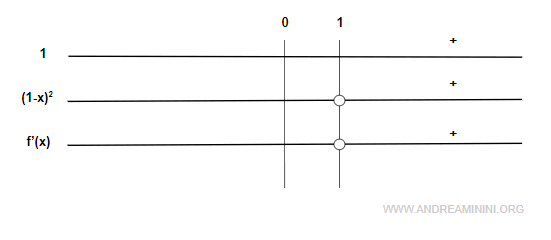
La derivata prima f'(x) è sempre crescente nel dominio.
Questo vuol dire che la funzione f(x) è sempre crescente in ogni punto del dominio.
Non essendoci radici f'(x)=0, non esistono punti di minimo o punti di massimo locali nella funzione.
Grazie a queste informazioni posso aggiornare il grafico della funzione.
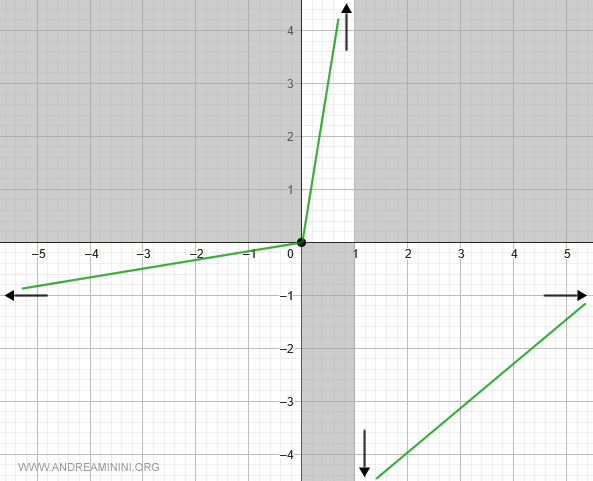
Concavità e convessità
Per capire la concavità e la convessità della funzione calcolo la derivata seconda della funzione
$$ f''(x) = D[ \frac{1}{(1-x)^2} ] $$
$$ f''(x) = \frac{D[1] \cdot (1-x)^2 - 1 \cdot D[(1-x)^2}{[(1-x)^2]^2} $$
$$ f''(x) = \frac{0 \cdot (1-x)^2 - 1 \cdot 2 \cdot (1-x) \cdot (-1)}{(1-x)^4} $$
$$ f''(x) = \frac{ 2 \cdot (1-x)}{(1-x)^4} $$
$$ f''(x) = \frac{ 2 }{(1-x)^3} $$
Poi studio il segno della derivata seconda
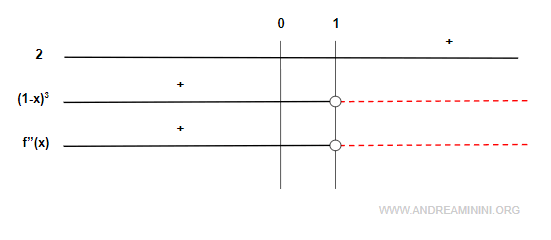
Lo studio del segno mi definisce le ultime informazioni utili per costruire il grafico.
- La derivata seconda è positiva f''(x)>0 nell'intervallo (-∞,1). Pertanto, in questo tratto la funzione f(x) è convessa.
- La derivata seconda è negativa f''(x)>0 nell'intervallo (1,∞). Pertanto, in questo tratto la funzione f(x) è concava.
Il grafico della funzione è il seguente
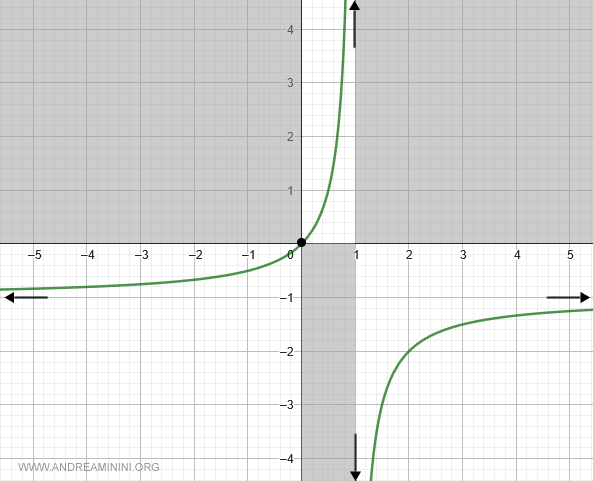
E così via.
