Problema di fisica 1

Conviene più spingere o tirare una cassa?

Per rispondere a questa domanda devo considerare la massa, le forze di coesione dell'attrito statico e dinamico che si oppongono allo spostamento della cassa, la forza esercitata per spostarla, la forza di gravità (g=-9.8 ms^-2).

I dati del problema

• La massa della cassa è m=2 kg
• Il coefficiente di attrito statico è 0.5 e di attrito dinamico 0.25
• Caso 1: provo a spingere la cassa con una forza F pari a 20 N (newton) e un angolo di 120° rispetto alla normale.
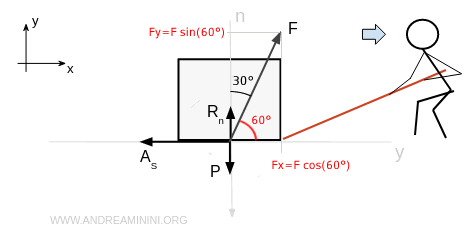
• Caso 2: provo a tirare la cassa con una forza F pari a 20 N (newton) e un angolo di 30° rispetto alla normale.

Nota. La forza per tirare o spingere la cassa è sempre la stessa F=20 N. Tra i due casi cambia soprattutto l'angolo rispetto alla normale tramite il quale la cassa viene tirata.

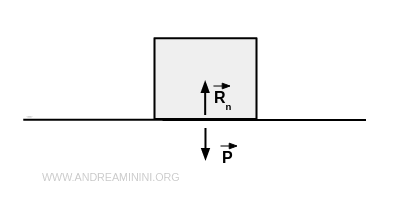
Quando la cassa è ferma (stato di quiete) la reazione vincolare R è uguale alla forza peso P.

$$ \vec{R} = \vec(P) $$

Supponendo che il piano riesca a sopportare il peso della cassa, le due forze sono uguali e contrapposte F+P=0

Caso 1: la persona spinge la cassa

Spingo la cassa con un vettore forza F e un angolo di α = 120° gradi rispetto alla reazione vincolare normale.

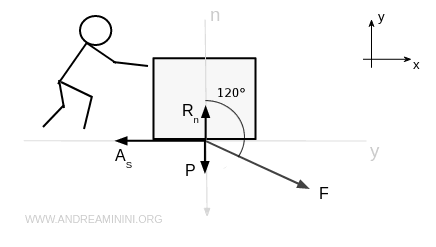
Allo spostamento si oppone la forza di coesione A_s (attrito statico) tra la cassa e il pavimento.

La cassa resta ferma fin quando la somma vettoriale si annulla.

$$ \vec{R} + \vec(P) + \vec{F} + \vec{A_s} = 0 $$

Proietto le grandezze vettoriali sull'asse normale (y) e tangente (x).

Il risultato è un sistema di due equazioni:

$$ \begin{cases} F_x - A_s = 0 \ \ \ \ (asse \ x) \\ \\ R_n - P - F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

In questo caso la forza F ha due componenti

• La forza tangenziale F_x sposta la cassa verso destra
• La forza normale F_y ha verso opposto rispetto alla reazione normale Rn. Per questa ragione ha segno meno.

Nota. La forza di attrito A non ha una componente normale. Quindi, appare solo la proiezionie sull'equazione tangenziale (asse x)

Per spostare la cassa sul piano la componente Fx deve essere superiore all'attrito statico

$$ \begin{cases} F_x - A_s \color{red}> 0 \ \ \ \ (asse \ x) \\ \\ R_n - P - F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

Poiché il corpo è in stato di quiete devo considerare il coefficiente di attrito statico μ_s = 0.5

Quindi la forza di attrito statico è A_s=μ_sRn

$$ \begin{cases} F_x - \color{red}{A_s} > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P - F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - \mu_s \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P - F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P - F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

A questo punto per capire se la cassa si sposta sul piano devo calcolare il valore della reazione normale R_n

Per ottenerla lavoro sulla seconda equazione del sistema

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = P + F_y \ \ \ \ (asse \ y) \end{cases} $$

Sapendo che il modulo della forza peso P è il prodotto tra la massa e la gravità P=m·g=2 kg·9.8 ms^-2=18.4 N

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = \color{red}P + F_y \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = mg + F_y \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 + F_y \ \ \ \ (asse \ y) \end{cases} $$

Poiché la forza F è presente sia sulla normale (y) che sulla tangenziale (x) devo calcolare le due componenti.

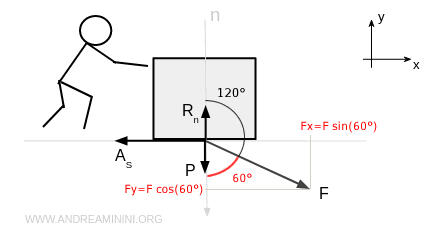
Quindi le componenti Fx e Fy della forza sono

$$ F_x =| \ \sin ( 60° ) \cdot 20 N \ | \ = \ | \ 0.87 \cdot 20 \ | \ = 17.4 N $$

$$ F_y = \ | \ \cos ( 60° ) \cdot 20 N \ | \ = \ | \ 0.5 \cdot 20 \ | \ = 10 N $$

Questo mi permette di calcolare la reazione normale R_n nel sistema

$$ \begin{cases} \color{red}{F_x} - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 + \color{red}{F_y} \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 + 10 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 28.4 \ \ \ \ (asse \ y) \end{cases} $$

Una volta nota la reazione la reazione vincolare normale R_n=28.4 posso calcolare l'attrito statico

$$ \begin{cases} 17.4 - 0.5 \cdot \color{red}{R_n} > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 28.4 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 0.5 \cdot 28.4 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 28.4 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 14.2 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 28.4 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 3.2 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 28.4 \ \ \ \ (asse \ y) \end{cases} $$

La prima equazione è soddisfatta. Pertanto, la cassa si sposta.

Il modulo della reazione vincolare considerando le componenti x e y è

$$ R = \sqrt{ R_n^2 + A_s^2 } = \sqrt{28.4^2 + 14.2^2} = 31.75 \ N $$

Caso 2: la persona tira la cassa

Tiro la cassa con un vettore forza F e un angolo di α = 30° gradi rispetto alla reazione vincolare normale.

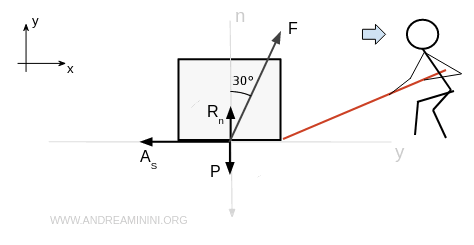
Lo spostamento della cassa è ostacolato dalla forza di coesione A_s (attrito statico) tra la cassa e il pavimento.

La cassa resta in stato di quiete (ferma) finché vettoriale si annulla.

$$ \vec{R} + \vec(P) + \vec{F} + \vec{A_s} = 0 $$

La proiezione delle grandezze vettoriali sull'asse normale (y) e tangente (x) genera un sistema di due equazioni.

$$ \begin{cases} F_x - A_s = 0 \ \ \ \ (asse \ x) \\ \\ R_n - P + F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

In questo caso la forza F ha due componenti

• La forza tangenziale F_x sposta la cassa verso destra
• La forza normale F_y ha lo stesso verso rispetto alla reazione normale Rn. Pertanto, in questo caso F_y ha segno più.

Nota. La forza di attrito A non ha una componente normale. Quindi, appare solo la proiezionie sull'equazione tangenziale (asse x)

La cassa inizia a muoversi verso destra se la componente Fx è superiore all'attrito statico A_s

$$ \begin{cases} F_x - A_s \color{red}> 0 \ \ \ \ (asse \ x) \\ \\ R_n - P + F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

La forza di attrito statico è A_s=μ_sRn

Essendo il corpo è in stato di quiete considero il coefficiente di attrito statico μ_s = 0.5

$$ \begin{cases} F_x - \color{red}{A_s} > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P + F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - \mu_s \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P + F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n - P + F_y = 0 \ \ \ \ (asse \ y) \end{cases} $$

Per capire se la cassa si sposta sul piano calcolo il valore della reazione normale R_n nella seconda equazione del sistema

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = P - F_y \ \ \ \ (asse \ y) \end{cases} $$

Il modulo della forza peso P è il prodotto tra la massa e la gravità P=m·g=2 kg·9.8 ms^-2=18.4 N

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = \color{red}P - F_y \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = mg - F_y \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} F_x - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 - F_y \ \ \ \ (asse \ y) \end{cases} $$

A questo punto calcolo le componenti della forza F sulla normale (y) e sulla tangenziale (x)

Quindi le componenti F_x e F_y della forza sono

$$ F_x =| \ \cos( 60° ) \cdot 20 N \ | \ = \ | \ 0.50 \cdot 20 \ | \ = 10 N $$

$$ F_y = \ | \ \sin ( 60° ) \cdot 20 N \ | \ = \ | \ 0.87 \cdot 20 \ | \ = 17.4 N $$

Questo mi permette di calcolare la reazione normale R_n nel sistema

$$ \begin{cases} \color{red}{F_x} - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 - \color{red}{F_y} \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 10 - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 18.4 - 17.4 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 10 - 0.5 \cdot R_n > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 1 \ \ \ \ (asse \ y) \end{cases} $$

Una volta nota la reazione la reazione vincolare normale R_n=1 completo il calcolo dell'attrito statico

$$ \begin{cases} 17.4 - 0.5 \cdot \color{red}{R_n} > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 1 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 0.5 \cdot 1 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 1 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 17.4 - 0.5 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 1 \ \ \ \ (asse \ y) \end{cases} $$

$$ \begin{cases} 16.9 > 0 \ \ \ \ (asse \ x) \\ \\ R_n = 1 \ \ \ \ (asse \ y) \end{cases} $$

La prima equazione è soddisfatta. Pertanto, la cassa si sposta.

Il modulo della reazione vincolare considerando le componenti x e y è

$$ R = \sqrt{ R_n^2 + A_s^2 } = \sqrt{1^2 + 0.5^2} = 1.1 \ N $$

E' quindi notevolmente più basso rispetto al primo caso, perché questa volta la componente F_y ha lo stesso verso della reazione vincolare sulla normale R_n.

In conclusione, tirando la cassa si fatica di meno.

E così via