Esercizi sull'attrito statico
Esercizi svolti e spiegati passo passo per affrontare problemi di fisica sull'attrito statico.
Esercizio 1
Attrito statico e inclinazione del piano: esercizi con cassa in equilibrio
Una cassa di 80 kg si trova su un piano inclinato di 20° ed è in equilibrio, non si muove, qual è la forza di attrito statico? Se la cassa comincia a muoversi a 30°, qual è il coefficiente di attrito statico?
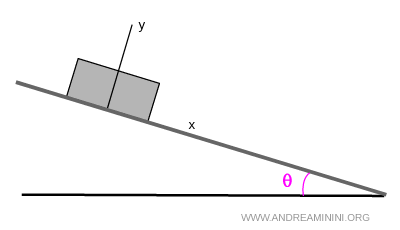
Prendo come sistema di riferimento il piano come asse x e la perpendicolare al piano come asse y.
Per prima cosa calcolo il modulo della forza peso del corpo.
$$ P = m \cdot g $$
Dove $ m = 80 \ kg $ è la massa del corpo e $ g = 9,81 \ N/kg $ è l'accerazione di gravità terrestre.
$$ P = 80 \ kg \cdot 9,81 \ N/kg $$
$$ P = 80 \ kg \cdot 9,81 \ N/kg $$
$$ P = 785 \ N $$
Il vettore della forza peso P è orientato verso il centro della Terra.
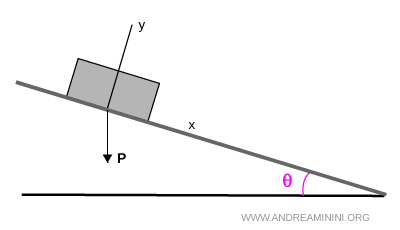
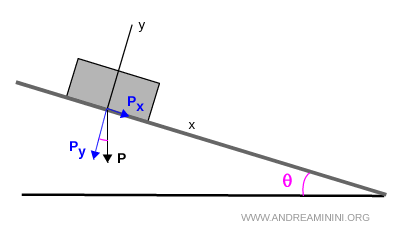
Ora scompongo il modulo della forza peso proiettandola sugli assi di riferimenti.
$$ \begin{cases}
P_x = P \cdot \sin 20° \\ \\
P_y = P \cdot \cos 20° \end{cases} $$
$$ \begin{cases}
P_x = 785 \ N \cdot 0,34 \\ \\
P_y = 785 \ N \cdot 0,94 \end{cases} $$
$$ \begin{cases}
P_x = 277 \ N \\ \\
P_y = 769 \ N \end{cases} $$
Quindi, le componenti della forza peso sugli assi x e y sono Px e Py.
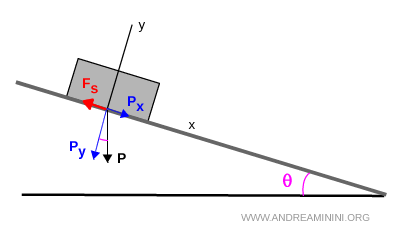
La forza di attrito statico $ F_s $ è la forza che si oppone allo scivolamento della cassa sul piano.
$$ F_s = P_x = 277 \ N $$
Quindi, la forza di attrito statico è $ F_s = 277 \ N $
La seconda domanda mi chiede di trovare il coefficiente di attrito sapendo $ \mu_s $ sapendo che la cassa comincia a muoversi quando il piano è inclinato di 30°.
La forza di attrito statico massimo è
$$ F_{s,max} = \mu_s \cdot F_N $$
Tenendo a mente questa formula, ricalcolo la forza normale quando il piano è inclinato di 30°.
$$ \begin{cases}
P_x = P \cdot \sin 30° \\ \\
P_y = P \cdot \cos 30° \end{cases} $$
$$ \begin{cases}
P_x = 785 \ N \cdot 0,5 \\ \\
P_y = 785 \ N \cdot 0,87 \end{cases} $$
$$ \begin{cases}
P_x = 393 \ N \\ \\
P_y = 683 \ N \end{cases} $$
La forza normale $ F_N $ è la forza perpendicolare al piano, di reazione vincolare, che si oppone alla forza peso.
$$ F_N = P_y = 683 \ N $$
La forza di attrito statico è invece
$$ F_s = P_x = 393 \ N $$
Poiché la cassa comincia a muoversi, questa è anche la forza di attrito statico massimo.
$$ F_{s,max} = 393 \ N $$
A questo punto, torno alla formula dell'attrito statico max e sostituisco i valori che ho appena trovato.
$$ F_{s,max} = \mu_s \cdot F_N $$
$$ 393 \ N = \mu_s \cdot 683 \ N $$
$$ \mu_s = \frac{ 393 \ N }{ 683 \ N} $$
$$ \mu_s = 0,58 $$
Il coefficiente di attrito statico è 0,58.
Se il piano ha una inclinazione di 10° quale è il coefficiente di attrito statico minimo che impedisce alla cassa di scivolare?
In questo caso si parte dal fatto che il piano è inclinato di 10°.
Devo calcolare il coefficiente di attrito statico minimo che mantiene ferma la cassa a questa angolazione.
Sapendo che la forza di attrito statico massimo è
$$ F_{s,max} = \mu_s \cdot F_N $$
Calcolo la forza di attrito statico e la forza normale della cassa quando il piano è inclinato di 10°
$$ \begin{cases}
P_x = P \cdot \sin 10° \\ \\
P_y = P \cdot \cos 10° \end{cases} $$
$$ \begin{cases}
P_x = 785 \ N \cdot 0,17 \\ \\
P_y = 785 \ N \cdot 0,98 \end{cases} $$
$$ \begin{cases}
P_x = 136 \ N \\ \\
P_y = 773 \ N \end{cases} $$
Dove $ F_s= 136 \ N $ e $ F_N = 773 \ N $
Per ipotesi considero $ F_s = F_{s,max} $ e sostituisco i dati nella formula della forza di attrito statico massimo.
$$ F_{s,max} = \mu_s \cdot F_N $$
$$ 136 \ N = \mu_s \cdot 773 \ N $$
$$ \mu = \frac{ 136 \ N }{773 \ N} $$
$$ \mu = 0,18 $$
Questo significa che la cassa comincia a muoversi quando il coefficiente di attrito è $ \mu = 0,18 $ sul piano inclinato di 10°.
Quindi, la cassa resta ferma per coefficienti di attrito statico maggiori di $ \mu > 0,18 $.
Se la cassa inizia a scivolare quando il coefficiente di attrito statico massimo è 0,4 qual è l'inclinazione massima del piano?
Per rispondere a questa domanda considero la formula dell'attrito statico massimo.
$$ F_{s,max} = \mu_s \cdot F_N $$
Poiché conosco già il coefficiente di attrito posso sostituirlo nella formula.
$$ F_{s,max} = 0,4 \cdot F_N $$
Calcolo la forza di attrito statico e la forza normale, considerando l'angolazione $ \theta $ del piano come una incognita.
$$ \begin{cases}
P_x = P \cdot \sin \theta \\ \\
P_y = P \cdot \cos \theta \end{cases} $$
$$ \begin{cases}
P_x = 785 \ N \cdot \sin \theta \\ \\
P_y = 785 \ N \cdot \cos \theta \end{cases} $$
Dove $ F_s= 785 \ N \cdot \sin \theta \ N $ e $ F_N = 785 \ N \cdot \cos \theta \ N $
Poi sostituisco i dati appena trovati nella formula dell'attrito statico.
$$ F_{s,max} = 0,4 \cdot F_N $$
$$ 785 \ N \cdot \sin \theta = 0,4 \cdot ( 785 \ N \cdot \cos \theta ) $$
$$ 785 \ N \cdot \sin \theta = 314 \ N \cdot \cos \theta $$
$$ \frac{ \sin \theta }{ \cos \theta } = \frac{ 314 \ N }{ 785 \ N } $$
$$ \frac{ \sin \theta }{ \cos \theta } = 0,4 $$
Sapendo che $ \frac{ \sin \theta }{ \cos \theta } = \tan \theta $
$$ \tan \theta = 0,4 $$
A questo punto calcolo l'arcotangente di 0,4 e ottengo l'angolo $ \theta $ che cercavo
$$ \theta = \tan^{-1} (0,4 ) = 21,8° $$
Quindi, la cassa comincia a muoversi quando il piano raggiunge un angolo di 21,8°.
Esercizio 2
Una cassa di massa $ m = 4,8 \cdot 10^2 kg $ è ferma su una rampa inclinata di 15°. Calcola la forza normale e la forza di attrito statico.
Scelgo un sistema di riferimento inclinato: l’asse $x$ parallelo al piano inclinato e l’asse $y$ perpendicolare al piano. In questo modo la forza peso si scompone più facilmente e i calcoli si semplificano.
Calcolo la forza peso della cassa
$$ P = m \cdot g $$
Dove $ m = 4,8 \cdot 10^2 kg $ è la massa della cassa e $ g=9,81 \ N/kg $ è l'accelerazione terrestre che spinge ogni corpo verso il centro della Terra.
$$ P = 4,8 \cdot 10^2 kg \cdot 9,81 \ N/kg $$
$$ P = 47,1 \cdot 10^2 \ N $$
$$ P = 4,71 \cdot 10^3 \ N $$
Poi proietto la forza peso sugli assi x e y del sistema di riferimento.
$$ \begin{cases} P_x = P \sin 15° \\ \\ P_y = P \cos 15° \end{cases} $$
$$ \begin{cases} P_x = 4,71 \cdot 10^3 \ N \cdot \sin 15° \\ \\ P_y = 4,71 \cdot 10^3 \ N \cdot \cos 15° \end{cases} $$
Per semplicità utilizzo dei valori approssimati a due cifre decimali del seno e del coseno.
$$ \begin{cases} P_x = 4,71 \cdot 10^3 \ N \cdot 0,26 \\ \\ P_y = 4,71 \cdot 10^3 \ N \cdot 0,97 \end{cases} $$
$$ \begin{cases} P_x = 1,22 \cdot 10^3 \ N \\ \\ P_y = 4,55 \cdot 10^3 \ N \end{cases} $$
La forza normale bilancia la componente perpendicolare della forza peso:
$$ F_N = P_y = 4,55 \cdot 10^3 \ N $$
Poiché la cassa è ferma, la forza di attrito statico bilancia la componente parallela al piano:
$$ F_s = P_x = 1,22 \cdot 10^3 \ N $$
L’esercizio è completato. La forza normale esercitata dal piano sulla cassa è di $4,55 \cdot 10^3 , \text{N}$, mentre la forza di attrito statico che impedisce lo scivolamento è di $1,22 \cdot 10^3 , \text{N}$.
Esercizio 3
Esercizi sulla forza di attrito in presenza di una molla
Un oggetto di massa 20 kg è fermo su un piano orizzontale, collegato a una parete tramite una molla con costante elastica $k = 200 \ \text{N/m}$. La molla risulta allungata di 10 cm rispetto alla sua lunghezza a riposo. Qual è la forza di attrito statico che mantiene l’oggetto in equilibrio?
Per risolvere questo problema devo usare la formule della forza elastica.
Poiché lavoro sul piano orizzontale, utilizzo direttamente il modulo della forza.
$$ F_e = k \cdot x $$
Dove $ k = 200 \ \text{N/m} $ è la costante elastica e $ x=10 \ cm $ è l'allungamento della molla.
$$ F_e = 200 \ \text{N/m} \cdot 10 \ cm $$
Trasformo i centimetri in metri
$$ F_e = 200 \ \text{N/m} \cdot 0,10 \ m $$
$$ F_e = 20 \ N $$
La forza di attrito statico $ F_s $ eguaglia la forza elastica, poiché l'oggetto è in equilibrio
$$ F_s = F_e $$
Quindi, la forza di attrito statico che mantiene in equilibrio l'oggetto è
$$ F_s = 20 \ N $$
Qual è la forza di attrito statica massima?
Se la molla può essere allungata fino a 30 cm prima che l'oggetto cominci a muoversi, quale è la forza di attrito statica massima?
Riprendo la formula della forza elastica
$$ F_e = k \cdot x $$
$$ F_e = 200 \ \text{N/m} \cdot x $$
In questo caso considero un allungamento della molla di 30 cm rispetto alla sua condizione di riposo.
$$ F_e = 200 \ \text{N/m} \cdot 30 \ cm $$
Converto i centimetri in metri per semplificare la formula.
$$ F_e = 200 \ \text{N/m} \cdot 0,30 \ m $$
$$ F_e = 60 \ N $$
Sapendo che fino a 30 cm di allungamento il corpo resta in quiete, deduco che la forza di attrito statico massimo sia uguale alla forza elastica
$$ F_s = F_e = 60 \ N $$
Quindi, la forza di attrito statico massimo è $ F_{s,max} = 60 \ N $
Qual è il coefficiente di attrito statico del piano?
Quanto vale il coefficiente di attrito statico del piano?
Per rispondere a questa domanda, utilizzo la formula della forza di attrito statico massimo:
$$ F_{s,max} = \mu_s \cdot F_N $$
So già che la forza di attrito statico massimo è $ F_{s,max} = 60 \ N $
$$ 60 \ N = \mu_s \cdot F_N $$
La forza normale è la reazione vincolare del piano al corpo ed è perpendicolare al piano. Quindi, si oppone alla forza peso dell'oggetto.
$$ P = m \cdot g $$
Dove $ m = 20 \ kg $ è la massa dell'oggetto mentre $ g=9,81 \ N /kg $ è la forza di gravità terrestre.
$$ P = 20 \ kg \cdot 9,81 \ kg/N $$
$$ P = 196,2 \ N $$
La forza normale è uguale alla forza peso poiché impedisce al corpo di cadere.
$$ F_N = P = 196,2 \ N $$
Una volta nota la forza normale, posso tornare alla formula della forza di attrito statico e calcolare il coefficiente di attrito statico.
$$ 60 \ N = \mu_s \cdot F_N $$
$$ 60 \ N = \mu_s \cdot 196,2 \ N $$
$$ \mu_s = \frac{ 60 \ N }{196,2 \ N} \approx 0,31 $$
Pertanto, il coefficiente di attrito statico del piano è $ \mu_s \approx 0,31 $.
E così via.
