Esercizi sulle tensioni in una fune
Alcuni esercizi svolti e spiegati passo passo che coinvolgono la tensione di una fune.
Esercizio 1
Tensione in due funi simmetriche che sostengono un corpo appeso
Un corpo di massa 10,0 kg è appeso al soffitto in equilibrio mediante due funi che formano un angolo di 30° rispetto alla verticale, qual è la la tensione in ciascuna delle funi.
Per risolvere questo problema, userò le condizioni di equilibrio statico: il corpo è fermo, quindi la somma delle forze in ogni direzione deve essere zero.
Il corpo ha una massa $m = 10{,}0,\text{kg} $ e le due funi formano un angolo $ \theta = 30^\circ $ rispetto alla verticale.
Le funi sono simmetriche, quindi la tensione è la stessa in entrambe $ T_1 = T_2 $.
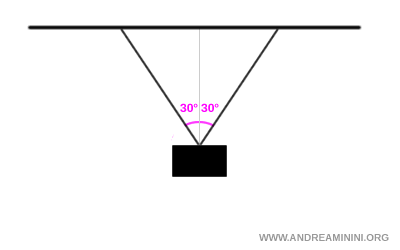
Scelgo come sistema di riferimento la verticale come asse $ y $ e la retta perpendicolare all'estremità della fune come asse $ x $.
Le tensioni sono i vettori sulle funi mentre la forza peso è il vettore che spinge il corpo verso il basso.
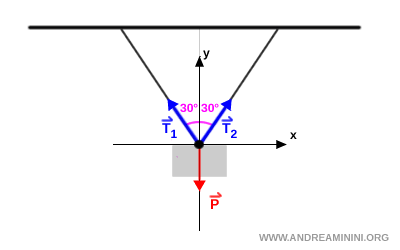
Poiché non viene detto nulla sulla massa della fune, presumo che non sia significativa.
I vettori $ \vec{ T }_1 $ e $ \vec{ T }_2 $ non si trovano sugli assi, quindi uso il metodo della proiezione per scomporli.
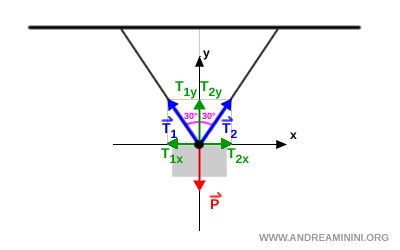
In condizioni di equilibrio la somma delle forze sull'asse x e sull'asse y è nulla.
Quindi, la somma delle componenti verticali delle tensioni deve equilibrare il peso:
$$ \begin{cases} T_{1y} + T_{2y} - P = 0 \\ \\ -T_{1x} + T_{2x} = 0 \end{cases} $$
$$ \begin{cases} T_{1y} + T_{2y} - P = 0 \\ \\ T_{1x} = T_{2x} \end{cases} $$
Calcolo la forza peso del corpo.
$$ P = mg = 10,0 \cdot 9,8 = 98 \ N $$
Poi sostituisco la forza peso nel sistema.
$$ \begin{cases} T_{1y} + T_{2y} - 98 \ N = 0 \\ \\ T_{1x} = T_{2x} \end{cases} $$
$$ \begin{cases} T_{1y} + T_{2y} = 98 \ N \\ \\ T_{1x} = T_{2x} \end{cases} $$
Sostituisco $ T_{1y} = T_1 \cdot \cos 30° $ e $ T_{2y} = T_2 \cdot \cos 30° $
$$ \begin{cases} T_1 \cdot \cos 30° + T_2 \cdot \cos 30° = 98 \ N \\ \\ T_{1x} = T_{2x} \end{cases} $$
$$ \begin{cases} (T_1 + T_2 ) \cdot \cos 30° = 98 \ N \\ \\ T_{1x} = T_{2x} \end{cases} $$
$$ \begin{cases} (T_1 + T_2 ) = \frac{ 98 \ N }{ \cos 30° } \\ \\ T_{1x} = T_{2x} \end{cases} $$
Sapendo che il coseno di 30° vale approssimativamente $ \cos 30° = 0,866 $
$$ \begin{cases} (T_1 + T_2 ) = \frac{ 98 \ N }{ 0.866 } \\ \\ T_{1x} = T_{2x} \end{cases} $$
$$ \begin{cases} (T_1 + T_2 ) = 113,16 \ N \\ \\ T_{1x} = T_{2x} \end{cases} $$
La somma delle due tensioni è uguale a $ T_{1y}+T_{2y} = 113,16 N $ e poiché sono simmetriche, deduco che ciascuna tensione è pari alla metà della somma.
Sapendo che $ T_1 = T_2 $
$$ T_1 + T_2 = 113,16 \ N $$
$$ T_1 + T_1 = 113,16 \ N $$
$$ 2T_1 = 113,16 \ N $$
$$ T_1 = \frac{113,16}{2} \ N $$
$$ T_1 = 56,58 \ N $$
Di conseguenza anche $ T_2 = 56,58 \ N $
$$ T_1 + T_2 = 113,16 \ N $$
$$ 56,58 \ N + T_2 = 113,16 \ N $$
$$ T_2 = 113,16 \ N - 56,58 \ N $$
$$ T_2 = 56,58\ N $$
Pertanto, la tensione in ciascuna fune è $ T_1 = T_2 = 56,58 \ N $
Esercizio 2
Tensione di una fune in una carrucola con un corpo appeso e una molla
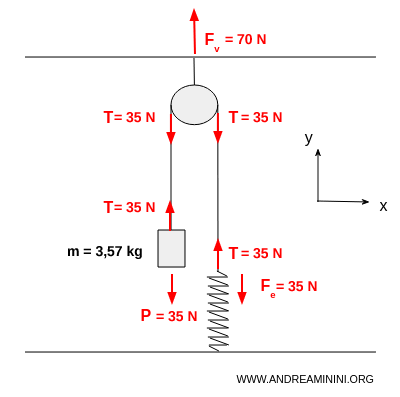
Una carrucola fissata al soffitto ha due estremità di una fune che scendono lateralmente. La prima estremità della fune è collegata a un peso di massa $ m $, la seconda estremità è collegata a una molla fissata al pavimento. Sapendo che la molla è in equilibrio con un allungamento $ x=25 cm $ e la costante elastica è $ k =140 \ N/m $, devo determinare la tensione $ T $ sulla fune, la massa $ m $ del corpo e la reazione vincolare $ F_v $ al soffitto.
Scelgo come sistema di riferimento gli assi cartesiani, ponendo l'asse y parallelo alle funi e l'asse x perpendicolare.
Ecco la rappresentazione grafica del problema e delle varie forze.
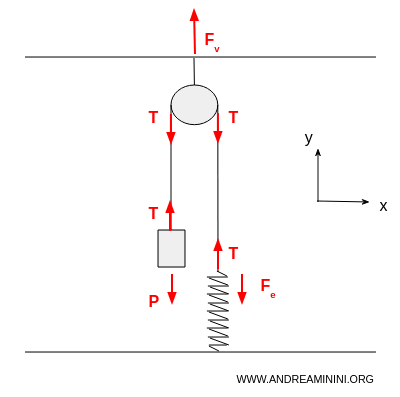
Tutte le forze agiscono verticalmente sull'asse y.
Quindi, le forze sono in equilibrio quando la loro somma vettoriale si annulla.
$$ \vec{F_v} - 2 \vec{T} + 2 \vec{T} - \vec{P} - \vec{F_e} = 0 $$
ossia
$$ \vec{F_v} - \vec{P} - \vec{F_e} = 0 $$
$$ \vec{F_v} = \vec{P} + \vec{F_e} $$
Il modulo della forza elastica $ F_e $ posso ottenerlo usando la legge di Hooke.
$$ F_e = k \cdot x $$
Dove l'allungamento della molla è $ x=25 \ cm $ e la costante elastica è $ k = 140 \ N/m $
$$ F_e = 140 \ N/m \cdot 25 \ cm $$
Trasformo i centimetri in metri
$$ F_e = 140 \ N/m \cdot 0,25 \ m $$
$$ F_e = 140 \ N \cdot 0,25 $$
$$ F_e = 35 \ N $$
La forza elastica sulla molla ha una intensità di 35 N.
Poiché la tensione $ T $ della fune compensa la forza elastica, deve avere anche la stessa intensità ossia lo stesso modulo
$$ T = F_e = 35 \ N $$
Quindi, anche la tensione sulla fune ha un'intensità di 35 N.
All'altra estremità della fune la tensione compensa anche la forza peso del corpo, quindi entrambe le forze hanno la stessa intensità.
$$ P = T = 35 \ N $$
Sapendo che la forza peso è $ P=mg $ dove $ m $ è la massa e $ g =9,81 \ N/kg $ è l'accelerazione di gravità terrestre.
$$ P = m \cdot g $$
In questo caso la forza peso è 35 N.
$$ 35 \ N = m \cdot 9,81 \ N/kg $$
Questo mi permette di ricavare la massa $ m $
$$ m = \frac{ 35 \ N }{ 9,81 \ N/kg } = 3,57 \ kg $$
Quindi, il corpo ha una massa di 3,57 kg.
Infine, per trovare la reazione vincolare al soffitto basta tornare all'equazione dell'equilibrio del sistema.
$$ \vec{F_v} = \vec{P} + \vec{F_e} $$
L'intensità (modulo) della reazione vincolare deve compensare la somma delle forze che agiscono nel verso opposto, ossia il peso e la forza elastica.
$$ F_v = P + F_e $$
In questo caso $ P = F_e = 35 \ N $
$$ F_v = 35 \ N + 35 \ N $$
$$ F_v = 70 \ N $$
La reazione vincolare è pari a 70 N, esattamente il doppio della forza peso.
E così via.
