Moto verticale di un corpo
Sulla Terra un corpo lasciato libero di cadere, senza considerare l'attrito con l'aria, si muove verso il basso con un'accelerazione costante di g=9.8 ms2.
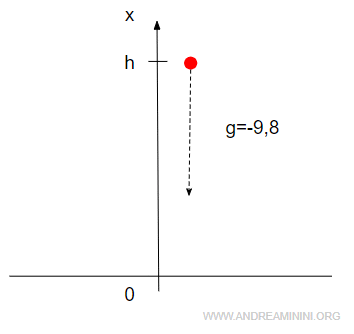
Si tratta di un moto rettilineo uniformemente accelerato.
La velocità
Se il corpo cade da un'altezza h=x0 e ha inizialmente una velocità nulla (v=0) nell'istante t0=0, allora la velocità del corpo è data dalla formula.
$$ v(t)=- gt $$
Il segno meno deriva dall'asse verticale. Per ipotesi ho fissato l'origine O alla superficie terrestre (h=0).
Durante la caduta la velocità aumenta.
Per conoscere la velocità del corpo in base allo spazio posso usare la relativa formula del moto uniformemente accelerato.
$$ v^2 = v_0^2 + 2a (x-x_0) $$
Quindi sostituendo le variabili ottengo
$$ v^2 = 0^2 + 2(-g) (x-h) $$
$$ v^2 = 2g (h-x) $$
$$ v = \sqrt{ 2g (h-x) } $$
E' la formula che mi permette di calcolare la velocità in funzione dello spazio percorso in caduta.
$$ v = \sqrt{ 2g (h-x) } $$
Il corpo raggiunge la velocità massima un istante prima di toccare il suolo (x=0).
Un esempio pratico
Un punto cade da un'altezza di 20 metri (h=20).
Al momento di toccare il suolo raggiunge la velocità massima di 19,7 metri al secondo.
$$ v = \sqrt{ 2g (h-x) } = \sqrt{ 2 \cdot 9.8 (20-0) } = 19,7 m/sec. $$
E così via.
La legge oraria
La legge oraria del moto uniformemente accelerato è
$$ x(t) = \frac{1}{2} a(t-t_0)^2+v_0(t-t_0)+x_0 $$
Sapendo che t0=0 e v0=0.
$$ x(t) = \frac{1}{2} a(t)^2+x_0 $$
Sostituisco x0 con l'altezza h,
$$ x(t) = \frac{1}{2} a(t)^2+h $$
Infine, sostituisco l'accelerazione (a) con quella gravitazionale (-g).
Ho così ottenuto la legge oraria di un punto in moto verticale ( caduta ).
$$ x(t) = h - \frac{1}{2} gt^2 $$
Da quest'ultima posso ricavare la formula del tempo di caduta fino al suolo.
$$ t=\sqrt{\frac{2 h}{g}} $$
Dimostrazione. $$ x(t) = h - \frac{1}{2} gt^2 \\ x(t) - h = - \frac{1}{2} gt^2 \\ \frac{2( x(t) - h)}{g} = - t^2 $$ al suolo x(t)=0 $$ \frac{2( 0 - h)}{g} = - t^2 \\ \frac{-2h}{g} = -t^2 \\ \frac{2 h}{g} = t^2 \\ \sqrt{\frac{2 h}{g}} = t $$
Un esempio pratico
Un punto cade da un'altezza di 20 metri (h=20).
Tocca il suolo dopo 2,02 secondi
$$ t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2\cdot 20}{9.8}} = 2,02 sec.$$
La caduta con velocità iniziale
Se il corpo fosse gettato verso il basso, avrebbe anche una velocità iniziale (v0) non nulla da considerare.
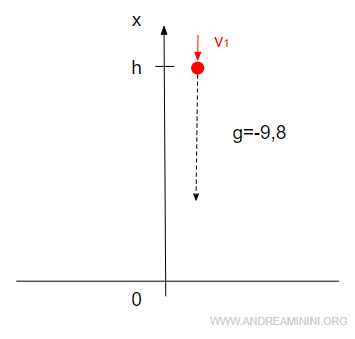
In questo caso la velocità di caduta dipende anche dalla velocità iniziale.
$$ v = v_0 + \sqrt{ 2g (h-x) } $$
Con qualche passaggio algebrico il tempo di caduta diventa
$$ t(x) = \frac{-v_0+\sqrt{v_0^2+2g(h-x)}}{g} $$
Il moto di un corpo lanciato verso l'alto
Lo studio del moto verticale in senso opposto è simile.
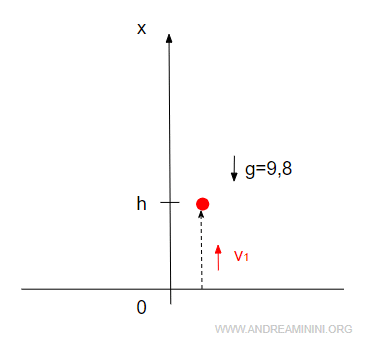
Se lanciassi un sasso dal basso verso l'alto dovrei partire sempre dalla formula
$$ v(t) = v_0 + \int_{t_0}^{t} a(t) \: dt = v_0 + a(t-t_0) $$
Dove v0 è la velocità iniziale del sasso conseguente alla forza con cui lo lancio.
L'accelerazione dipende sempre dalla forza di gravità g ma questa volta si oppone alla velocità del corpo.
$$ v(t) = v_0 + (-g)(t-t_0) $$
$$ v(t) = v_0 - g(t-t_0) $$
Quindi, la formula della velocità di salità è
$$ v(t) = v_0 - g(t-t_0) $$ se t0=0 posso scrivere anche $$ v(t) = v_0 - gt $$
Adesso posso calcolare la legge oraria a partire dalla formula generale del moto uniformemente accelerato
$$ x(t) = \frac{1}{2} a(t-t_0)^2+v_0(t-t_0)+x_0 $$
sostituisco a=-g
$$ x(t) = \frac{1}{2} (-g)(t-t_0)^2+v_0(t-t_0)+x_0 $$
considero l'istante iniziale t0=0
$$ x(t) = \frac{1}{2} (-g)(t)^2+v_0(t)+x_0 $$
e la posizione iniziale x0=0
$$ x(t) = \frac{1}{2} (-g)(t)^2+v_0(t) $$
$$ x(t) = v_0 t - \frac{1}{2} gt^2 $$
In questo caso il moto verso l'alto rallenta progressivamente fino a fermarsi a causa dell'accelerazione negativa (-g).
Quando si arresta la salita?
Per saperlo basta mettere a zero la formula della velocità di salita
$$ v(t) = v_0 - gt = 0 $$
$$ v_0 - gt = 0 $$
$$ v_0 = gt $$
La velocità di salita si arresta nel seguente istante
$$ t = \frac{v_0}{g} $$
A quale altezza si arresta la salita?
Una volta conosciuto l'istante in cui si azzera la velocità di salita, basta sostituirlo alla legge oraria.
$$ x(t) = v_0 t - \frac{1}{2} gt^2 $$
$$ x(t) = v_0 (\frac{v_0}{g}) - \frac{1}{2} g(\frac{v_0}{g})^2 $$
$$ x(t) = \frac{v_0^2}{g} - \frac{1}{2} g (\frac{v_0^2}{g^2}) $$
$$ x(t) = \frac{2v_0^2-v_0^2}{2g} $$
$$ x(t) = \frac{v_0^2}{2g} $$
Nota. Si tratta dell'altezza massima raggiunta dal corpo con il moto verticale in salita. Da questo punto comincia la caduta verso il basso.
Dopo quanto tempo dal lancio il corpo cade a terra?
Per saperlo devo sommare il tempo di salita e di caduta del corpo.
$$ t= \frac{v_0}{g} + \sqrt{ \frac{2h}{g} } $$
Sostituisco h con il punto di massima altezza raggiunto dal corpo
$$ t= \frac{v_0}{g} + \sqrt{ \frac{2\frac{v_0^2}{2g}}{g} } $$
$$ t= \frac{v_0}{g} + \sqrt{ \frac{v_0^2}{g^2} } $$
$$ t= \frac{v_0}{g} + \frac{v_0}{g} $$
$$ t= 2 \frac{v_0}{g} $$
In questo caso il lancio avviene da terra (h=0) quindi il tempo di caduta è uguale al tempo di salita.
Quindi il tempo complessivo è due volte il tempo di salita.
E così via.
