Resistori in serie
Due resistori R1 e R2 possono essere semplificati in un solo resistore equivalente Req $$ v = iR_1+iR_2 = i(R_1+R_2)=iR_{eq} $$ dove $$ R_{eq}=R_1+R_2 $$
I due resistori R1 e R2 sono percorsi dalla stessa corrente (i).
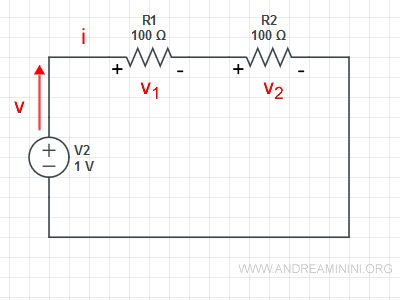
Secondo la legge di Ohm la tensione dei resistori è
$$ v_1 = iR_1 $$
$$ v_2 = iR_2 $$
In base alla legge di Kirchhoff delle tensioni (KVL) la somma delle tensioni si annulla.
$$ -v+v_1+v_2=0 $$
Nota. In questo caso sto percorrendo il circuito in senso orario. Se lo percorressi in senso antiorario il risultato sarebbe stato identico anche se con segni opposti: $$ v-v_1-v_2=0 $$
Quindi
$$ v = v_1+v_2 $$
$$ v = iR_1+iR_2 $$
$$ v = i(R_1+R_2) $$
La tensione ai terminali del circuito è sempre la stessa.
Nota. Se i resistori in serie fossero più di due posso sommarli tutti insieme $$ R_1+R_2+...+R_n $$
La regola del partitore di tensione
La tensione del generatore di un circuito si ripartisce nei resistori in modo direttamente proporzionale alle loro resistenze.
Pertanto, più alta è la resistenza del resistore, maggiore sarà la caduta di tensione.
Il principio della divisione della tensione
La regola del partitore di tensione mi permette di calcolare il voltaggio in uscita da ogni resistori in serie $$ v_1 = \frac{R_1}{R_1+R_2} v $$ $$ v_2 = \frac{R_2}{R_1+R_2} v $$
Ovviamente, se i resistori fossero più di uno per trovare la tensione del generatore dopo l'ennesimo resistore (Rn) dovrei scrivere.
$$ v_n = \frac{R_n}{R_1+...+R_n} v $$
Esempio
In questo circuito ci sono due resistori in serie
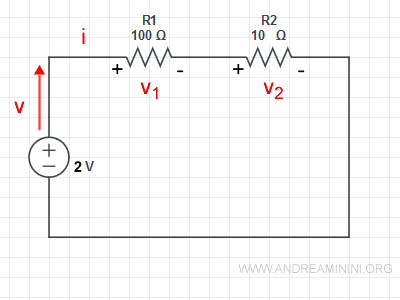
Le tensioni in uscita dal resistore R1 e R2 sono
$$ v_1 = \frac{R_1}{R_1+R_2} v = \frac{100}{100+10} 2 = \frac{100}{55} = 1.8 v $$
$$ v_2 = \frac{R_2}{R_1+R_2} v = \frac{10}{100+10} 2 = \frac{10}{55} = 0.18 v $$
E così via.
