Diagramma di Bode

Il diagramma di Bode è un metodo di rappresentazione della risposta armonica in funzione della pulsazione (w), associata a una funzione di trasferimento di un sistema.

La rappresentazione si basa sulle coordinate polari della W(jw).

Il diagramma di Bode è composto da due diagrammi perché la funzione di risposta armonica è a valori complessi.

• Diagramma del modulo. Il primo diagramma rappresenta il modulo |W(jw)| al variare della pulsazione w. Il modulo è espresso sulle ordinate in decibel. E' anche detto diagramma delle ampiezze o diagramma alfa (α). Rappresenta la parte reale del numero complesso.
  
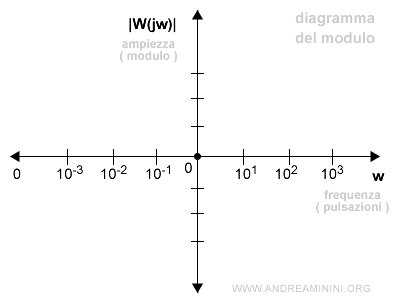
• Diagramma della fase. Il secondo diagramma rappresenta la fase di W(jW) al variare della pulsazione w. La fase è espressa sulle ordinate in gradi o radianti. E' anche detto diagramma degli argomenti o diagramma beta (β).Rappresenta la parte immaginaria del numero complesso.
  

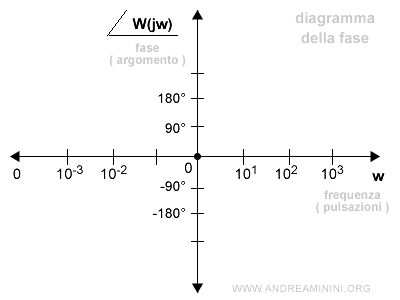
In entrambi i diagrammi l'ascisse non misura semplicemente la pulsazione w bensì il logaritmo di w. In genere, si tratta del logaritmo naturale o decimale.

Quindi le frequenze sull'asse delle ascisse non sono in scala lineare e non sono equidistanziate.

Si dice decade è un rapporto tra due frequenze w₂/w₁ pari a 10.

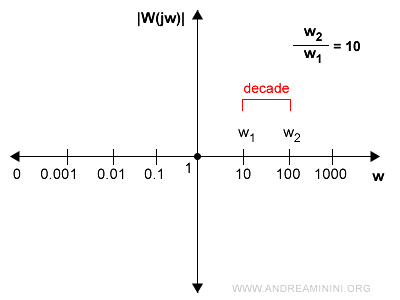
L'intersezione degli assi corrisponde al valore 1. Lo zero, invece, non è rappresentato perché corrisponde al limite di sinistra.

Nelle ordinate si indica il logaritmo o il valore lineare di |W(jw)| nel primo diagramma e la fase di W(jw) nel secondo.

I diagrammi di Bode sono anche detti diagrammi logaritmici di risposta armonica.

Perché si usa la scala logaritmica? Essendo un'analisi nel dominio della frequenza, la scala logaritmica permette di rappresentare in forma compatta una più ampia escursione della frequenza e della pulsazione perché contrae i valori più elevati ed espande quelli più bassi.

I diagrammi possono essere

• in scala logaritmica se sia l'ascisse e sia le ordinate sono in scala logaritmica.
  
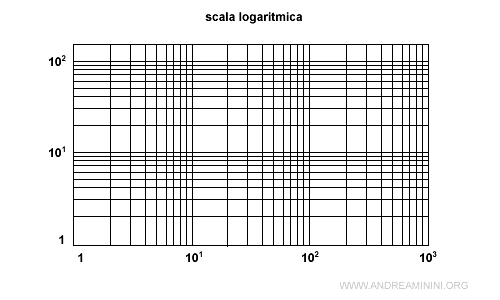
• in scala semi-logaritmica se soltanto l'ascisse è in scala logaritmica
  

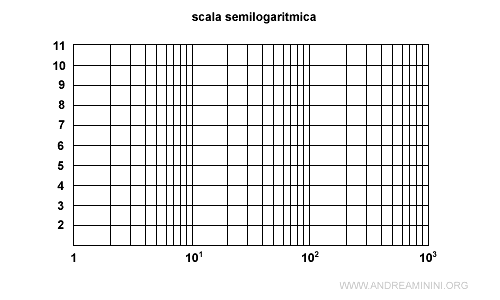
A volte la scala delle ampiezze è gratuata in decibel.

$$ B = 20 \log_{10} A $$

Esempio. Il modulo |W(js)|db espresso in decibel è $$ |W(jw)|_{db} = 20 \log |W(jw)| $$ Ecco un esempio della scala del modulo sulle ordinate in decibel.

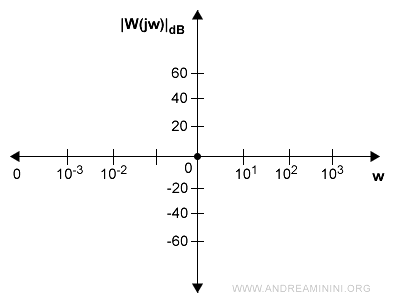
dove 20dB equivale a un guadagno di 10, 40dB a un guadagno di 100, e così via. L'origine 0 indica nessun guadagno nel segnale (guadagno zero). Mentre -20dB corrisponde a un'attenuazione di dieci volte (0,1), -40dB a un'attenuazione di cento volte (0,01). La completa cancellazione del segnale corrisponde a -∞. Va detto che il precedente diagramma è comunque in scala semilogaritmica perché sulle ordinate le grandezze sono rappresentate in scala lineare anche se il decibel le trasforma in scala logaritmica.

Quindi, il diagramma del modulo si presenta in questa forma

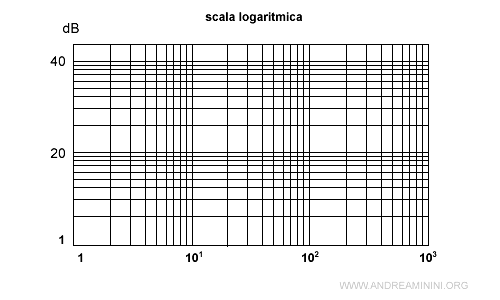
Nota. Il decibel è un'unità logaritmica che si usa per misurare il guadagno di amplificazione (rapporto tra l'ampiezza del segnale di uscita e quella del segnale in ingresso). Il decibel non è un'unità di misura. E' una grandezza adimensionale, serve a rappresentare in scala logaritmica una certa grandezza che ha una sua unità di misura. Per questo motivo, se uso i decibel devo specificare nel diagramma anche l'unità di misura a cui sono applicati. In genere, in ingegneria e fisica i decibel sono riferiti a potenze. Pertanto, se non è indicato diversamente, devo considerare 20 log₁₀ per la proprietà dei logaritmi. $$ 10 \log_{10} ( \frac{a}{b})^2 = 20 \log_{10} ( \frac{a}{b}) $$

I vantaggi della scala logaritmica

La scala logaritmica nel diagramma di Bode ha diversi vantaggi

• Rappresenta grandezze estese in forma sintetica, perché amplia le grandezze più piccole e comprime quelle più grandi
• La somma dei diagrammi dei singoli sistemi a cascata determina il diagramma del sistema complessivo.

  Nota. La risposta armonica del sistema complessivo è pari al prodotto delle risposte armoniche dei singoli sistemi che lo compongono. Mentre la fase del sistema complessivo è pari alla somma delle fasi.

• Il diagramma della risposta armonica di un sistema in forma fattorizzata può essere scomposto in una somma di diagrammi elementari. Ogni diagramma elementare è associato un fattore della funzione iniziale.

La funzione di trasferimento di Bode

Posso rappresentare la funzione di trasferimento G(s) di un sistema

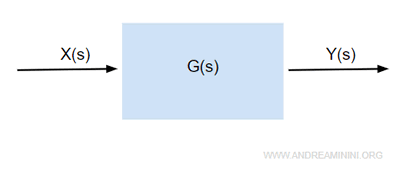
nella rappresentazione di Bode

$$ G(s) = K \cdot \frac{ \ (1+τ_1s) \cdot (1+τ_2s) \cdot \cdot \cdot ( 1 \cdot \frac{2sδ_1}{ω_{n,1}} + \frac{s^2}{ω_{n,1}^2} ) \cdot ( 1 \cdot \frac{2sδ_2}{ω_{n,2}} + \frac{s^2}{ω_{n,2}^2} ) \cdots }{ s^h \cdot (1+τ'_1s) \cdot (1+τ'_2s) \cdot \cdot \cdot ( 1 + \frac{2sδ'_1}{ω_{n,1}^{'}} + \frac{s^2}{ω_{n,1}^{'2}} ) \cdot ( 1 + \frac{2sδ'_2}{ω_{n,2}^{'}} + \frac{s^2}{ω_{n,2}^{'2}} ) \cdots } $$

dove K è il guadagno di Bode

$$ K = K' \cdot \frac{ τ'_1 \cdot τ'_2 \cdots ω_{n,1}^{2} \cdot ω_{n,2}^{2} \cdots }{ τ_1 \cdot τ_2 \cdots ω_{n,1}^{'2} \cdot ω_{n,2}^{'2} \cdots } $$

Gli altri parametri sono

• ω_n è la pulsazione naturale
• δ è il coefficiente di smorzamento
• τ è la costante di tempo

Come si costruisce? Il processo per ottenere la funzione di trasferimento di Bode è un po' lungo e complesso. Per questa ragione evito di spiegarlo qui. Per approfondimenti rimando agli appunti su come costruire la funzione di trasferimento di Bode.

Sostituisco la s=jω

$$ G(s) = K \cdot \frac{ \ (1+τ_1jω) \cdot (1+τ_2jω) \cdot \cdot \cdot ( 1 + \frac{2jωδ_1}{ω_{n,1}} + \frac{(jω)^2}{ω_{n,1}^2} ) \cdot ( 1 + \frac{2jωδ_2}{ω_{n,2}} + \frac{(jω)^2}{ω_{n,2}^2} ) \cdots }{ (jω)^h \cdot (1+τ'_1jω) \cdot (1+τ'_2jω) \cdot \cdot \cdot ( 1 + \frac{2jωδ'_1}{ω_{n,1}^{'}} + \frac{(jω)^2}{ω_{n,1}^{'2}} ) \cdot ( 1 + \frac{2jωδ'_2}{ω_{n,2}^{'}} + \frac{(jω)^2}{ω_{n,2}^{'2}} ) \cdots } $$

$$ G(s) = K \cdot \frac{ \prod_{i} (1+τ_ijω) }{ (jω)^h \cdot \prod_{i} (1+τ'_ijω) } \cdot \frac{ \prod_{i} ( 1 + \frac{2jωδ_i}{ω_{n,i}} + \frac{(jω)^2}{ω_{n,i}^2} ) }{ \prod_{i} ( 1 + \frac{2jωδ'_i}{ω_{n,i}^{'}} + \frac{(jω)^2}{ω_{n,i}^{'2}} ) } $$

Per la proprietà dei numeri complessi il quadrato dell'unità immaginaria è j²=-1.

$$ G(s) = K \cdot \frac{ \prod_{i} (1+τ_ijω) }{ (jω)^h \cdot \prod_{i} (1+τ'_ijω) } \cdot \frac{ \prod_{i} ( 1 + \frac{2jωδ_i}{ω_{n,i}} + (j^2) \cdot \frac{(ω)^2}{ω_{n,i}^2} ) }{ \prod_{i} ( 1 + \frac{2jωδ'_i}{ω_{n,i}^{'}} + (j^2) \cdot \frac{(ω)^2}{ω_{n,i}^{'2}} ) } $$

$$ G(s) = K \cdot \frac{ \prod_{i} (1+τ_ijω) }{ (jω)^h \cdot \prod_{i} (1+τ'_ijω) } \cdot \frac{ \prod_{i} ( 1 + \frac{2jωδ_i}{ω_{n,i}} + (-1) \cdot \frac{ω^2}{ω_{n,i}^2} ) }{ \prod_{i} ( 1 + \frac{2jωδ'_i}{ω_{n,i}^{'}} + (-1) \cdot \frac{ω^2}{ω_{n,i}^{'2}} ) } $$

$$ G(s) = \frac{K}{ (jω)^h } \cdot \frac{ \prod_{i} (1+τ_ijω) }{ \prod_{i} (1+τ'_ijω) } \cdot \frac{ \prod_{i} ( 1 + \frac{2jωδ_i}{ω_{n,i}} - \frac{ω^2}{ω_{n,i}^2} ) }{ \prod_{i} ( 1 + \frac{2jωδ'_i}{ω_{n,i}^{'}} - \frac{ω^2}{ω_{n,i}^{'2}} ) } $$

Dove K è la costante di guadagno.

• con h=0 è la costante di guadagno statico della risposta armonica (ω=0)
• con h=1 è la costante di velocità
• con h=2 è la costante di accelerazione.

Nota. Per analizzare il comportamento della funzione è importante soprattutto analizzare i poli al denominatore della funzione, perché hanno un significato fisico e influenzano l'evoluzione dinamica del sistema.

Quest'ultima forma fattorizzata ha diversi vantaggi:

1. Esprime il modulo in decibel
2. Mi permette di costruire il diagramma del modulo e della fase tramite il principio di sovrapposizione

Cos'è il principio di sovrapposizione?

Consiste nello scomporre e esaminare i singoli fattori della funzione di trasferimento G(s) in forma fattorizzata. Poi, sommare i moduli in decibel e le fasi in gradi (o radianti) di ciascun fattore (componente elementare). Il risultato finale è il diagramma di Bode della funzione di trasferimento.

Le componenti della funzione di trasferimento nella forma di Bode sono:

$$ K $$	guadagno
$$ (jω)^h $$	monomio
$$ (1+τ_ijω) $$	binomio al numeratore
$$ \frac{1}{(1+τ_ijω)} $$	binomio al denominatore
$$ ( 1 + \frac{2jωδ'_i}{ω_{n}^{'}} - \frac{ω^2}{ω_{n}^{'2}} ) $$	trinomio al numeratore
$$ \frac{1}{( 1 + \frac{2jωδ'_i}{ω_{n}^{'}} - \frac{ω^2}{ω_{n}^{'2}} ) } $$	trinomio al denominatore

A questo punto devo analizzare singolarmente le componenti elementari.

Il diagramma del modulo

Nel diagramma del modulo la funzione di trasferimento è espressa in decibel.

$$ | G(jw) |_{db} = 20 \log | G(jw) | $$

Dove jw è un numero complesso.

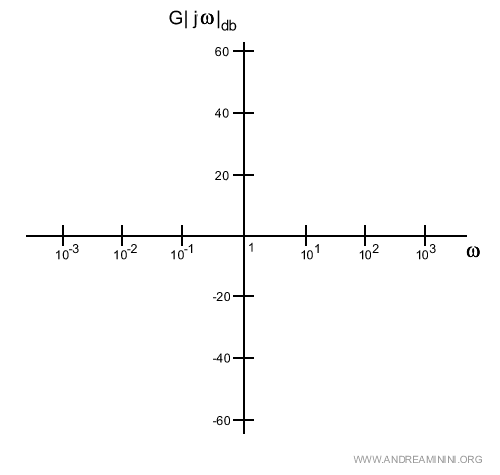
Per semplicità in questo caso utilizzo il logaritmo in base 10.

Con opportune modifiche si potrebbe usare anche il logaritmo naturale (neperiano).

Nota. Sapendo che, secondo le proprietà dei logaritmi, il rapporto di logaritmi è uguale alla differenza di logaritmi $$ \log_b( \frac{a}{c} ) = \log_b a - log_b c $$ il logaritmo di un prodotto è uguale alla somma dei logaritmi $$ \log_b(a \cdot c) = \log_b a + log_b c $$ e il logaritmo di una potenza è uguale alla potenza per il logaritmo $$ \log_b a^n = n \cdot \log_b a $$.

Posso riscrivere il modulo della funzione di trasferimento in questa forma.

$$ | G(jw) |_{db} = 20 \log |K| - 20 \cdot h \cdot \log |jw| + \\ + \sum_i 20 \log | 1+τ_ijω | + \sum_i 20 \log | 1 + \frac{2jωδ_i}{ω_{n}} - \frac{ω^2}{ω_{n}^{2}} | - \\ - \sum_i 20 \log |1+τ'_ijω| - \sum_i 20 \log | 1 + \frac{2jωδ'_i}{ω_{n,i}^{'}} - \frac{ω^2}{ω_{n,i}^{'2}} | $$

Ora costruisco il diagramma del modulo delle singole componenti.

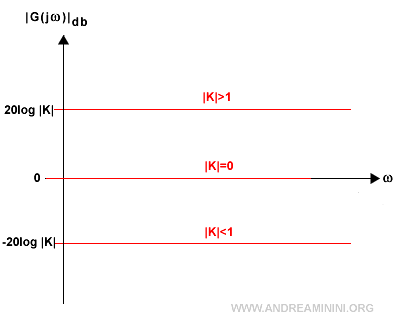
• Guadagno K
  $$ | G(jw)|_{db}^A = 20 \log |K| $$ Il modulo del guadagno è uguale a una costante positiva 20 log |K| se |K|>1, è uguale a zero se |K|=1, uguale a una costante negativa -20 log |K| se |K|<1.
  

  
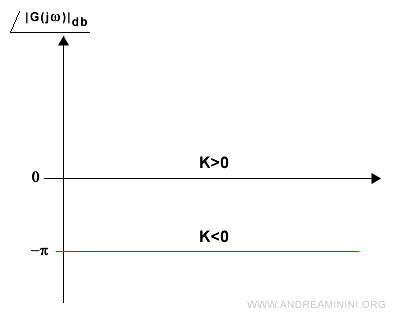
  La fase è uguale a 0 se K è un numero positivo (K>0) oppure a -π se K è negativo (K<0).
  

• Il monomio (jω)
  $$ | G(jw)|_{db}^B = -20 \cdot h \log |jω| $$ Il modulo del monomio è una perdita pari a 20*h decibel per decade. Dove h è il numero dei poli nell'origine.
  
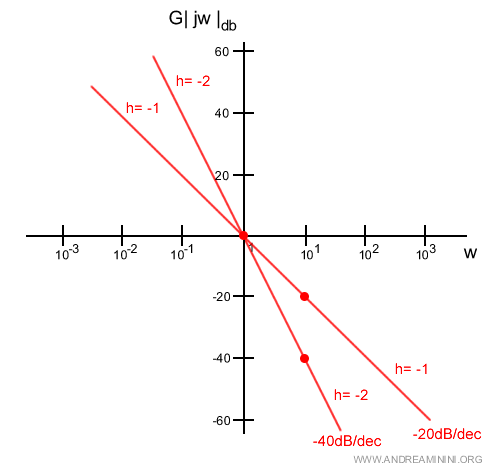
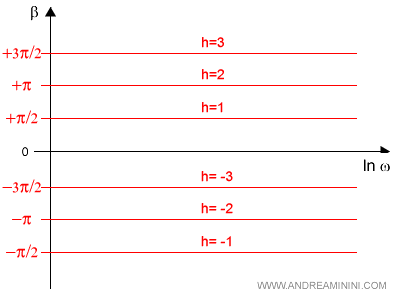
  La fase del monomio è una retta costante pari a +90° per gli zeri (h=1) e -90° per i poli (h=-1) moltiplicati per la molteplicità (h). Dove h>0 è la molteplicità degli zeri e h<0 è la molteplicità dei poli.
  
• Il binomio (1+jτω)
  Il modulo del binomio al numeratore si calcola con l'analisi asintotica. $$ | G(1+jτω)|_{db}^C = 20 \log |1+jτω| $$ E' nullo fino 1/τ e ha un guadagno di 20 decibel per decade dopo 1/τ.
  
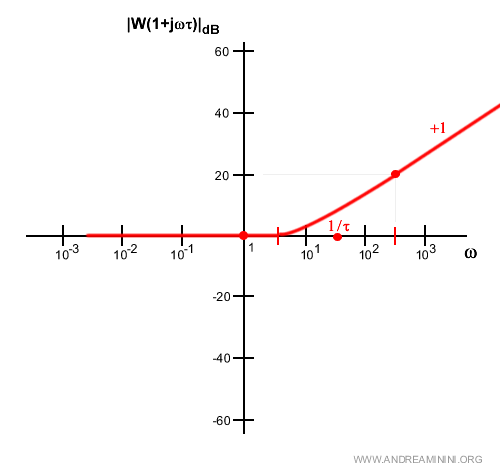
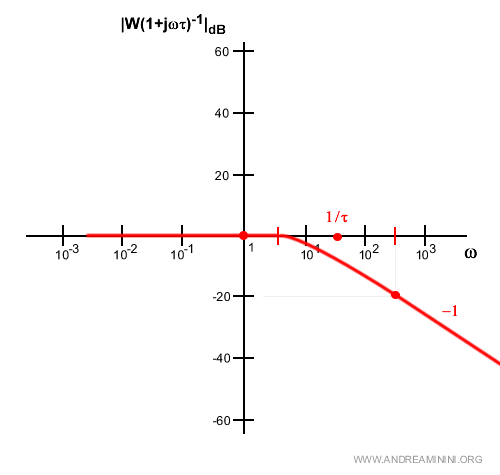
  Il modulo del binomio al denominatore ha andamento opposto. $$ | G(jω)|_{db}^C = 20 \log \frac{1}{|1+jτω|} $$ $$ | G(jω)|_{db}^C = - 20 \log |1+jτω| $$ E' nullo fino 1/τ e ha una perdita di 20 decibel per decade dopo 1/τ.
  
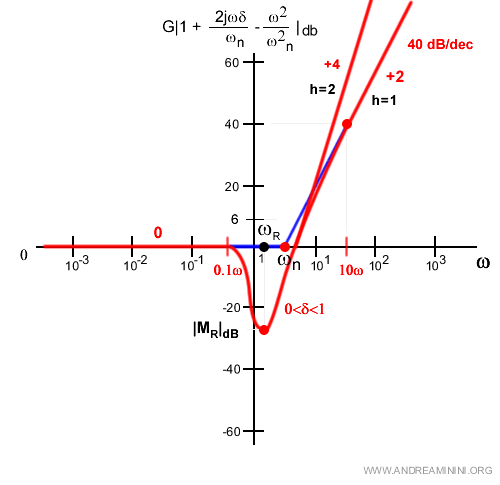
• Il trinomio
  Il modulo del trinomio al numeratore si calcola con l'analisi asintotica. $$ | G( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_n^2} )|_{db}^D = 20 \log |( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_n^2} )| $$ E' generalmente nullo fino a una decade prima della pulsazione naturale ω_n poi ha un guadagno di 40 decibel per decade dopo ω_n. L'andamento nell'intorno di ω_n è però fortemente influenzato dal coefficiente di smorzamento δ.
  
  Il modulo del trinomio al denominatore ha andamento opposto. $$ | G( ( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_n^2} )^{-1} )|_{db}^D = 20 \log \frac{1}{|( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_n^2} )|} $$ $$ | G(jω)|_{db}^D = - 20 \log |1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_n^2}| $$ Anche in questo caso è generalmente nullo fino a una decade prima della pulsazione naturale ω_n, poi ha una perdita di 40 decibel per decade dopo ω_n. Nell'intorno di ω_n il comportamento della funzione è fortemente influenzato dal coefficiente di smorzamento δ.
  

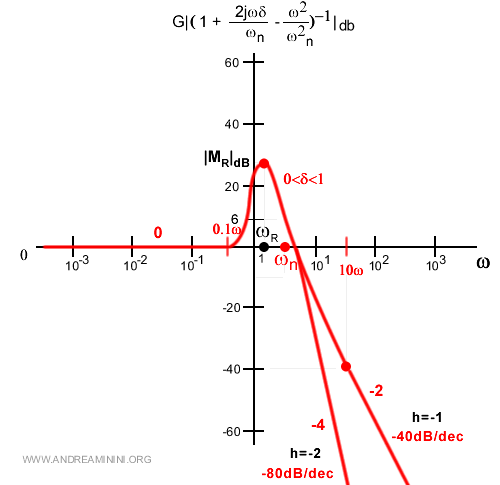
  Nota. La molteplicità h aumenta la pendenza del grafico. Se h=-2 la pendenza diventa -80 dB ogni decade.

La sovrapposizione grafica

Dopo aver tracciato i grafici delle singole componenti della funzione, devo soltanto sorvrapporli in un diagramma e sommare le pendenze in modo algebrico.

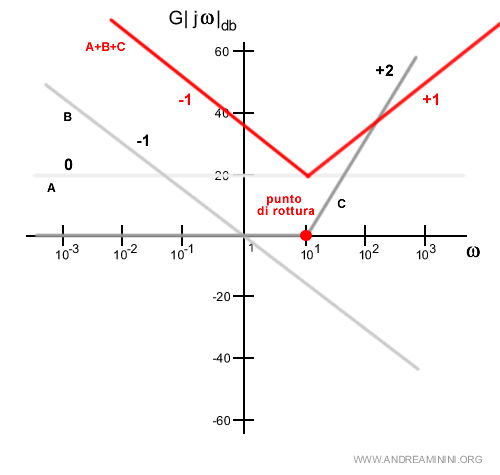
Nei punti di rottura la pendenza aumenta, diminuisce o resta costante.

Il diagramma della fase

Anche in questo caso bisogna guardare le singole componenti:

• Costante K
  L'analisi della costante per costruire la fase è molto semplice
  
  
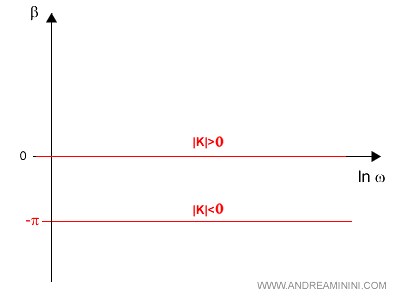
• Monomio
  Il fattore monomio causa uno sfasamento/ritardo di -90° su tutte le frequenze a seconda della molteplicità h. Se h>0 sono zeri, se h<0 sono poli.
  
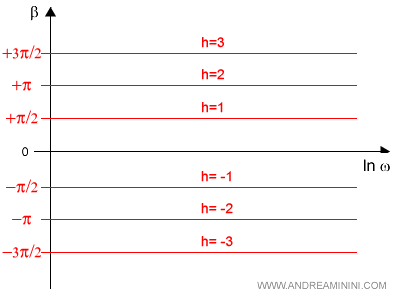
• Binomio
  Nel caso del trinomio la fase tende a ±90° a seconda del segno della variabile τ, della molteplicità h e se si tratta di zeri (binomio al numeratore)
  
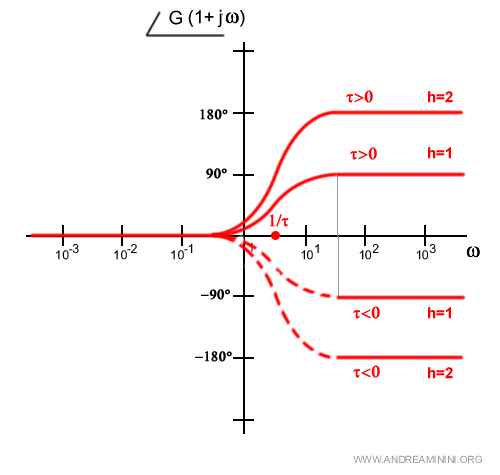
  oppure di poli (binomio al denominatore)
  
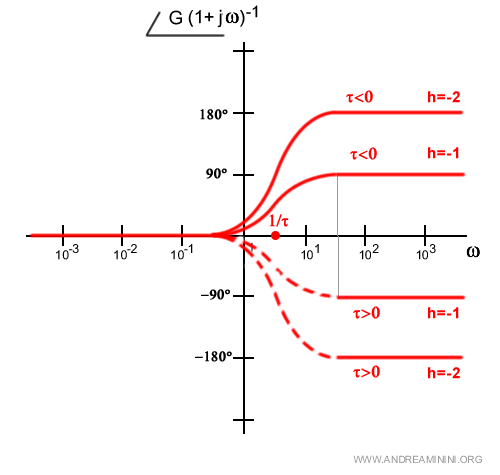
• Trinomio
  Nel caso del trinomio la fase tende a ±180° a seconda del segno del coefficiente di smorzamento δ e se si tratta di zeri ( trinomio al numeratore )
  
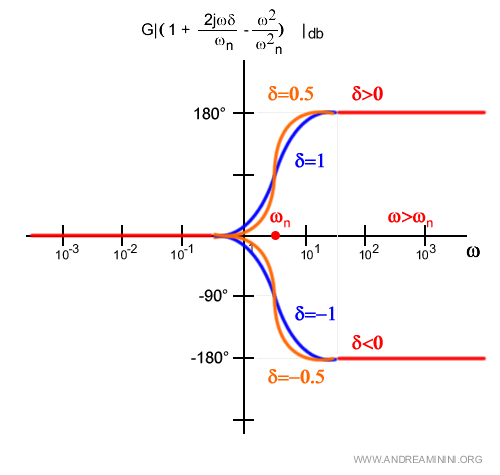
  oppure di poli ( trinomio al denominatore ).
  

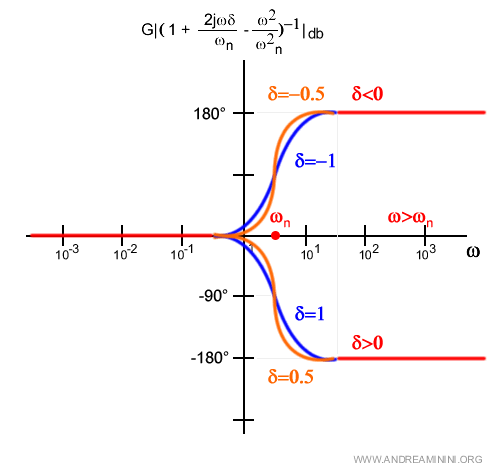
E così via.