Il fattore monomio nel diagramma di Bode

Il modulo

Il modulo del fattore monomio |G(jw)| espresso in decibel è

$$ |G(jw)|db = 20 \log jw $$

poiché j è l'unità complessa ( modulo unitario ) posso scrivere semplicemente

$$ |G(jw)|db = 20 \log w $$

Dove w è la pulsazione.

Si tratta di un termine lineare rispetto a log w, una retta passante per l'origine con pendenza 20 db per decade.

Nota. In questi appunti per log(x) intendo il logaritmo è su base 10 ossia log₁₀.

Per costruire la retta nel diagramma del modulo mi basta calcolare due punti.

Ad esempio, prendendo la pulsazione w=1 ottengo

$$ 20 \log 1 = 0 $$

Nota. Il logaritmo di 1 è sempre pari a zero perché qualsiasi numero elevato a zero dà come risultato uno. Per un approfondimento rimando agli appunti sui logaritmi.

Questo dimostra che la retta passa sempre per l'origine ossia 10⁰=1.

Se il fattore jw si trova al numeratore è uno zero nell'origine.

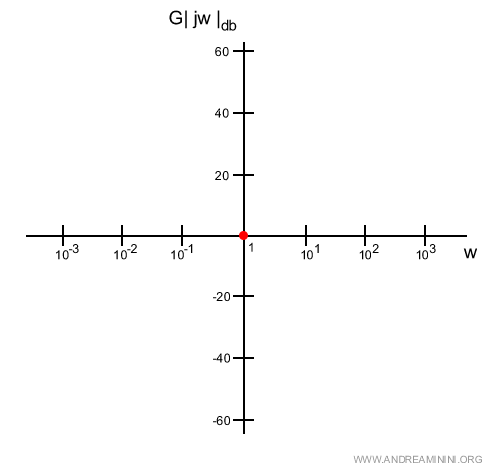
Poi prendo in considerazione w=10.

Il logaritmo di 10 è uguale a 1, quindi 20 log 10 = 20.

$$ 20 \log 10 = 20 \cdot 1 = 20 $$

Con questi due punti posso tracciare la retta sul diagramma del modulo.

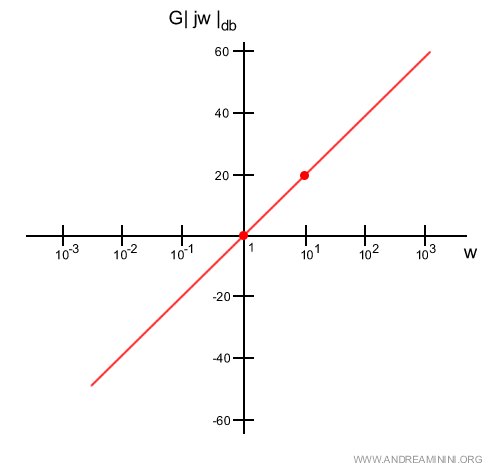
L'inclinazione della retta dipende dal numero degli zeri.

Nota. Ovviamente, se h=0 la retta non si può tracciare perché vuol dire che non esistono zeri nell'origine.

In questo caso l'inclinazione è pari a 20 db perché c'è un guadagno di amplificazione di 20 decibel per decade.

Nel caso in cui ci fossero più zeri ( es. h zeri )

$$ |G(jw)|db = 20 \log w^h $$

Per la proprietà dei logaritmi la potenza è uguale al prodotto di logaritmi.

$$ |G(jw)|db = 20 \cdot h \log w $$

Pertanto, l'inclinazione della retta sarebbe più marcata.

Ad esempio, con h=2 zeri nell'origine ci sarebbe un guadagno di 40 decibel per decade.

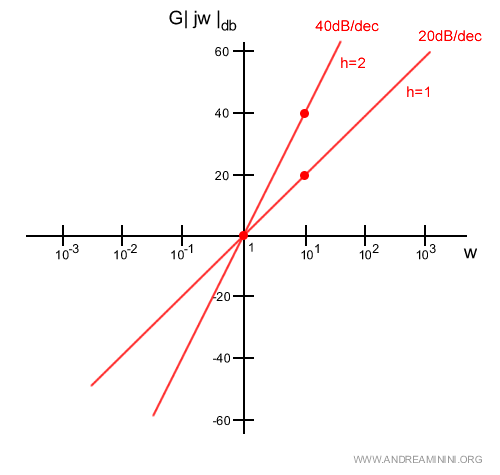
Poiché il guadagno è sempre multiplo di 20 dB, spesso le rette 20db/dec e 40 db/dec sono indicate semplicemente con +1 e +2.

E' una convenzione più compatta.

Nota. Se il monomio jw si trova al denominatore c'è invece un polo nell'origine. Il procedimento di calcolo del modulo è molto simile al caso precedente. $$ |W(jw)^{-1}|_{db} = 20 \log | \frac{1}{jw} | $$ il rapporto del logaritmo è uguale alla differenza $$ |W(jw)^{-1}|_{db} = 20 \log |1| - 20 \log |jw| $$ $$ |W(jw)^{-1}|_{db} = 0 - 20 \log |jw| $$ Essendo j un modulo unitario posso scrivere $$ |W(jw)^{-1}|_{db} = - 20 \log |w| $$ In questo caso l'inclinazione è negativa con una pendenza pari a -20 db perché perde 20 decibel per ogni decade.

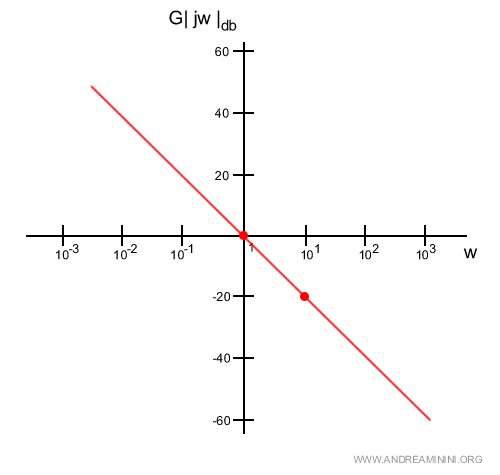
Nel caso in cui ci fossero più poli ( es. h poli ) $$ |W(jw)^{-1}|_{db} = 20 \log | \frac{1}{(jw)^h} | $$ il rapporto del logaritmo è uguale alla differenza $$ |W(jw)^{-1}|_{db} = 20 \log |1| - 20 \cdot h \log |jw| $$ $$ |W(jw)^{-1}|_{db} = 0 - 20 \cdot h \log |jw| $$ Essendo j un modulo unitario posso riscriverla nella forma $$ |W(jw)^{-1}|_{db} = - 20 \cdot h \log |w| $$ Con h=2 poli nell'origine ci sarebbe una perdita di -20dB per decade.

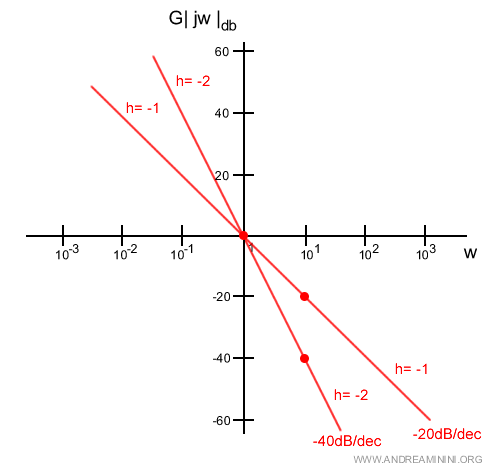
Le due rette -20dB/dec e -40dB/dec sono anche indicate in forma più compatta come -1 e -2.

La fase

1] Poli nell'origine

Il fattore monomio causa uno sfasamento/ritardo di -90° su tutte le frequenze per i poli nell'origine.

Si tratta di una retta orizzontale con intercetta sulle ordinate pari a -π/2.

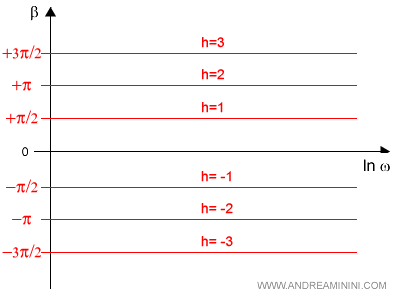
E' una costante pari a

$$ -h \cdot \frac{π}{2} $$

Dove h è la molteplicità dei poli.

2] Zeri nell'origine

Il fattore monomio causa un anticipo di -90° su tutte le frequenze per i zeri nell'origine.

Si tratta di una retta orizzontale con intercetta sulle ordinate pari a π/2.

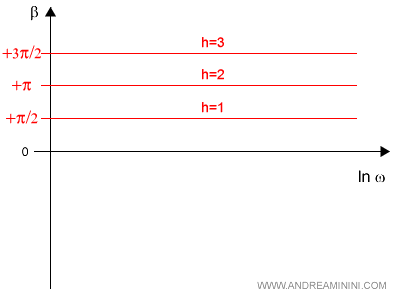
La molteplicità (h) degli zeri nel monomio modifica l'intercetta della retta sull'asse delle ordinate.

$$ +h \cdot \frac{π}{2} $$

E così via.