Il binomio sul diagramma di Bode
Il modulo
Il modulo del fattore binomio |G(1+τjω)| espresso in decibel è
$$ |G(1+τjω)|_{dB} = 20 \log |1+τjω| $$
Poiché j è l'unità complessa posso sostituirla con 1 e ometterla
$$ |G(1+τjω)|_{dB} = 20 \log |1+τω| $$
Sostituisco il modulo con la radice quadrata delle potenze.
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1^2+(τω)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(τω)^2} $$
Per analizzare il binomio ricorro all'analisi asintotica.
Cos'è l'analisi asintotica? E' un'analisi approssimata che si effettua spezzando la funzione in due o più parti e analizzando il comportamento della funzione per ω tendente a zero e per ω tendente a infinito, quando i suoi termini sono molto piccoli o molto grandi.
In questo caso il binomio è composto da 1+(τω)2.
Essendo 1 e τ delle costanti, concentro l'attenzione sulla pulsazione ω.
Se ω è molto più piccolo di 1/τ
$$ ω << \frac{1}{|τ|} $$
Cosa vuol dire molto più piccolo? Quando si parla di un valore "molto più piccolo" di un altro si intende almeno 10 volte più piccolo, ossia una decade a sinistra sull'asse logaritmico rispetto al valore di riferimento. Nel grafico seguente è il trattino su 0.1ω.
In questo caso posso trascurare il monomio (τω)2 del binomio
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(τω)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1} $$
$$ |G(1+τjω)|_{dB} = 20 \log 1 $$
$$ |G(1+τjω)|_{dB} = 0 $$
Ad esempio, diciamo di aver trovato 1/τ tra 101 e 102
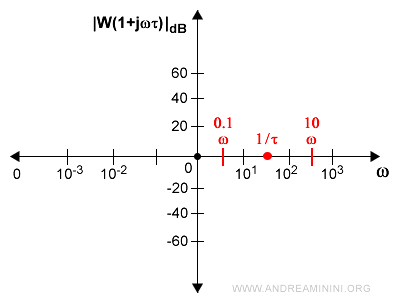
Intorno al punto aggiungo un margine di errore di una decade sia a sinistra (0.1ω) che a destra (10ω).
Questo vuol dire che prima di 0.1 ω l'errore di approssimazione è molto piccolo e la stima è affidabile.
Posso quindi cominciare a tracciare il grafico in modo asintotico per ω tendente a 0.
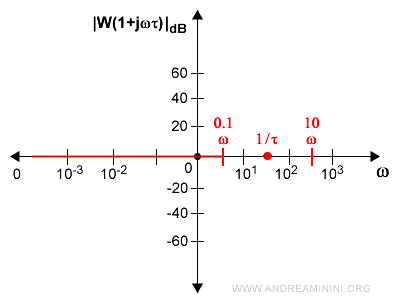
Se ω è molto più grande di 1/τ
$$ ω >> \frac{1}{|τ|} $$
Cosa vuol dire molto più grande? Quando si parla di un valore "molto più grande" di un altro si intende almeno 10 volte più grande rispetto al valore di riferimento, ossia una decade a destra sull'asse logaritmico. Nel grafico è il trattino con 10ω.
In questo caso posso trascurare la costante 1 del binomio
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(τω)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{(τω)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log |τω| $$
Quindi, se ω è molto più grande (almeno dieci volte 10ω) rispetto a 1/τ, la funzione ha un'amplificazione di 20 decibel per decade.
Individuo il punto sul grafico a partire da 10ω, ossia una decade a destra di 1/τ.
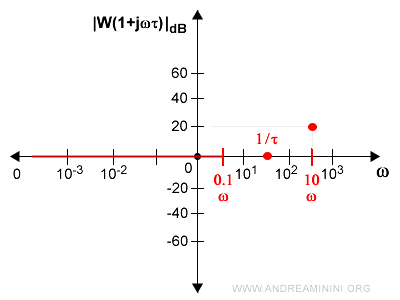
A partire da questo punto il margine d'errore è trascurabile.
Pertanto, posso considerare affidabile l'approssimazione e tracciare il grafico in modo asintotico per ω tendente a ∞.
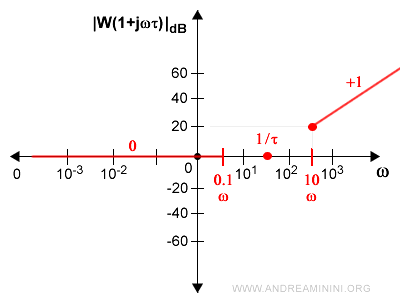
Nota. Su questo tratto del grafico aggiungo "+1" per indicare che ha un guadagno di 20decibel per decade. Sul tratto precedente, a sinistra, aggiungo "0" per indicare che non c'è né un guadagno, né una perdita. Ovviamente, nel caso in cui ci siano delle molteplicità h la pendenza della curva diventa maggiore. $$ |G(1+τjω)|_{dB} = 20 \log |(1+τjω)^h| $$ $$ |G(1+τjω)|_{dB} = 20 \cdot h \cdot \log |1+τjω| $$ Ad esempio se h=2 diventa +2 ossia +40 dB per decade.
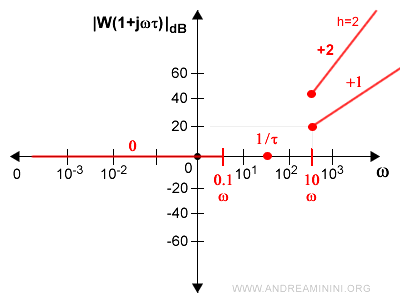
Resta da capire come stimare il valore della funzione nel tratto centrale da 0.1ω a 10ω dove il margine d'errore è più elevato.
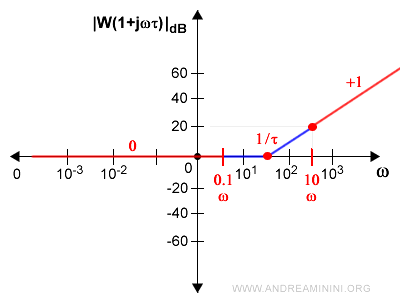
Una soluzione semplice e rapida è tracciare una linea spezzata da 0.1ω a 1/τ e un'altra linea spezzata da 1/τ a 10ω.
 ù
ù
Il punto intermedio 1/τ è anche detto punto di rottura, perché in questo punto varia la pendenza del grafico in modo netto.
Si tratta però di una semplificazione soggetta ad un margine d'errore molto alto nel punto 1/τ.
Per calcolare l'errore in 1/τ sostituisco ω=1/|τ| nella funzione iniziale del binomio.
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(τω)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(τ\frac{1}{|τ|})^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{1+(1)^2} $$
$$ |G(1+τjω)|_{dB} = 20 \log \sqrt{2} $$
Il logaritmo di √2 su base 10 è 0.15
$$ |G(1+τjω)|_{dB} = 20 \cdot 0.15 $$
$$ |G(1+τjω)|_{dB} = 3 $$
Il punto di passaggio della funzione si trova circa 3 decibel sopra 1/|τ|.
E' il punto di massimo errore.
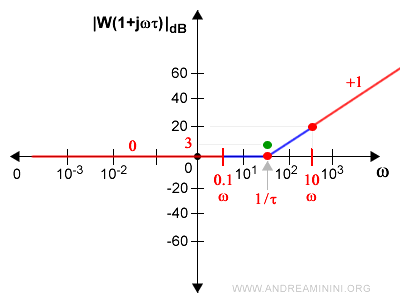
Essendo due tratti continui (0 e 1) è molto probabile che il grafico sia continuo anche nell'intervallo (0.1ω-10ω).
Quindi, per ridurre il margine d'errore intorno al punto di rottura 1/τ posso far passare il grafico per il nuovo punto appena trovato.
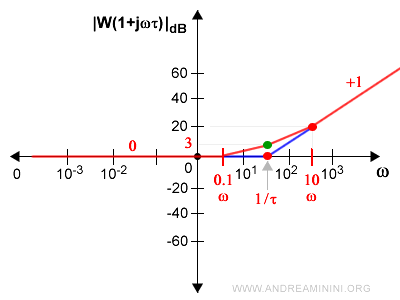
Ora il margine d'errore dell'approssimazione in 1/τ è molto più basso.
Ho così tracciato il modulo del binomio |G(1+τjω)| espresso in decibel sul diagramma di Bode.
Nota. In modo simile posso tracciare anche il binomio al denominatore. $$ |(1+τjω)^{-1}| = \frac{1}{(1+τjω)} $$ ossia $$ |(\frac{1}{(1+τjω)})|_{dB} = 20 \log \sqrt{\frac{1}{1+(τω)^2}} $$ $$ |(\frac{1}{(1+τjω)})|_{dB} = 20 \log \sqrt{\frac{1}{(τω)^2}} $$ $$ |(\frac{1}{(1+τjω)})|_{dB} = - 20 \log \sqrt{1}{(τω)^2} $$ $$ |(\frac{1}{(1+τjω)})|_{dB} = -20 \log |τω| $$ L'andamento grafico è esattamente l'opposto rispetto al precedente.
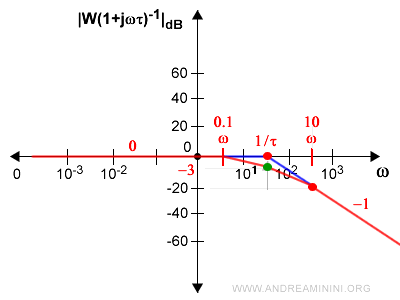
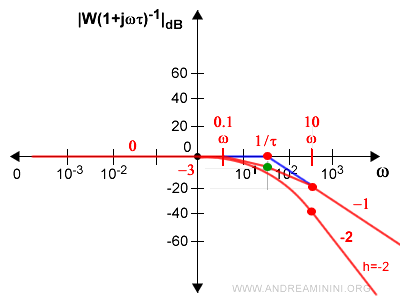
e in caso di molteplicità h di poli la perdita (pendenza negativa) aumenta. $$ |G(\frac{1}{(1+τjω)^h})|_{dB} = -20 \cdot h \cdot \log |τω| $$ Ad esempio, se ci sono due poli al denominatore (h=-2) la pendenza diventa -2 ossia -40dB per decade.
La fase
La fase del binomio si calcola in questo modo
$$ φ(ω)=arg(1+jωτ) = arctg(ωτ) $$
L'arcotangente è il rapporto tra la parte immaginaria (ωτ) e la parte reale (1)
Faccio un calcolo asintotico per frequenze (ω) molto piccole e molto grandi
Se la frequenza ω è molto piccola
La frequenza tende a zero
$$ ω \rightarrow 0 $$
In particolar modo se
$$ ω << \frac{1}{|τ|} $$
prevale la parte reale (1) sulla parte immaginaria (jωτ) perché il valore di ω è molto piccolo
Posso riscrivere la formula in forma asintotica escludendo la parte immaginaria (jωτ).
$$ φ(ω)=arg(1) $$
L'argomento di 1 è uguale a zero.
Quindi, la fase è pari a circa 0° e la stima è abbastanza sicura una decade prima del punto di rottura 1/τ
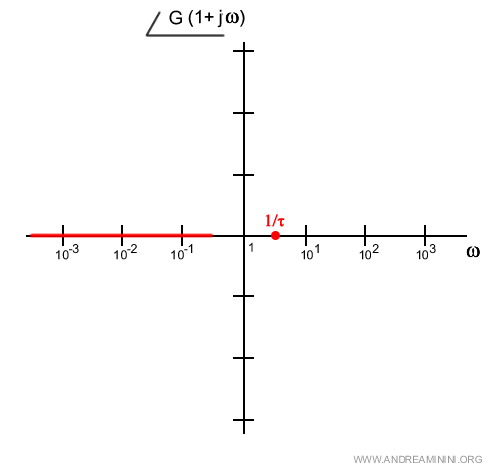
Se la frequenza ω è molto grande
La frequenza tende a infinito
$$ ω \rightarrow ∞ $$
In particolar modo se
$$ ω >> \frac{1}{|τ|} $$
prevale la parte immaginaria (jωτ) sulla parte reale (1) perché il valore di ω è molto grande
Posso riscrivere la formula in forma asintotica escludendo la parte reale (1).
$$ φ(ω)=arg(jωτ) $$
Il risultato dipende dal segno della variabile τ.
- Se τ>0 la fase è circa φ(ω)=90° ( ossia π/2 )
$$ \lim_{ ω \rightarrow ∞ } \arctan(ωτ) = π/2 \:\: con \:\: τ>0 $$
- Se τ<0 la fase è circa φ(ω)=-90° ( ossia -π/2 )
$$ \lim_{ ω \rightarrow ∞ } \arctan(ωτ) = -π/2 \:\: con \:\: τ<0 $$
La stima è abbastanza sicura una decade dopo del punto di rottura 1/τ
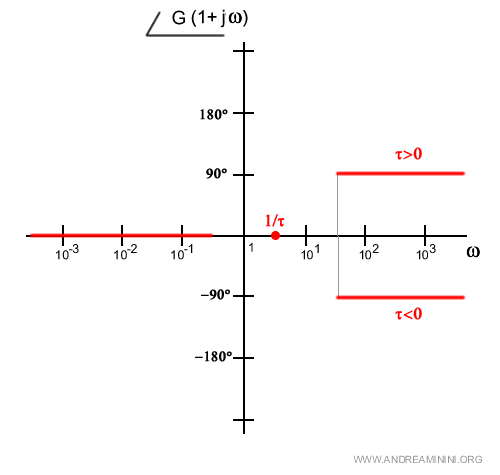
La parte intermedia del grafico è quella più soggetta al margine d'errore.
Uno dei modi più semplici è congiungere gli asintoti o, in alternativa, disegnare un gradino all'altezza del punto di rottura 1/τ.
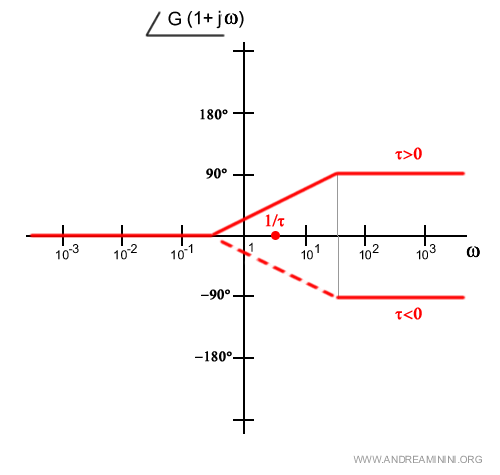
E' comunque sicuro che il segnale passa per +45° in corrispondenza del punto di rottura 1/τ.
Per un disegno più preciso posso usare il grafico dell'arcotangente nel tratto intermedio.
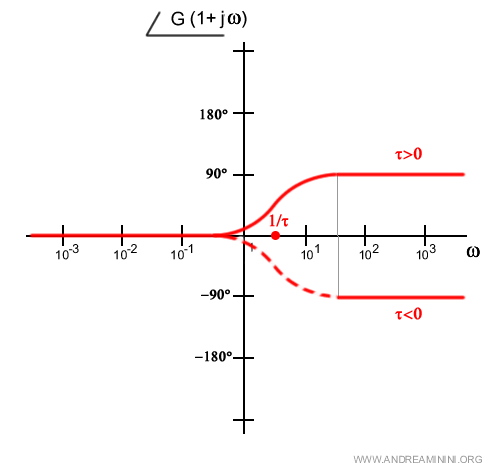
In caso di molteplicità degli zeri superiore a 1, la fase va moltiplicata per la molteplicità h.
$$ φ(ω)=arg(1+jωτ)^h = h \cdot arctg(ωτ) $$
Ad esempio, se h=2 la fase è uguale a 180°.
Il punto di passaggio diventa, invece, 90° in corrispondenza del punto di rottura 1/τ.
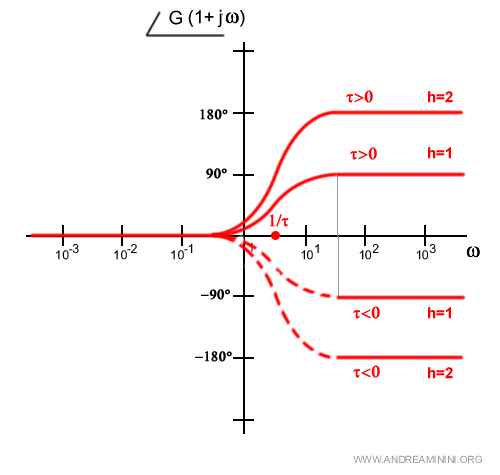
Nota. In modo simile posso tracciare anche la fase del binomio al denominatore. $$ φ(ω)=arg(1+jωτ)^{-1} = \frac{1}{arg(1+jωτ)} = - arctg(ωτ) $$ Se la frequenza ω è molto piccola $$ ω << \frac{1}{|τ|} $$ prevale la parte reale (1) su quella immaginaria (jωτ) $$ φ(ω)=-arg(1) = 0° $$ Se la frequenza ω è molto grande $$ ω >> \frac{1}{|τ|} $$ prevale la parte immaginaria (jωτ) si quella reale $$ φ(ω)=-arg(ωτ) $$ Il risultato dipende dal segno della variabile τ.
Se τ>0 la fase è circa φ(ω)=-90° ( ossia -π/2 ) $$ \lim_{ ω \rightarrow ∞ } - \arctan(ωτ) = -π/2 \:\: con \:\: τ>0 $$ Se τ<0 la fase è circa φ(ω)=90° ( ossia π/2 ) $$ \lim_{ ω \rightarrow ∞ } - \arctan(ωτ) = π/2 \:\: con \:\: τ<0 $$ In questo caso il grafico è uguale al precedente ma ribaltato
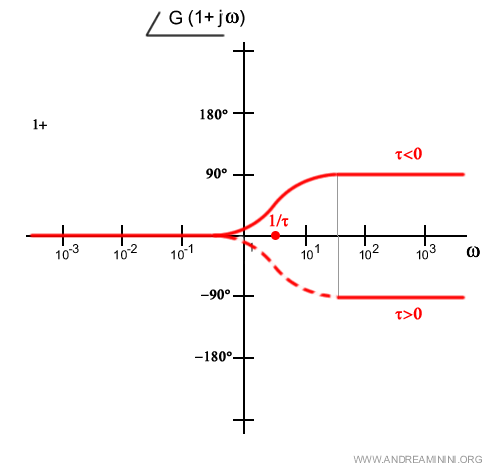
In caso di molteplicità dei poli h<-1 il discorso è analogo a quello fatto per gli zeri ma va ribaltato. $$ φ(ω)=arg(1+jωτ)^{-h} = - h \cdot arctg(ωτ) $$ Ecco un esempio di molteplicità dei poli per h=-1 e h=-2.
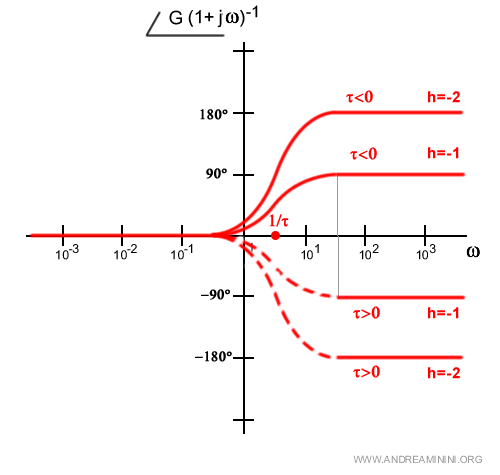
E così via.
