Il trinomio nel diagramma di Bode

Il modulo

Il modulo del fattore trinomio espresso in decibel è

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} | $$

L'unità j è l'unità complessa j=1 e posso ometterla

$$ = 20 \log | 1 + \frac{2ωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} | $$

Ora sostituisco il modulo con la radice quadrata delle potenze dei termini

$$ = 20 \log \sqrt{ 1^2 + ( \frac{2ωδ}{ω_n} )^2 - ( \frac{ω^2}{ω_{n}^2} )^2 } $$

$$ = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

Per studiare il trinomio utilizzo l'analisi asintotica.

In pratica, analizzo il comportamento approssimativo della funzione per gli asintoti ottenuti facendo tendere la variabile indipendente (ω) a zero (0) e a infinito (+∞). Dove ω è la pulsazione.

In questo caso il trinomio è composto da tre variabili: ω, ω_n, δ.

Tolta la variabile indipendente (ω) devo studiare l'impatto dei parametri ω_n (pulsazione naturale) e δ (coefficiente di smorzamento) sul comportamento della funzione.

Per il momento mi concentro sulla pulsazione naturale ω_n, in quanto il parametro appare in due componenti del trinomio.

Calcolo la pulsazione naturale e la indico sul diagramma di Bode.

Nota. La pulsazione naturale ωn è un valore sempre positivo mentre il coefficiente di smorzamento è un valore inferiore a 1. Quindi, l'analisi è molto semplice.

Se ω è molto più piccolo di ω_n, ossia almeno 10 volte più piccolo (una decade)

$$ ω << ω_n $$

I termini dove ω_n appare al denominatore tendono a zero.

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log \sqrt{ 1^2 } $$

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log 1 $$

Il logaritmo di 1 è zero.

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 0 $$

Quindi per valori di ω molto più piccoli di ω_n (fino a una decade prima) la funzione tende a zero.

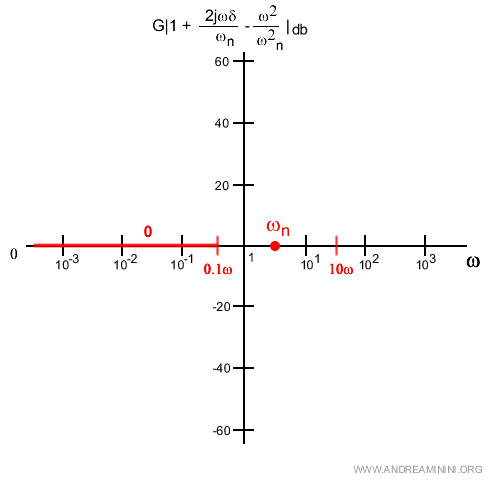
Se ω è molto più grande di ω_n, ossia almeno 10 volte più grande (una decade)

$$ ω >> ω_n $$

I termini dove ω_n appare al denominatore tendono a infinito.

Essendo un'analisi asintotica (approssimativa) prendo il termine più grande ed elimino gli altri.

In questo caso il termine più grande è (ω²/ ω_n²)².

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log \sqrt{ ( \frac{ω^2}{ω_{n}^2} )^2 } $$

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \log \frac{ω^2}{ω_{n}^2 } $$

per la proprietà del logaritmo faccio uscire la potenza

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 20 \cdot 2 \cdot \log \frac{ω}{ω_{n}} $$

$$ | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} |_{dB} = 40 \log \frac{ω}{ω_{n}} $$

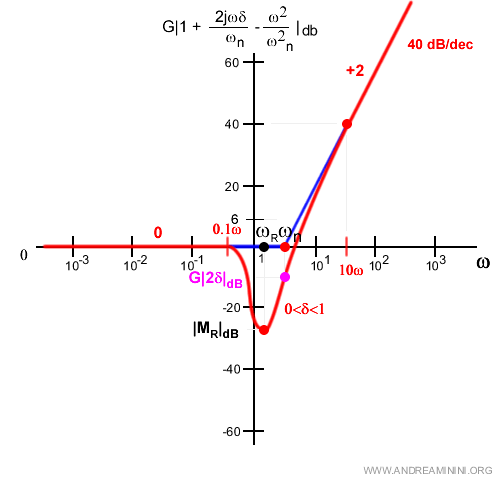
Quindi per valori di ω molto più grandi di ω_n (dopo una decade) la funzione cresce di 40 dB per decade.

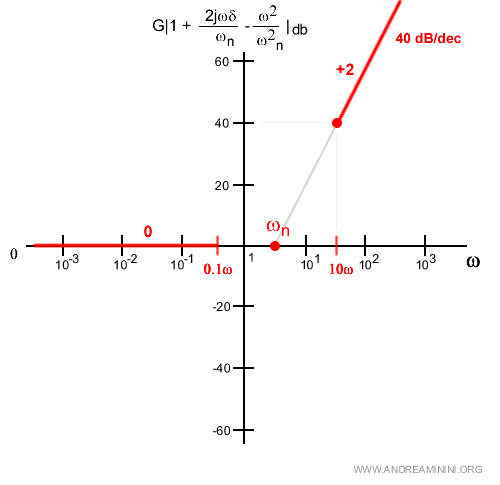
Nota. Il simbolo +2 indica che il grafico cresce di 2·20dB per decade.

Il margine di errore è molto basso prima la decade a sinistra di ω_n e oltre la decade a destra.

L'errore è invece alto nel tratto intermedio ossia nell'intorno di ω_n detto punto di rottura.

Una soluzione semplice e rapida per completare il grafico è unire la pulsazione naturale ω_n tramite due due spezzate.

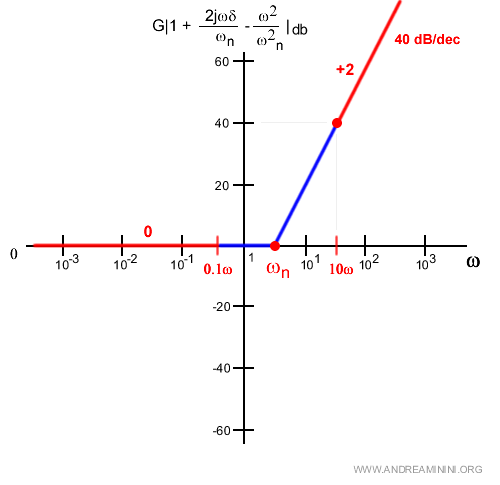
Tuttavia, si tratterebbe di una soluzione approssimativa con margine d'errore troppo elevato nell'intorno di ω_n.

E' quindi necessario studiare in modo più approfondito il comportamento della funzione nel tratto intermedio.

In particolar modo, in questo tratto il comportamento della funzione è influenzato dal coefficiente di smorzamento δ.

Nota. Il coefficiente di smorzamento è compreso δ tra -1 e 1. Tuttavia, essendo elevato al quadrato δ² il suo valore è sempre compreso tra 0 e 1.

Se il coefficiente di smorzamento è δ=1 nel punto di smorzamento ω=ω_n

$$ = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

$$ = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ω}{ω_n} )^2 } $$

Essendo ω=ω_n posso semplificare

$$ = 20 \log \sqrt{ (1-1)^2 + (2)^2 } $$

$$ = 20 \log \sqrt{ 2^2 } $$

$$ = 20 \log 2 $$

Il logaritmo di 2 è 0.3

$$ = 20 · 0.3 = 6 dB $$

Pertanto, nel punto di smorzamento il punto massimo di errore è 6 decibel.

Indico il punto di passaggio nel diagramma di Bode.

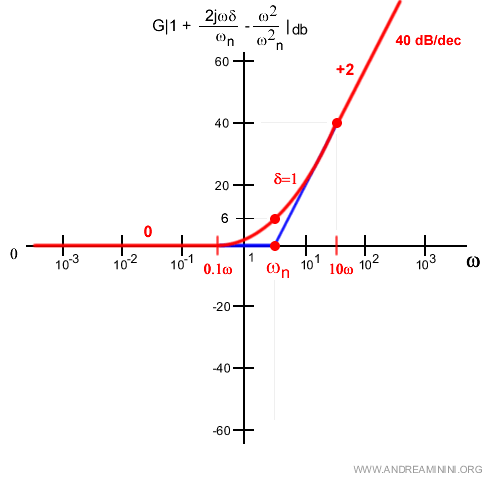
Questa correzione riduce notevolmente il margine di errore nel tratto intermedio rispetto al caso iniziale.

Se il coefficiente di smorzamento è δ=0 nel punto di smorzamento ω=ω_n

$$ = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

$$ = 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 } $$

$$ = 20 \log \sqrt{ (1 - 1 )^2 } $$

$$ = 20 \log \sqrt{ 0 } $$

Il logaritmo di zero è -∞

$$ = 20 \log 0 = -∞ $$

In questo caso si presenta un asintoto verticale negativo.

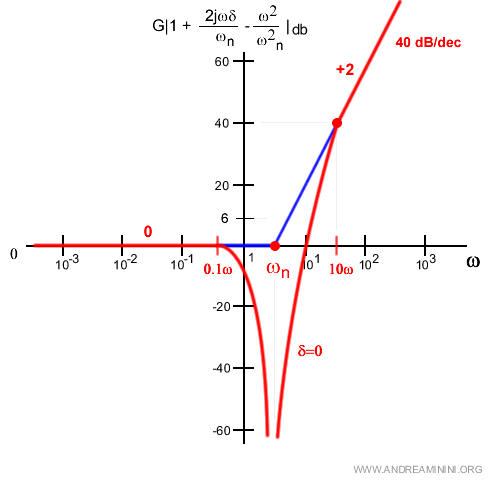
Tra questi due limite δ=1 e δ=0 ci sono infinite situazioni intermedie da studiare con attenzione.

Se il coefficiente di smorzamento è 0<δ<1 nel punto di smorzamento ω=ω_n

$$ 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + ( \frac{2ωδ}{ω_n} )^2 } $$

$$ 20 \log \sqrt{ (1 - \frac{ω^2}{ω_{n}^2} )^2 + \frac{4ω^2δ^2}{ω^2_n} } $$

Per semplicità assegno la variabile u=ω/ω_n

$$ 20 \log \sqrt{ (1 - u^2 )^2 + 4δ^2u^2 } $$

Devo verificare se esiste un punto in cui la funzione raggiunge un minimo detto picco di risonanza

Nota. Quando il picco è un minimo locale, come in questo caso, sarebbe meglio chiamarlo picco di anti-risonanza. Si parla più opportunamente di "picco di risonanza" quando è un massimo locale che in genere si presenta nell'analisi dei poli.

Per farlo calcolo la derivata dell'argomento della funzione rispetto a u e verifico quando è uguale a zero.

$$ D [ (1 - u^2 )^2 + 4δ^2u^2 ] = 0 $$

$$ 2(1 - u^2 ) \cdot (-2u) + 2u \cdot 4δ^2 = 0 $$

$$ -4(1 - u^2 ) u + 8δ^2u = 0 $$

$$ u^2 = 1 - 2δ^2 $$

$$ u = \sqrt{ 1 - 2δ^2} $$

Sapendo che u=ω/ω_n trovo la pulsazione di risonanza

$$ u = \sqrt{ 1 - 2δ^2} $$

$$ \frac{ω}{ω_n} = \sqrt{ 1 - 2δ^2} $$

$$ ω = ω_n \cdot \sqrt{ 1 - 2δ^2} $$

Per maggiore chiarezza indico la pulsazione di risonanza con ω_R

$$ ω_r = ω_n \cdot \sqrt{ 1 - 2δ^2} $$

Poiché 0<δ<1 la radice quadrata sarà un numero compreso tra 0 e 1.

Pertanto la pulsazione di risonanza è inferiore alla pulsazione naturale.

$$ ω_r < ω_n $$

Nel grafico si trova a sinistra del punto di rottura.

Una volta trovata la pulsazione di risonanza (frequenza ω_r) posso facilmente calcolare l'ampiezza ossia il picco di risonanza che ora indico con M_R.

$$ |M_R|_{dB} = 20 \log \sqrt{ (1 - u^2 )^2 + 4δ^2u^2 } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ (1 - (\sqrt{ 1 - 2δ^2} )^2 )^2 + 4δ^2(\sqrt{ 1 - 2δ^2} )^2 } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ (1 - ( 1 - 2δ^2 ) )^2 + 4δ^2( 1 - 2δ^2 ) } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ (1 - 1 + 2δ^2 ) )^2 + 4δ^2( 1 - 2δ^2 ) } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ 4δ^4 + 4δ^2 - 8δ^4 } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ 4δ^2 - 4δ^4 } $$

$$ |M_R|_{dB} = 20 \log \sqrt{ 4δ^2 (1- δ^2) } $$

$$ |M_R|_{dB} = 20 \log ( 2δ \sqrt{ 1- δ^2 } ) $$

Nota. In scala lineare M_R vale $$ M_R = 2δ \sqrt{ 1- δ^2 } $$

A questo punto posso indicare nel diagramma di Bode la frequenza di risonanza e il picco di risonanza.

Poi ridisegnare il grafico nell'intorno della pulsazione naturale.

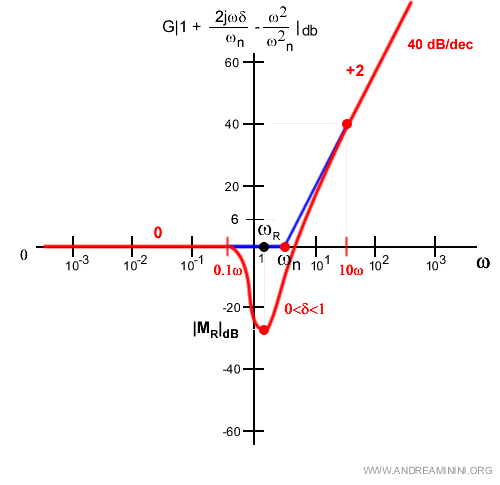
Il legame tra coefficiente di smorzamento e picco di risonanza. Tra il coefficiente di smorzamento δ e il picco di risonanza M_R sono inversamente correlati. Questo grafico mostra il legame. Nel grafico considero il picco di risonanza M_R lineare, non va confuso con la misura in decibel.

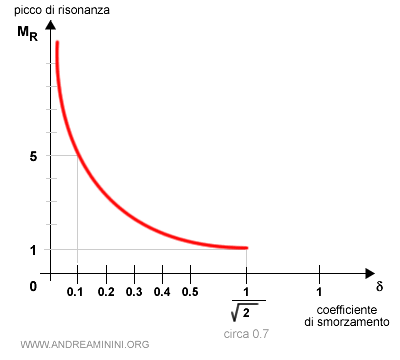
Se δ è compreso tra 0 e 1/√2 (circa 0.7) la curva ha un picco di smorzamento. Viceversa, se δ è compreso tra 1/√2 e 1 non interseca l'asse delle ascisse e non presenta un picco di smorzamento.

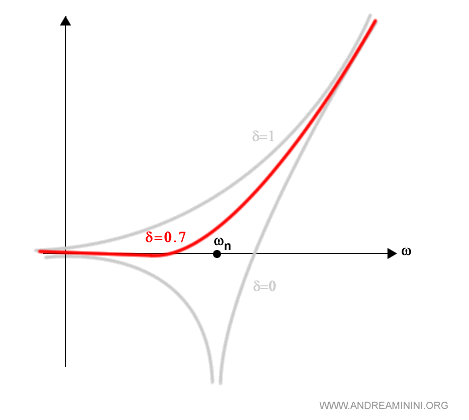
Se δ è uguale a 1/2 ( ossia 0.5 ) allora la curva interseca l'asse dell'ascisse sulla pulsazione naturale ω_n.

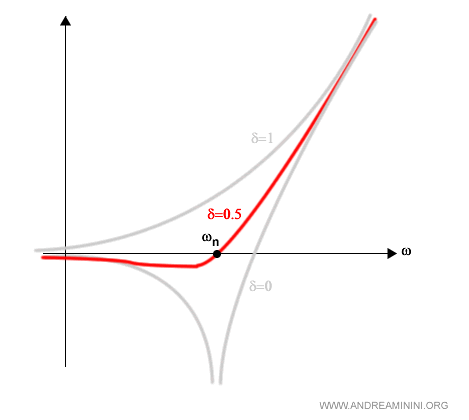
Se δ è compreso nell'intervallo (0-0.5) la curva interseca l'asse dell'ascisse a destra della pulsazione naturale ω_n ed è al di sopra della sua approssimazione asintotica. Quanto più δ si avvicina a zero, tanto più Il picco di smorzamento è marcato e vicino alla pulsazione naturale ω_n.

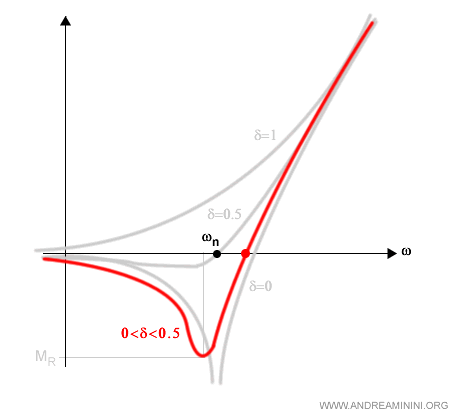
Se δ è compreso nell'intervallo (0.5-0.7) la curva interseca l'asse dell'ascisse a sinistra della pulsazione naturale ω_n.

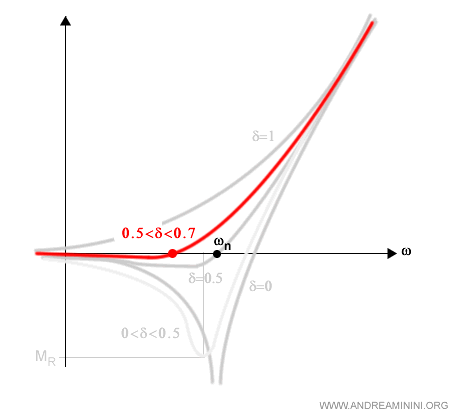
Per un'ulteriore precisione posso anche calcolare l'ampiezza nel punto in cui la pulsazione ω=ω_n ossia u=ω/ω_n=1

$$ |G(jδ)| = 20 \log \sqrt{ (1 - u^2 )^2 + 4δ^2u^2 } $$

$$ |G(jδ)| =20 \log \sqrt{ (1 - 1^2 )^2 + 4δ^2 } $$

$$ |G(jδ)| =20 \log \sqrt{ 4δ^2 } $$

$$ |G(jδ)| =20 \log 2|δ| $$

E' un altro punto di passaggio utile per disegnare il grafico.

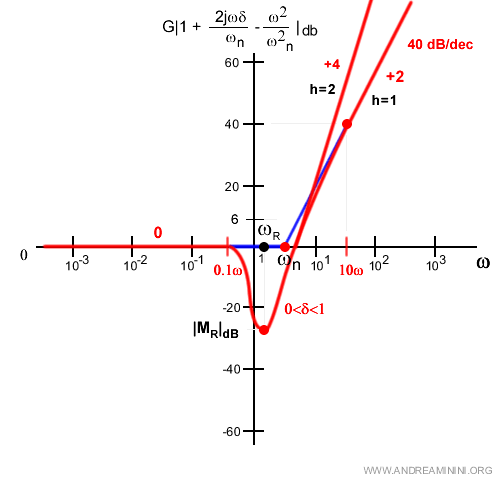
Resta da approfondire la molteplicità.

Fin qui ho ipotezzato la molteplicità pari a 1 ossia h=1.

$$ | ( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} )^h |_{dB} $$

Se fosse h=2 la pendenza del grafico raddoppierebbe passando h 40·db/dec (+2) ossia 80 dB/dec (+4).

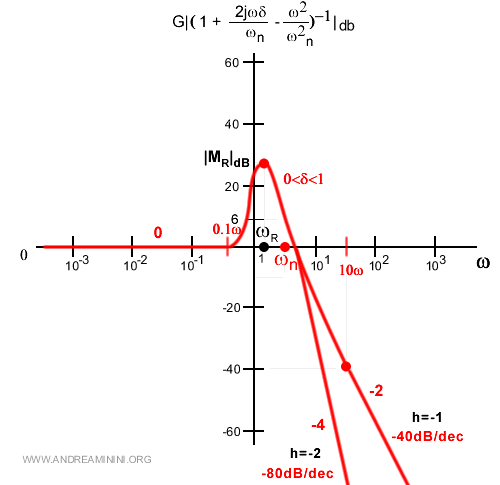
Nota. In modo simile posso tracciare anche il trinomio al denominatore. $$ | ( 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} )^{-1}|_{dB} = 20 \log | \frac{1}{ 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} } | $$ $$ = - 20 \log | 1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2} | $$ In questo caso, a parità di parametri, l'andamento del grafico è opposto al precedente.

La fase

La fase del binomio si calcola in questo modo

$$ φ(ω)=arg(1 + \frac{2jωδ}{ω_n} - \frac{ω^2}{ω_{n}^2}) = arctg( \frac{ \frac{2ωδ}{ω_n} }{1- \frac{ω^2}{ω_n^2}} ) $$

L'arcotangente è il rapporto tra la parte immaginaria (2δω/ω_n) e la parte reale (1-ω²/ω²_n)

In questo caso devo considerare due parametri δ e ω_n. Dove il parametro δ è compreso nell'intervallo (-1, 1) con gli estremi non compresi.

Comincio con il costruire il grafico della fase per valori prossimi allo zero.

L'arcotangente per valori ω tendenti a zero è uguale a zero.

Quindi, fino a una decade prima della pulsazione naturale ω_n la fase è sicuramente nulla.

Poiché il limite dell'arcotangente per ω→∞ è 180 ossia π

$$ \lim_{ω \rightarrow ∞} arctg(ω) = π = 180° $$

Il segno del coefficiente di smorzamento δ influenza il comportamento limite della funzione che può tendere a ±180° una decade dopo ω_n.

$$ \lim_{ω \rightarrow ∞} arctg(ω) = \begin{cases} +180° \:\: se \:\: δ>0 \\ -180° \:\: se \:\: δ<0 \end{cases} $$

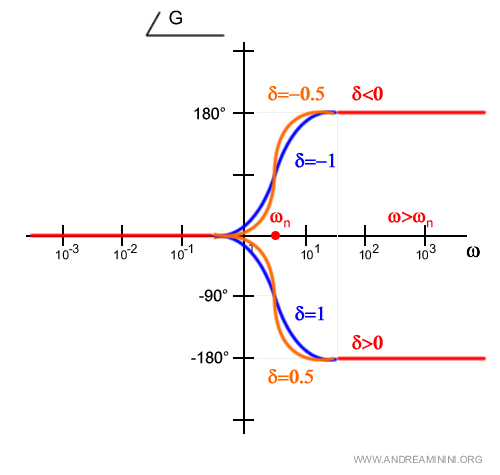
Dal punto di vista grafico

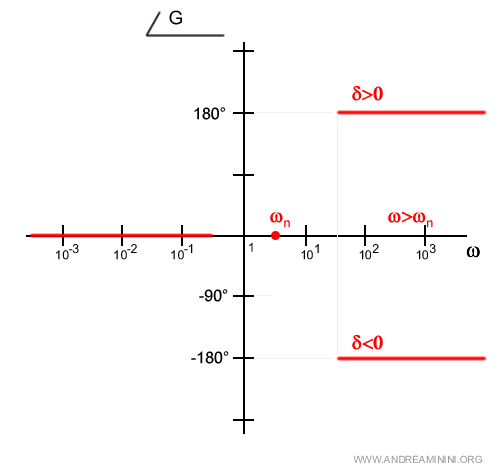
Nel tratto intermedio tra una decade prima e una decade dopo della pulsazione naturale ω_n, il coefficiente di smorzamento δ determina l'andamento del grafico.

Quando δ=0 si ha una spezzata a gradino.

Se δ tende a uno ( δ=1 )

Nel caso limite in cui δ=1 il tratto intermedio intorno alla pulsazione naturale ω_n è addolcito da una curva a S con un punto di flesso a -90° in corrispondenza di ω_n.

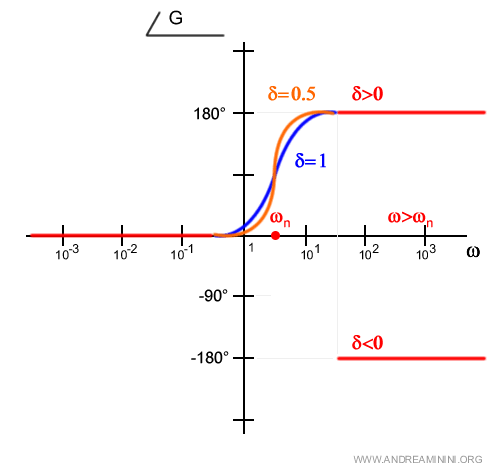
Per i valori intermedi 0<δ<1 si hanno curve meno accentuate con il punto di flesso sempre a -90°.

Se δ tende a meno uno ( δ=-1 )

Nel caso limite in cui δ=1 il segno dell'arcotangente è opposto rispetto al caso (δ=1) e la fase tende a -180°.

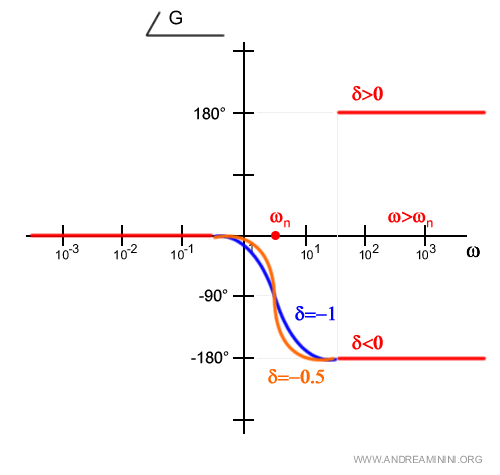
Per il resto valgono le stesse considerazioni.

• Se il coefficiente di smorzamento tende a meno uno (δ=-1) nell'intorno della pulsazione naturale ω_n si ha una curva con punto di flesso a +90° in corrispondenza di ω_n.
• Se invece il coefficiente di smorzamento è negativo ma tende a zero, il tratto intermedio assume più una forma a gradino.

In qualsiasi caso, una decade dopo ω_n la fase è +180° ossia π.

Pertanto, il diagramma complessivo del trinomio è

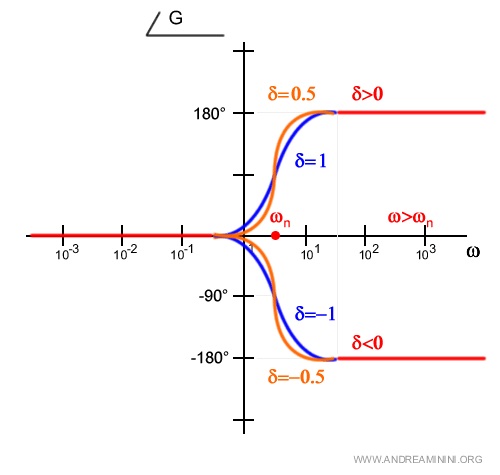
Nota. In modo simile posso tracciare il trinomio al denominatore. $$ φ(ω)=arg(1 + \frac{2jω}{ω_n} - \frac{ω^2}{ω_{n}^2})^{-1} = -arctg( \frac{ \frac{2ω}{ω_n} }{1- \frac{ω^2}{ω_n^2}} ) $$ In questo caso però c'è un segno meno davanti all'arcotangente che ne ribalta il segno. $$ \lim_{ω \rightarrow ∞} -arctg(ω) = -π = -180° $$ Quindi se il coefficiente di smorzamento δ>0 la fase è -180° mentre se δ<0 la fase è +180°.

E così via.