La teoria dei quanti

La teoria dei quanti fu introdotta nel 1900 dal fisico tedesco Max Planck, per spiegare la distribuzione delle radiazioni elettromagnetiche emesse da un corpo nero, cioè da un corpo ideale capace di assorbire e riemettere tutta la radiazione incidente.

Planck ipotizzò che l’energia non fosse emessa in maniera continua, come si pensava fino ad allora, ma in “pacchetti” discreti, chiamati quanti di energia. L’energia di ciascun quanto è proporzionale alla frequenza della radiazione:

$$ E = h \cdot \nu $$

Dove $h$ è la costante di Planck.

Questo processo prende il nome di quantizzazione. In altre parole, un sistema fisico non può assumere valori energetici qualsiasi, ma solo multipli interi di un’unità fondamentale.

Cosa significa quantizzare? Per capire il concetto, possiamo usare delle analogie. Le dune del deserto: a occhio nudo sembrano masse continue di sabbia, ma in realtà sono composte da miliardi di granelli, unità discrete. Allo stesso modo, ciò che in natura ci sembra continuo (es. l’energia della radiazione, il moto degli elettroni, le vibrazioni atomiche) a livello microscopico risulta quantizzato.

La stessa fotografia a prima vista appare come un’immagine continua, ma ingrandendola scopriamo che è formata da una griglia di puntini luminosi (pixel).

Perché Planck propose il quanto?

All’inizio del ’900 gli scienziati sapevano che l’energia emessa da un corpo caldo dipende dalla sua temperatura.

Per studiare il fenomeno in modo ideale, introdussero il concetto di corpo nero, un oggetto capace di assorbire e riemettere tutta la radiazione incidente, indipendentemente dal materiale di cui è fatto.

Le misurazioni mostrarono che, per ogni temperatura assoluta $T$, l’energia emessa $ E(λ) $ si distribuisce tra le varie lunghezze d’onda $\lambda$ secondo una curva caratteristica, con un picco massimo che si sposta al variare della temperatura.

Queste curve hanno una forma tipica "a campana".

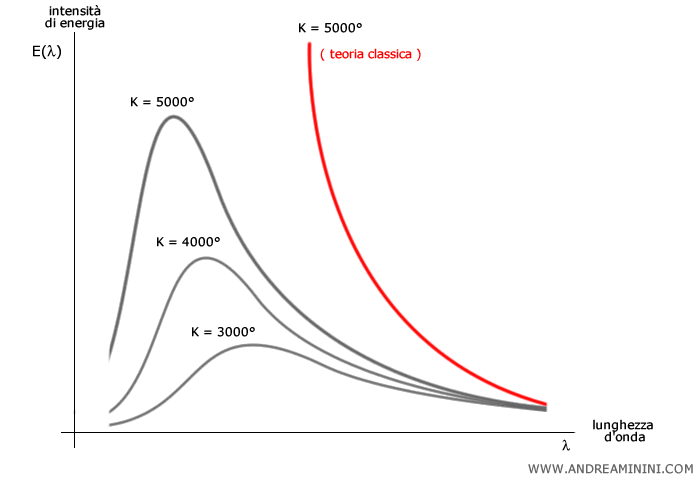
La fisica classica però non riusciva a descrivere questo andamento. Le leggi dell’elettromagnetismo prevedevano infatti che un corpo nero emettesse radiazione in modo continuo a tutte le frequenze, con un’intensità crescente all’aumentare della frequenza.

Questa previsione portava alla cosiddetta catastrofe ultravioletta: un risultato assurdo, secondo cui un corpo nero dovrebbe emettere energia infinita alle alte frequenze.

Alcune leggi classiche rimanevano comunque valide: ad esempio, la legge di Stefan-Boltzmann stabiliva che la potenza totale emessa da un corpo nero è proporzionale alla quarta potenza della sua temperatura:

$$ E = \sigma T^4 $$

Dove $\sigma$ è la costante di Stefan-Boltzmann.

Il problema aperto era spiegare come l’energia si distribuisce tra le diverse lunghezze d’onda.

Per risolvere questo enigma, Max Planck propose un’idea rivoluzionaria: l’energia elettromagnetica non è continua, ma suddivisa in pacchetti discreti, i quanti. E qui entra in gioco la costante di Max Planck.

Cos'è la costante di Planck?

Se l’energia è quantizzata, significa che non può assumere valori qualsiasi, ma solo multipli interi di un’unità fondamentale.

Secondo Planck, l’energia associata a una radiazione elettromagnetica di frequenza $\nu$ è data dalla relazione:

$$ E = h \nu $$

Dove:

• $E$ è l’energia di un quanto,
• $\nu$ è la frequenza della radiazione
• $h$ è la costante di Planck, pari a circa $6{,}626 \times 10^{-34} \, \mathrm{J \cdot s}$.

La costante $h$ è quindi una costante universale che stabilisce la dimensione minima con cui l’energia può essere “impacchettata”. Non è un quanto essa stessa, ma il fattore che lega il quanto di energia alla frequenza della radiazione.

Dalla formula semplice alla legge di Planck

Planck riuscì, grazie a questa ipotesi, a formulare l’equazione che descrive la distribuzione spettrale dell’energia emessa da un corpo nero.

$$ E(\nu) = \frac{8 \pi h \nu^3}{c^3} \cdot \frac{1}{e^{h\nu/kT}-1} $$

dove  $c$ è la velocità della luce, $k$ è la costante di Boltzmann,  $T$ è la temperatura assoluta.

Questa legge spiega perfettamente la forma “a campana” delle curve di emissione, evitando la catastrofe ultravioletta prevista dalla fisica classica.

Inoltre, la legge di Planck interpola correttamente i due limiti: legge di Rayleigh - Jeans (basse frequenze) e legge di Wien (alte frequenze).

In conclusione, la costante di Planck segna il confine tra la fisica classica e la fisica quantistica: al di sotto di questa scala, i fenomeni non sono più continui, ma quantizzati.

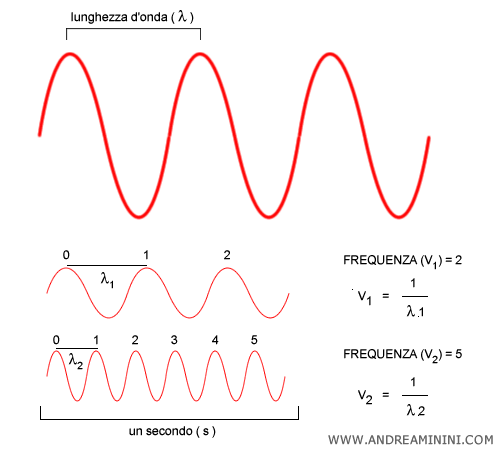
La differenza tra frequenza e lunghezza d'onda. La frequenza $\nu$ e la lunghezza d’onda $\lambda$ sono due modi diversi di descrivere la stessa onda: $$ c = \lambda \nu $$ La frequenza ($\nu$) indica quante oscillazioni avvengono in un secondo. La lunghezza d’onda ($\lambda$), invece, è la distanza tra due creste successive. Al crescere della frequenza, la lunghezza d’onda diminuisce, e viceversa.

Per capire questa scala microscopica delle grandezze fisiche è sufficiente analizzare l'azione di un elettrone quando gira intorno al nucleo dell'atomo di idrogeno seguendo un’orbita circolare attorno al nucleo ( 2πr ).

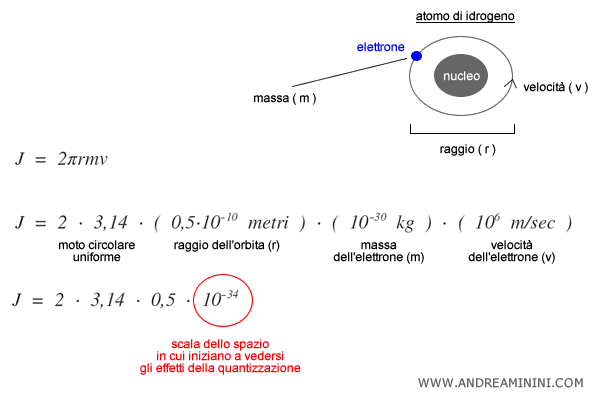
Per un elettrone di massa $m \approx 9,1 \times 10^{-31}\,\text{kg}$, raggio orbitale $r \approx 0,5 \times 10^{-10}\,\text{m}$ e velocità $v \approx 10^6\,\text{m/s}$, il momento angolare vale:

$$ J = 2 \pi r m v \sim 10^{-34} \, \text{J·s} $$

Questo valore coincide con l’ordine di grandezza della costante di Planck $h$.

È dunque a questa scala che la meccanica classica cessa di essere valida e diventa necessario introdurre la quantizzazione dei livelli energetici (modello di Bohr, meccanica quantistica).

La differenza tra quanti e onde elettromagnetiche

Nella teoria classica dell’elettromagnetismo, una radiazione luminosa viene descritta come un’onda che distribuisce la propria energia in modo continuo su tutto lo spettro delle frequenze.

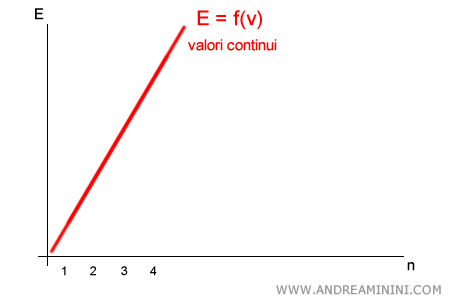
Secondo Planck, invece, l’energia non è continua: può assumere soltanto valori discreti, multipli di un quanto elementare $h\nu$. In altre parole:

$$ E = n \cdot h\nu \qquad (n = 1,2,3,\dots) $$

Tra $1 \cdot h\nu$ e $2 \cdot h\nu$ non esistono valori intermedi: il sistema può emettere o assorbire solo un numero intero di quanti.

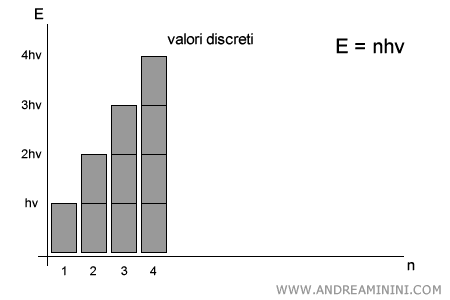
Questa visione porta a considerare la luce non solo come un’onda, ma anche come un flusso di particelle, chiamate fotoni, ciascuno con energia $h\nu$.

Tuttavia la descrizione ondulatoria non viene abbandonata: entrambe le immagini (onda e particella) restano valide.

Il dualismo onda-particella

Gli sviluppi successivi della meccanica quantistica portarono alla conclusione che la radiazione elettromagnetica possiede una doppia natura:

• in alcuni esperimenti manifesta un comportamento ondulatorio (interferenza, diffrazione)
• in altri un comportamento corpuscolare (effetto fotoelettrico, urto con elettroni)

Questo fenomeno è noto come "dualismo onda-particella". Entrambi gli aspetti coesistono e si manifestano a seconda dell’esperimento.

E non riguarda solo la luce: anche gli elettroni, i protoni e i neutroni mostrano proprietà ondulatorie, come dimostrato dagli esperimenti di diffrazione degli elettroni.

L'effetto fotoelettrico

L’ipotesi dei quanti proposta da Planck nel 1900, nata per spiegare lo spettro di emissione del corpo nero, si rivelò ben presto utile anche in altri contesti inattesi.

Nel 1905 Albert Einstein applicò il concetto di quanto allo studio dell’effetto fotoelettrico, un fenomeno osservato già alla fine dell’Ottocento: quando la luce colpisce la superficie di un metallo, da essa vengono emessi elettroni.

Secondo l’elettromagnetismo classico, l’energia trasportata dalla luce dipende solo dalla sua intensità, cioè dall’ampiezza dell’onda.

Pertanto, una luce molto intensa, indipendentemente dal colore, avrebbe dovuto fornire energia sufficiente a strappare elettroni dal metallo. Ma gli esperimenti mostravano un risultato diverso:

• se la frequenza ( $ \nu $ ) della luce è troppo bassa (ad esempio luce rossa), non si osserva alcuna emissione di elettroni, anche aumentando l’intensità;
• se invece la frequenza ( $ \nu $ ) è superiore a una certa soglia (ad esempio luce ultravioletta), anche un fascio debole riesce a estrarre immediatamente elettroni.

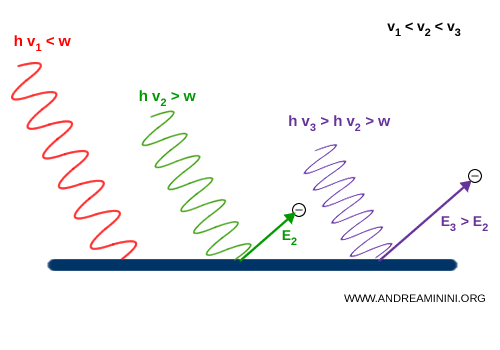
Einstein spiegò il fenomeno introducendo l’ipotesi che la luce fosse composta da quanti di energia (oggi chiamati fotoni), particelle elementari di energia quantizzata:

$$ E = h \nu $$

Un fotone, urtando la superficie del metallo, può trasferire la propria energia a un elettrone.

Se questa energia è sufficiente a superare la funzione lavoro $ W $ (l’energia minima necessaria a liberare un elettrone dal metallo), l’elettrone viene emesso. In caso contrario, non accade nulla, a prescindere dall’intensità della luce.

$$ E_{cin} = h \nu - W $$

Questa spiegazione confermò che la radiazione elettromagnetica ha una natura corpuscolare, oltre a quella ondulatoria.

Nota. Per questo lavoro Einstein ricevette il Premio Nobel per la Fisica nel 1921, e l’effetto fotoelettrico divenne una delle prove decisive della teoria dei quanti.

Il modello atomico di Bohr

Nel 1913 Niels Bohr propose un nuovo modello dell’atomo per risolvere le contraddizioni emerse con la fisica classica.

Secondo la teoria elettromagnetica tradizionale, un elettrone che orbita attorno al nucleo avrebbe dovuto emettere continuamente energia e cadere rapidamente nel nucleo stesso: un atomo instabile, quindi impossibile.

Bohr introdusse un’idea radicale: gli elettroni non possono occupare orbite qualsiasi, ma soltanto determinate orbite stazionarie, corrispondenti a livelli energetici discreti. In queste orbite l’elettrone non irradia energia, e l’atomo rimane stabile.

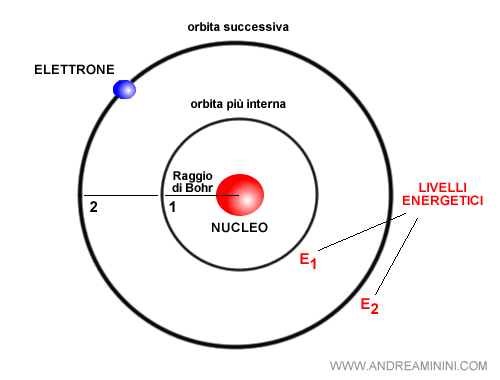
Quando un elettrone passa da un livello a un altro, l’atomo emette o assorbe un fotone con energia pari alla differenza tra i due livelli: $ E = h \nu $

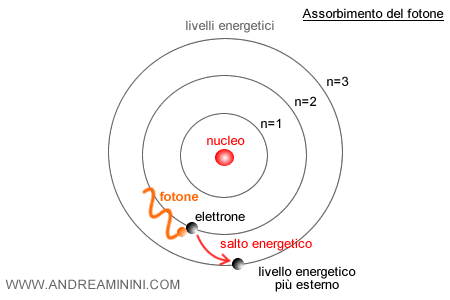
In questo modo Bohr riuscì a spiegare con precisione lo spettro di emissione dell’idrogeno, riproducendo la sequenza delle sue righe spettrali.

Il contributo di Bohr fu decisivo perché integrò la nozione di quanto di energia (introdotta da Planck ed Einstein) all’interno della struttura atomica, segnando un passaggio fondamentale verso la meccanica quantistica.

Dalla teoria dei quanti alla meccanica quantistica

Negli anni successivi l’ipotesi quantistica fu estesa ad altri fenomeni: l’ipotesi delle onde di materia di de Broglie (1924), la meccanica ondulatoria di Schrödinger e la meccanica matriciale di Heisenberg (1925-26).

• Ipotesi delle onde di materia di de Broglie (1924)
  Louis de Broglie propose che non solo la luce, ma anche le particelle materiali (come elettroni e protoni) potessero comportarsi come onde. A ogni particella di quantità di moto $p$ è associata una lunghezza d’onda: $$ \lambda = \frac{h}{p} $$  Questa intuizione estese il dualismo onda-particella dalla radiazione elettromagnetica alla materia stessa.
• Meccanica matriciale di Heisenberg (1925)
  Werner Heisenberg, partendo dai dati sperimentali sugli spettri atomici, elaborò una descrizione matematica basata sulle matrici anziché su traiettorie o onde visibili. In questo formalismo, le grandezze fisiche sono operatori che obbediscono a particolari regole di commutazione, da cui nasce anche il principio di indeterminazione. Poco dopo, Born e Jordan svilupparono formalmente il metodo matriciale insieme a lui (Born - Jordan - Heisenberg paper). Pur molto astratta, questa formulazione si rivelò equivalente a quella di Schrödinger e contribuì a gettare le basi della meccanica quantistica moderna.
• Meccanica ondulatoria di Schrödinger (1926)
  Erwin Schrödinger formulò un’equazione matematica capace di descrivere l’evoluzione temporale della funzione d’onda $\psi$, che contiene tutta l’informazione sullo stato quantistico di un sistema. In questo quadro, l’elettrone non è più visto come una particella che orbita attorno al nucleo, ma come un’onda di probabilità distribuita nello spazio. Le soluzioni stazionarie dell’equazione spiegano i livelli energetici discreti degli atomi. L'equazione di Schrödinger fu il primo articolo sulla meccanica ondulatoria. Nei mesi successivi venne dimostrato che la sua formulazione era equivalente a quella di Heisenberg.
• La funzione d'onda di Max Born (1926)
  Max Born introdusse l’interpretazione probabilistica della funzione d’onda $|\psi|^2$ come densità di probabilità. Senza questa, la meccanica ondulatoria sarebbe rimasta matematica elegante ma fisicamente poco chiara.
• Il principio di indeterminazione di Heisenberg (1927)
  Heisenberg formulò il principio di indeterminazione ($\Delta x \cdot \Delta p \geq \hbar/2$), che chiarì il significato fisico della nuova teoria.
• Paul Dirac e l’unificazione (1926 - 1928)
  Paul Dirac svolse un ruolo cruciale sia nel dimostrare l’equivalenza formale tra la meccanica matriciale di Heisenberg e quella ondulatoria di Schrödinger, sia nel formulare nel 1928 la sua celebre equazione relativistica dell’elettrone. Quest’ultima univa la meccanica quantistica con la relatività ristretta e prevedeva in modo naturale l’esistenza dell’antiparticella dell’elettrone: il positrone, scoperto sperimentalmente pochi anni dopo da Anderson (1932).
• Conferenza di Solvay (1927)
  Si tenne a Bruxelles nell’ottobre del 1927 sul tema "Elettroni e fotoni", cioè sui fondamenti della meccanica quantistica che era appena nata. Parteciparono i più grandi fisici del tempo: Planck, Einstein, Bohr, Heisenberg, Schrödinger, Dirac, Born, Pauli, De Broglie, Lorentz... insomma, quasi tutti i fondatori della fisica moderna erano nella stessa stanza. La famosa foto di gruppo mostra 29 partecipanti, di cui ben 17 erano o sarebbero diventati Premi Nobel.
  
  La Conferenza di Solvay sancì il trionfo della meccanica quantistica: le idee di Bohr, Heisenberg, Schrödinger e Born furono accettate come la nuova base della fisica. Nello stesso periodo Dirac stava elaborando la sua teoria relativistica dell’elettrone (1928), che avrebbe completato il quadro. Da quel momento, la fisica classica rimase valida solo come approssimazione macroscopica, mentre la fisica quantistica divenne la teoria fondamentale del mondo microscopico.

  Lo scontro Einstein - Bohr. Einstein non accettava l’interpretazione probabilistica introdotta da Born e difesa da Bohr e Heisenberg. Celebre la sua frase: "Dio non gioca a dadi con l’universo". D'altra parte, Bohr ribatteva che non era compito della fisica dire a Dio cosa fare, difendendo l’interpretazione probabilistica (poi detta "interpretazione di Copenaghen"). Si aprì così il grande dibattito filosofico sulla natura della realtà quantistica, che sarebbe proseguito per decenni.

• Verso la teoria quantistica dei campi (anni ’30 - ’40)
  Dopo la meccanica quantistica "non relativistica", i fisici svilupparono una versione relativistica e di campo, dando origine alla meccanica quantistica relativistica e poi all’elettrodinamica quantistica (QED). Questa teoria descrive la radiazione elettromagnetica come campo quantizzato e le interazioni tra elettroni, positroni e fotoni con estrema precisione. La QED aprì la strada alle teorie delle interazioni fondamentali, la cromodinamica quantistica (QCD) e il modello standard, e rappresenta uno dei primi esempi riusciti di teoria quantistica dei campi.

Dall’intreccio di queste idee nacque la meccanica quantistica, una nuova teoria fisica che, a partire dagli anni ’20, rivoluzionò la comprensione del mondo microscopico.

Quindi, Il passaggio dalla teoria dei quanti alla meccanica quantistica non fu opera di un singolo autore, ma il risultato di un percorso collettivo a cui contribuirono molti scienziati con ruoli decisivi.

E così via.