Il corpo nero
Un corpo nero è un oggetto ideale che:
- assorbe tutta la radiazione elettromagnetica incidente, indipendentemente dalla frequenza o dalla direzione, senza rifletterla all'esterno.
- emette radiazione termica con uno spettro che dipende solo dalla sua temperatura assoluta, e non dalla sua composizione chimica o superficie.
Queste due proprietà, assorbimento totale ed emissione dipendente solo dalla temperatura, lo rendono un modello teorico ideale per studiare le leggi della radiazione.
In altre parole, è un assorbitore ideale e un emettitore ideale.
Nota. Non esiste fisicamente un corpo nero perfetto. La sua definizione non nasce per descrivere un oggetto, ma per rendere conto dell’insufficienza della fisica classica a spiegare la radiazione termica.
La spiegazione
In genere, è rappresentato come un oggetto cavo che comunica con l'esterno tramite un foro.
Quando le radiazioni entrano nella cavità, si riflettono sulle pareti interne restando intrappolate e, infine, sono assorbite dal corpo.

Ogni volta che la radiazione colpisce la parete, una parte viene assorbita sotto forma di energia termica e la restante parte viene riflessa.
Dopo molti rimbalzi, quasi tutta l’energia viene assorbita dalle pareti interne. La probabilità che la radiazione incidente rimbalzi e riesca a uscire dal foro è trascurabile. Il foro appare nero.
L’energia della radiazione incidente aumenta l’agitazione termica degli elettroni nelle pareti interne e viene trasformata in calore, portando il corpo a una nuova temperatura interna $T$.
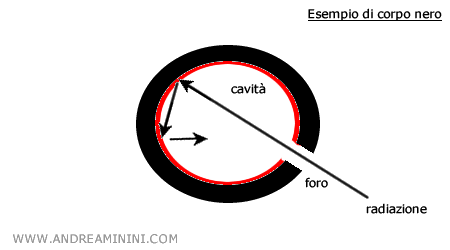
Pertanto, le pareti del corpo nero iniziano a emettere spontaneamente nuova radiazione con uno spettro che dipende solo dalla temperatura $T$ del corpo e non dalla radiazione entrata.
Parte di questa nuova radiazione resta nella cavità (creando un equilibrio interno), e una piccola parte fuoriesce dal foro.
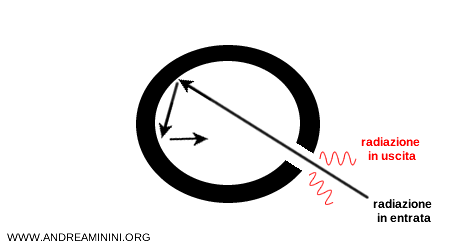
Quindi, il foro si comporta come una sorgente ideale di radiazione termica.
Nel caso ideale di equilibrio termico:
- la radiazione in entrata è la radiazione assorbita
- la radiazione assorbita è la la radiazione emessa
Complessivamente, l'energia totale nel sistema rimane costante.
Questo stato si chiama equilibrio radiativo.
La frequenza delle radiazioni elettromagnetiche emesse dal corpo nero è determinata esclusivamente dalla temperatura del corpo e non anche dalle radiazioni riflesse o dal materiale con cui è costruito il corpo.
In questo modo, sottoponendo al corpo una temperatura diversa si possono studiare tutte le frequenze dello spettro delle radiazioni elettromagnetiche in uscita.
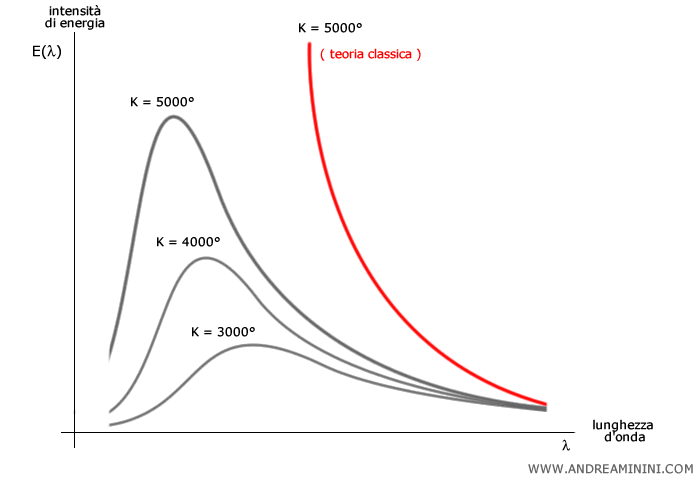
In conclusione, per ogni temperatura (K) esiste un particolare spettro di frequenza e una distribuzione dell'intensità di energia E(λ) emessa dal corpo nero, ossia una determinata curva della lunghezza d'onda.
Da cosa dipende la temperatura di equilibrio $ T $ di un corpo nero? La temperatura di equilibrio di un corpo nero dipende dalla potenza assorbita per unità di superficie (in Watt), ovvero dalla quantità di energia assorbita ogni secondo per metro quadrato. La lunghezza d’onda $\lambda$ della radiazione incidente (ad esempio luce rossa, blu, IR, UV) determina l’energia di ciascun fotone secondo la relazione $E = h\nu$, ma non basta a stabilire la potenza totale: questa dipende anche da quanti fotoni vengono assorbiti ogni secondo. A parità di lunghezza d’onda, un fascio più intenso (cioè con maggiore potenza) trasferisce più energia, e il corpo nero raggiunge una temperatura maggiore per ristabilire l’equilibrio radiativo.
Un corpo nero non è “nero” nel senso visivo comune
Se è freddo, non emette luce visibile ed appare effettivamente nero.
Ma aumentando la temperatura, comincia a emettere radiazione:
- A temperatura ambiente, l’emissione è nell’infrarosso (invisibile all’occhio umano);
- A temperature maggiori, la radiazione si sposta nel visibile:
- Rosso (800 - 1000 K)
- Arancione-giallo (2000 - 3000 K)
- Bianco (oltre 5000 K), come nel caso del Sole.
Nota. Il Sole è approssimabile come un corpo nero a 5778 K. Il suo spettro visibile corrisponde alla luce bianca con massima emissione nel visibile. In astrofisica, si assume spesso che le stelle si comportino come corpi neri per determinare temperatura e colore.
Il corpo nero nella fisica classica
Nel '800 gli scienziati si accorsero di queste due caratteristiche del corpo nero e formularono diverse leggi fisiche, tra cui la legge Stefan-Boltzmann e la legge di Wien.
Nota. La legge di Stefan-Boltzmann individua la relazione tra l'energia ( E ) emessa dal corpo nero e la sua temperatura ( T ). La legge di Wien, invece, quella tra la lunghezza d'onda ( λ ) di massima emissione energetica E( λ )max e la temperatura del corpo ( T ).
Tuttavia, gli scienziati del XIX secolo non riuscivano a spiegare con le leggi classiche della fisica l'andamento della curva dello spettro elettromagnetico del corpo nero.
Nella teoria fisica classica le radiazioni erano composte esclusivamente da onde elettromagnetiche e la misura del fenomeno si basava su grandezze continue.
Il corpo nero nella fisica quantistica
Il primo a fornire una spiegazione all'andamento dello spettro elettromagnetico del corpo nero fu Max Planck all'inizio del '900. La sua spiegazione, però, si basava su un concetto particolarmente innovativo, al punto da creare un nuova meccanica fisica.
Secondo Planck, la radiazione elettromagnetica era composta da corpuscoli o particelle elementari, detti quanti, che veicolavano una determinata energia in base alla frequenza della radiazione.
Questo rese possibile misurare l'energia come una grandezza discreta secondo quantità multiple del quanto e spiegare matematicamente la forma a U rovesciata della curva dell'energia.
La teoria dei quanti di Planck fu il punto di partenza su cui venne costruita la teoria della fisica quantistica.
