Supervisore del sistema a eventi discreti
Cos'è il supervisore
Il supervisore è la componente di controllo di un sistema a eventi discreti (SED) con controllo supervisivo. Si occupa di abilitare o disabilitare gli eventi o gli stati, per soddisfare le specifiche di controllo del sistema.
Le specifiche di controllo sono regole riguardanti l'abilitazione degli stati e degli eventi del sistema.
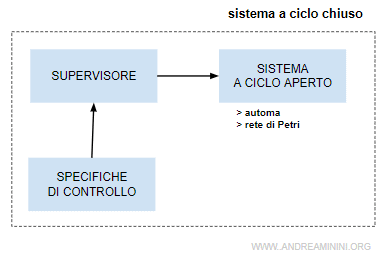
A cosa serve il supervisore
Il supervisore è usato per introdurre il controllo e la retroazione, tipici dei sistemi ad avanzamento temporale SAT, nei sistemi a eventi discreti SED (automi, reti di Petri, ecc. ).
Come funziona il supervisore
Il supervisore è composto da una funzione di controllo che genera degli ingressi di controllo a partire dal linguaggio dell'automa
$$ f: L \rightarrow ξ $$
In base alla sequenza di eventi w dell'automa, la funzione genera un ingresso di controllo contenente gli eventi attivi non controllabili e gli eventi controllabili abilitati.
L'ingresso di controllo contiene gli eventi che possono verificarsi dopo la sequenza di eventi w.
La differenza tra eventi attivi e abilitati. Un evento attivo è un evento che può verificarsi a partire da un determinato stato. E' controllabile se il supervisore può abilitarlo o disabilitarlo. Viceversa, è non controllabile. Gli eventi non controllabili sono sempre attivi. Gli eventi controllabili sono attivi solo se abilitati.
La funzione di controllo f() può essere nel dominio degli eventi (w) o degli stati (x).
Nel primo caso si parla di specifiche dinamiche (eventi) mentre nel secondo di specifiche statiche (stati).
In genere si preferisce usare la funzione di controllo nel dominio degli eventi f(w) perché è più generale e versatile.
Nota. Qualsiasi specifica statica sugli stati f(x) può essere realizzata tramite una specifica dinamica sugli eventi f(w). Viceversa, non vale il contrario. Non tutte le specifiche dinamiche sugli eventi f(w) possono essere realizzate tramite le specifiche statiche sugli stati f(x).
Pertanto, la funzione di controllo f(w) deve essere applicata a ogni parola w, ossia per ogni sequenza di eventi dell'automa.
Un esempio pratico
Dopo la sequenza w=ac l'automa si trova nello stato x2.
Gli eventi attivi nello stato x2 sono A(x2)={d,e}.
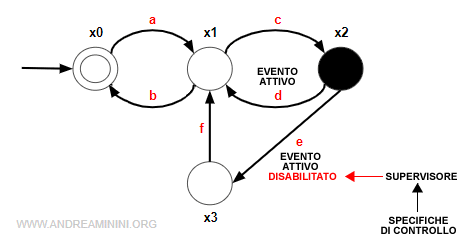
Tuttavia, l'evento "e" è disabilitato dal supervisore. Quindi, l'automa può selezionare soltanto l'evento "d".
Pertanto l'ingresso di controllo dopo la sequenza w=ac è
$$ ξ(ac) = \{ d \} $$
Se l'evento "e" fosse abilitato dal supervisore, l'ingresso di controllo dopo la sequenza w=ac sarebbe
$$ ξ(ac) = \{ d,e \} $$
In questo caso, l'automa potrebbe selezionare "d" oppure "e" come prossimo evento dallo stato x2.
La differenza tra eventi controllabili e non controllabili. Non tutti gli eventi sono controllabili dal supervisore. In genere, gli eventi controllabili sono indicati con il simbolo dei due punti vicino alla lettera. Il supervisore può abilitare o disabilitare soltanto gli eventi controllabili. Gli eventi non controllabili sono comunque attivi. Ad esempio, in questo automa gli eventi controllabili sono soltanto Ec={f,e} mentre gli altri Enc={a,b,c,d} non sono controllabili dal supervisore.
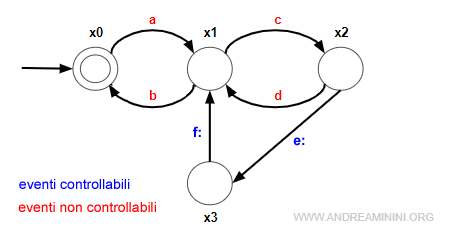
Per ogni sequenza di eventi (w) il supervisore determina un ingresso di controllo che limita gli eventi attivi dell'automa.
Posso rappresentare il supervisore in forma tabellare.
Ad esempio, in questa specifica il supervisore disabilita l'evento "e".
Il supervisore abilita l'evento "e" quando l'evento "c" si verifica almeno due volte.
| w | x | ξ(w) |
|---|---|---|
| ε | x0 | ξ(abcdf) |
| a | x1 | ξ(abcdf) |
| ac | x2 | ξ(abcdf) |
| acd | x1 | ξ(abcdf) |
| acdc | x2 | ξ(abcdef) |
| ... |
Questa rappresentazione va bene per piccoli processi. Non è praticabile per processi e automi complessi.
E' quindi preferibile ridurre le specifiche a semplici regole di sistema.
$$ \begin{cases} f(w) = ξ(abcdef) \:\: se \:\: w=(acdc)^n \\ f(w) = ξ(abcdef) \:\: se \:\: w=(acdc)^nef \\ f(w) = ξ(abcdf) \:\: \text{ negli altri casi } \end{cases} $$
In alternativa, posso rappresentarlo con una rappresentazione sistema.
La supervisione sistema
Posso rappresentare il supervisore come un sistema SED a se stante (grafo del supervisore) che affianca l'automa e introduce alcune regole di evoluzione (specifiche di controllo).
Nel grafico del supervisore replico la stessa sequenza di eventi w del primo sistema (automa).
Esempio
L'evento "e" viene abilitato dal supervisore quando l'evento "c" si verifica due volte.
Tra il primo evento e il secondo "c" possono verificarsi altri eventi.
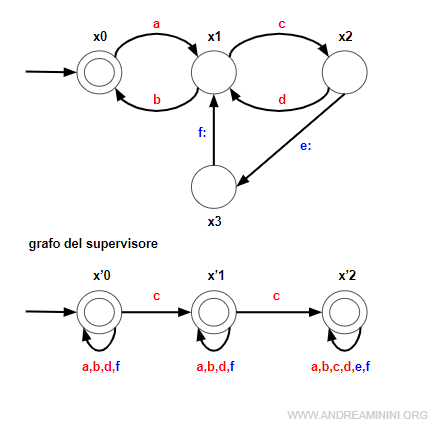
La supervisione totale e parziale
Il SED del supervisore ha un proprio insieme degli stati X', una propria funzione di transizione δ', un proprio stato inziale x'0 e un proprio insieme di stati finali X'm.
$$ S=(X',E, δ', x'_0, X'_m ) $$
L'alfabeto E è invece lo stesso dell'automa oppure un sottoinsieme E'⊆E.
Nell'esempio precedente il SED del supervisore utilizza tutto l'alfabeto E={a,b,c,d,e,f} dell'automa.
In questo caso si parla di supevisione totale.
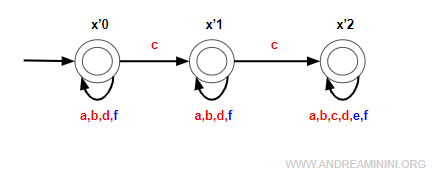
Posso rappresentare il supervisore anche usando un sottoinsieme E'={c,e} dell'alfabeto E.
In questo caso si parla di supervisione parziale, perché il supervisore lavora su un sottoinsieme del linguaggio L'⊆L dell'automa.
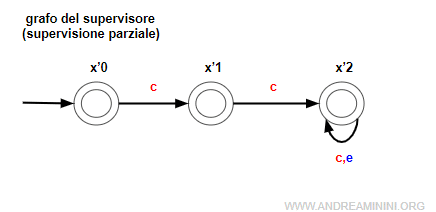
Il grafo del supervisore parziale replica soltanto gli eventi {c,e} mentre ignora tutti gli altri.
Nella supervisione parziale il SED del supervisore lavora su una proiezione di w sull'alfabeto parziale E'={c,e}.
| w | w↑E' | x' | ξ'(w) | ξ(w) |
|---|---|---|---|---|
| ε | ε | x'0 | ξ'(c) | ξ(abcdf) |
| a | ε | x'0 | ξ'(c) | ξ(abcdf) |
| ac | c | x'1 | ξ'(c) | ξ(abcdf) |
| acd | c | x'1 | ξ'(c) | ξ(abcdf) |
| acdc | cc | x'2 | ξ'(ce) | ξ(abcdef) |
| ... |
Nota. La supervisione sistema è molto più potente rispetto alla funzione di controllo f(w) perché permette di marcare alcune parole w del linguaggio L dell'automa con degli stati finali (ad esempio x'0, x'1, x'2). Altre parole w del linguaggio L sono invece ignorate (non marcate). Per questa ragione la supervisione sistema è detta marcante. Viceversa, la funzione di controllo f(w) è sempre non marcante perché considera tutte le parole w del linguaggio come singoli stati.
Il linguaggio
In un SED supervisionato (a ciclo chiuso) alcune sequenze di parole sono impedite dall'azione del supervisore.
Pertanto, il linguaggio generato da un SED a ciclo chiuso (supervisionato) L(S/P) è un sottoinsieme del linguaggio generato dallo stesso SED a ciclo aperto (non supervisionato) L(G).
$$ L(S/P) ⊆ L(P) $$
Dove P è il processo a ciclo aperto (SED non supervisionato) e S è il supervisore. Il simbolo S/P indica il SED P supervisionato da S.
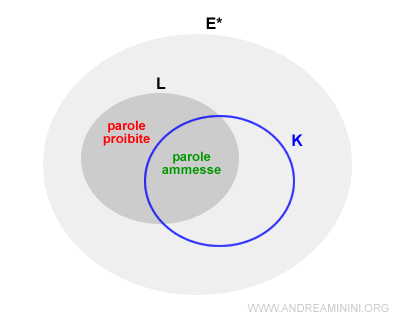
Il linguaggio accettato Lm dal sistema a ciclo chiuso S/P è l'intersezione tra i linguaggi accettati dl sistema P e dal sistema S.
$$ L_m(S/P) = L_m(S) ⋂ L_m(P) $$
Esempio. Una parola w seguita dall'evento s è indicata con il simbolo ws. La parola ws appartiene al linguaggio L(S/G) soltanto se la sequenza w appartiene al linguaggio L(S/G) e l'evento s è abilitato dal supervisore dopo w.
In un automa deterministico a stati finiti il linguaggio del sistema a ciclo chiuso S/P è determinato per composizione concorrente dei linguaggi P (processo) e S (supervisore).
Sia il linguaggio generato che il linguaggio accettato.
$$ L(S/P) = L(P) || L(S) $$
$$ L_m(S/P) = L_m(P) || L_m(S) $$
Esempio
In questo sistema è presente un processo P e un supervisore S.
Il supervisore abilita l'evento "e" dopo che si verifichi almeno due volte l'evento "c".
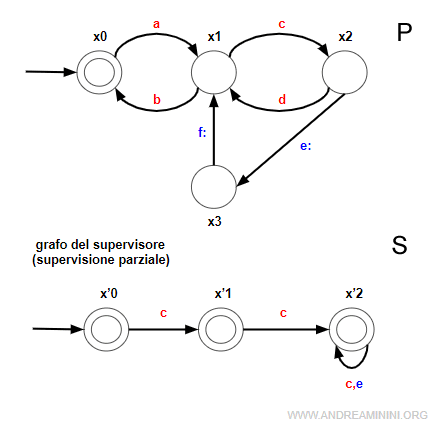
Si tratta di una supervisione parziale perché il supervisore usa soltanto un sottoinsieme di eventi ES={c,e} rispetto all'alfabeto EP={a,b,c,d,e,f} del processo.
L'unione dell'insieme dei simboli (alfabeto) del sistema è
$$ E = E_P ∪ E_S = \{ a,b,c,d,e,f \} $$
Utilizzo l'alfabeto E per generare delle parole (w).
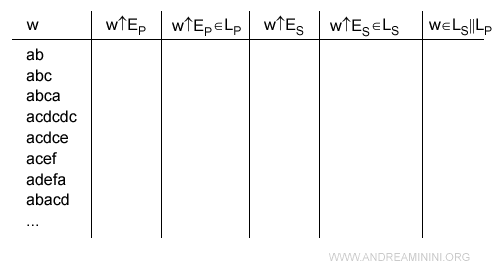
Calcolo le proiezioni delle parole w del linguaggio sugli alfabeti EP ed ES
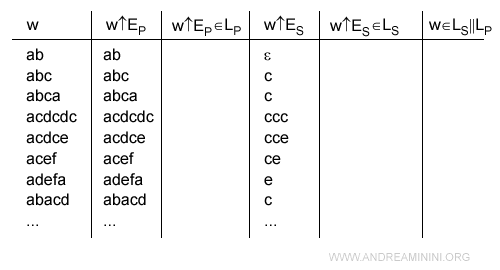
Poi verifico quali proiezioni w↑EP e w↑ES appartengono ai rispettivi linguaggi accettati LP e LS.
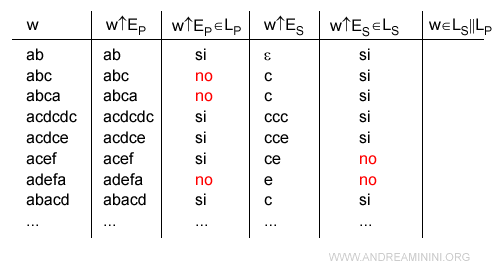
Nota. Le parole w↑EP∈LP sono le parole (w) del linguaggio accettato dal SED P a ciclo aperto (non supervisionato).
Le parole w che rispettano entrambe le condizioni appartengono alla composizione concorrente del linguaggio LP||LS.
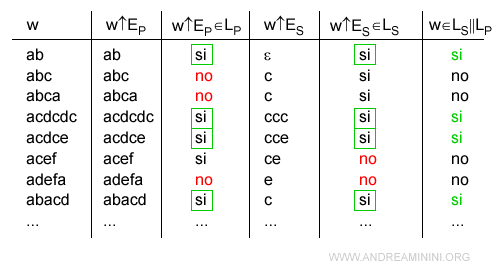
Sono le parole del linguaggio accettato dal sistema a ciclo chiuso S/P (supervisionato).
Esempio. La sequenza w=acdce è accettata dal sistema supervisionato S/P perché il supervisore abilita l'evento "e" dopo che si verifichi almeno due volte l'evento "c". Viceversa, la sequenza w=acef non è accettata dal sistema supervisionato S/P, pur facendo parte del linguaggio accettato del processo P, perché l'evento "e" non è abilitato dopo un solo evento "c".
E così via.
